广东省江门市新会区尚雅中学2022-2023学年八年级上学期第一次月考数学试题(无答案)

2022-2023学年度第一学期

八年级数学第一次大练习（B）

一、选择题（每小题3分，共30分）

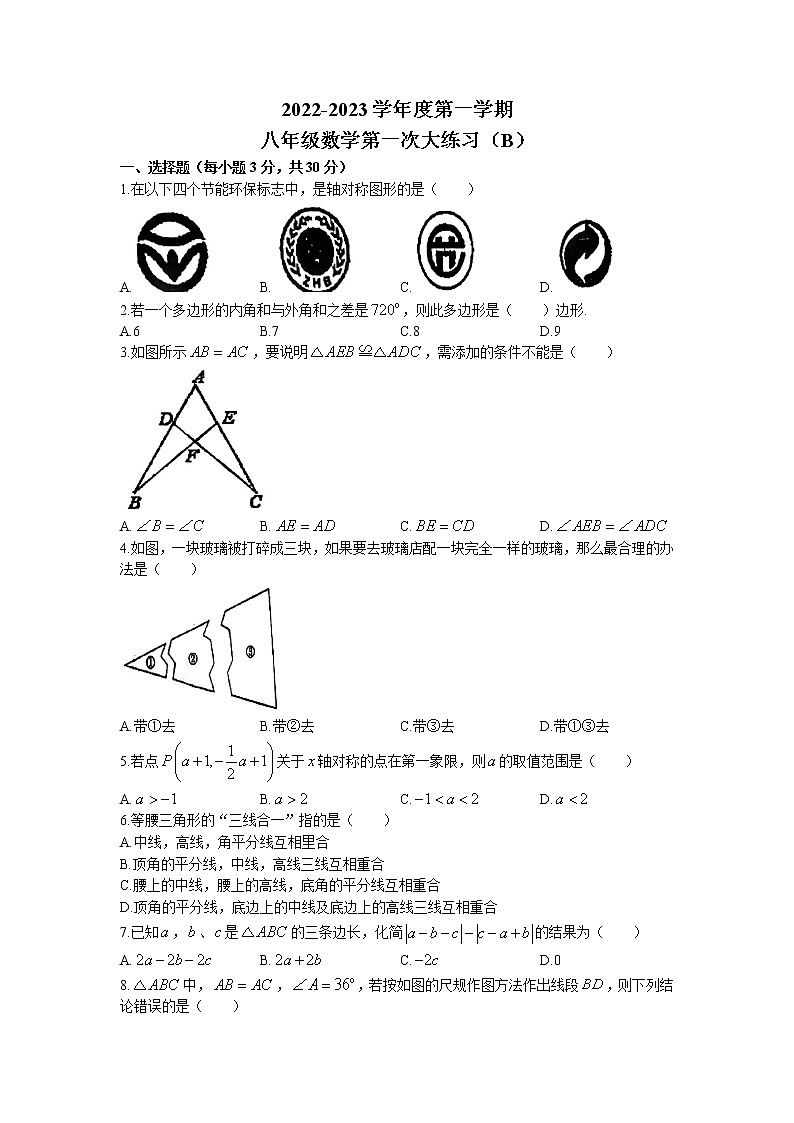
1.在以下四个节能环保标志中，是轴对称图形的是（    ）

A. B. C. D.

2.若一个多边形的内角和与外角和之差是，则此多边形是（    ）边形.

A.6 B.7 C.8 D.9

3.如图所示，要说明，需添加的条件不能是（    ）

A. B. C. D.

4.如图，一块玻璃被打碎成三块，如果要去玻璃店配一块完全一样的玻璃，那么最合理的办法是（    ）

A.带①去 B.带②去 C.带③去 D.带①③去

5.若点关于轴对称的点在第一象限，则的取值范围是（    ）

A. B. C. D.

6.等腰三角形的“三线合一”指的是（    ）

A.中线，高线，角平分线互相里合

B.顶角的平分线，中线，高线三线互相重合

C.腰上的中线，腰上的高线，底角的平分线互相重合

D.顶角的平分线，底边上的中线及底边上的高线三线互相重合

7.已知，、是的三条边长，化简的结果为（    ）

A. B. C. D.0

8.中，，，若按如图的尺规作图方法作出线段，则下列结论错误的是（    ）

A. B. C. D:

9.如图，在中，边的垂直平分线，分别与边和边交于点和点，边的垂直平分线，分别与边和边交于点和点，又的周长为16，且，则的长为（    ）

A.16 B.15 C.14 D.13

10.如图，在中，，是的角平分线，点在上，过点作于点，延长至点，使，连接交于点，平分，交的延长线于点，连接，，，若，则下列结论：

①；②；③；④.

其中正确的有（    ）

A.①②③ B.①②③④ C.①② D.①③④

二、填空题（每小题4分，共28分）

11.在中，，且，则的度数为________.

12.已知点关于轴的对称点的坐标为，则点的坐标为________.

13.已知等腰三角形一腰上的高线与另一层的夹角为，那么这个等腰三角形的顶角等于________.

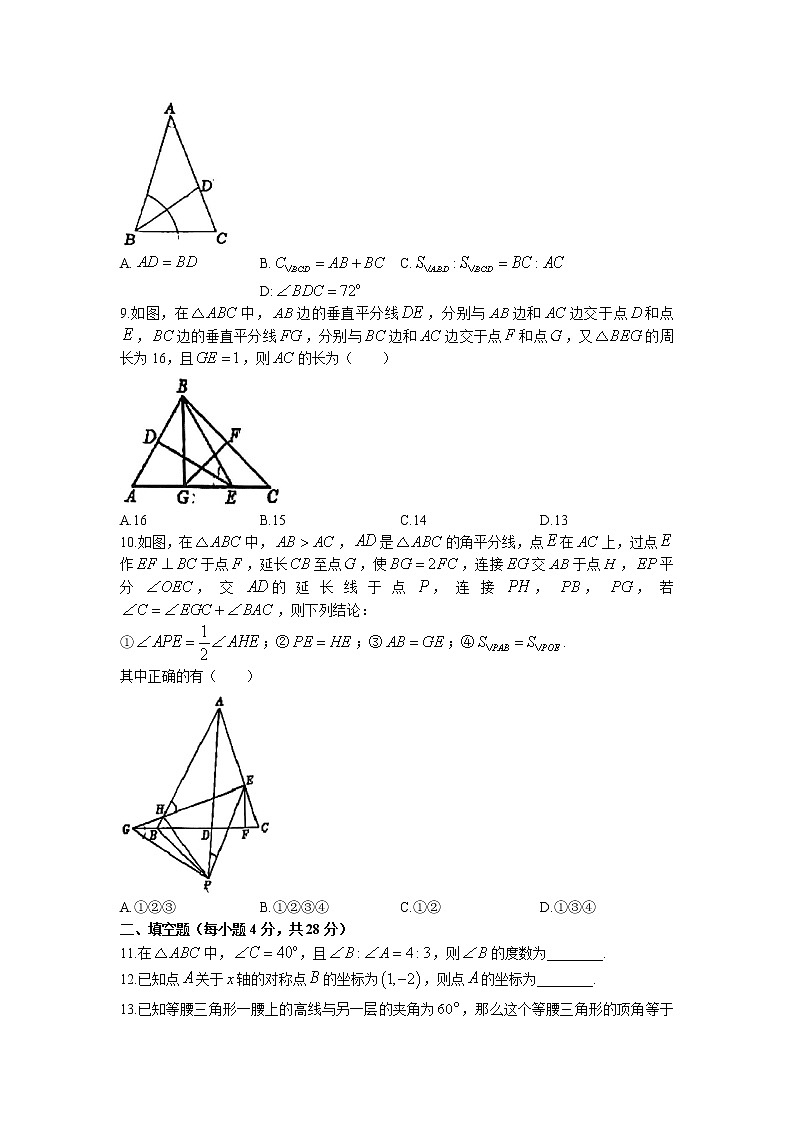
14.如图，在中，和的平分线交于点，过点作交于，交于，若，，，则的周长为________.

15.如图，在平面直角坐标系中，对进行循环往复的轴对称变换，若原来点坐标是，则经过第2022次变换后所得的点坐标是________.

16.如图，在中，，是的角平分线，已知，，，则的长为________.

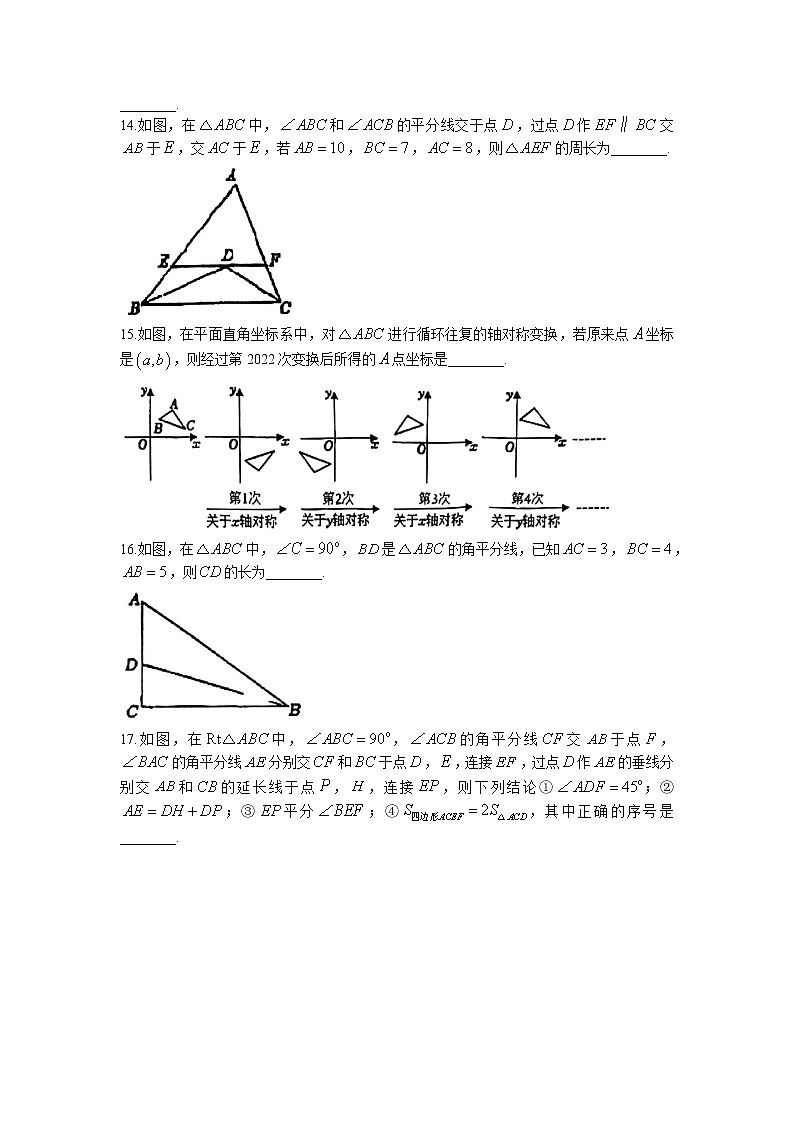
17.如图，在中，，的角平分线交于点，的角平分线分别交和于点，，连接，过点作的垂线分别交和的延长线于点，，连接，则下列结论①；②；③平分；④，其中正确的序号是________.

三、解答题（一）（每小题6分，共18分）

18.计算：

19.如图，在平面直角坐标系中，，，.

（1）在图中作出关于轴的对称图形，并写出点，，的坐标；

（2）求的面积.

20.如图，中，是它的角平分线，是上的一点，交与，交与.求证：到的距离与到的距离相等.

四、解答题（二）（每小题8分，共32分）

21.上午8时，一条船从海岛出发，以（海里/时，）的速度向正北航行，10时到达海岛处，从、望灯塔，测得，.求从海岛到灯塔的距离.

22.如图，在中，，用尺规作的垂直平分线，交鈄边于点.

（1）猜想：点是的什么特殊点？证明你的猜想；

（2）点在的垂直平分线上吗?说明理由；

（3）结合（1）（2），你有何发现?

23.4月23日为“世界读书日”，很多人管4月叫做“读书月”.为了营造书香校园，更好地进行读书月活动的开展，某校进行了问卷调查，对本校学生3月（共31天）的阅读总时间作了随机抽样分析．设被抽样的每位同学3月份阅读的总时间为t（小时），阅读总时间分为四个类别：，，，，将分类结果制成两幅统计图（尚不完整）.

根据以上信息，回答下列问题：

（1）本次被抽查到的学生总人数为________，扇形统计图中的值为________，圆心角的度数为________；

（2）补全条形统计图；

（3）若该校有3000名学生，估计3月份阅读的总时间小于24小时的学生约有多少名?对这些学生用一句话提一条阅读方面的建议.

24.随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为2000元、1700元的、两种型号的净水器，下表旲近两周的销售情况：

（1）型号净水器的销售单价为________，型号净水器的销售单价为________.

（2）若电器公司准备用不多于54000元的金额在乎购这两种型号的净水器共30台，求种型号的争水器最多的采购多少台?

（3）在（2）的条件下，公司销售完这30台净水器能否实现利润为12800元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

五、解答题（三）（每小题10分，共20分）

25.对于，，定义，若，则称与是关于1的“对称数”.

（1）填空：7与________是关于1的“对称数”与________是关于1的“对称数”

（2）若，，判断与是不是关于1的“对称数”，并说明理由

（3）已知，，其中，均为常数，且无论取何值，与都是关于1的“对称数”，求，的值；

26.

（1）如图1，已知，在中，，平分，平分，过点作，分别交、于、两点，则因中共有________个等腰三角形：与、之间的数量关系是________，的周长是________.

（2）如图2，若将（1）中“中，”改为“若为不等边三角形，，”其余条件不变，则图中共有________个等腰三角形；与、之间的数量关系是什么？证明你的结论，并求出的周长。

（3）已知：如图3，在外，，且平分，平分的外角，过点作，分别交、于、两点，则与、之间又有何数量关系呢？写出结论并证明.

六、解答题（四）（每小题12分，共12分）

27.如图，点为的外角的平分线上一点，，于点.

（1）求证:；

（2）若，，求；

（3）如图2，若，分别是边，上的点，且，求证：.