
还剩28页未读,
继续阅读
成套系列资料,整套一键下载
浙教版初中数学八年级上册第四单元《图形与坐标》单元测试卷(困难)(含答案解析)
展开
这是一份浙教版初中数学八年级上册第四单元《图形与坐标》单元测试卷(困难)(含答案解析),共31页。
浙教版初中数学八年级上册第四单元《图形与坐标》单元测试卷
考试范围:第四单元;考试时间:120分钟;分数:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,一个动点在第一象限内及x轴,y轴的正半轴上按一定的规律运动.在第一分钟时,它从原点运动到(1,0),第二分钟时从(1,0)运动到(1,1),然后它接着按图中箭头所示方向在与x轴,y轴平行的方向上来回运动,且每分钟移动1个单位.在第57 min结束时,这个动点所在位置的坐标是( )
A. (6,7) B. (7,0) C. (7,8) D. (8,0)
2. 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2021次相遇地点的坐标是( )
A. (2,0) B. (−1,1) C. (−2,1) D. (−1,−1)
3. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)⋯⋯根据这个规律,第2021个点的纵坐标为( )
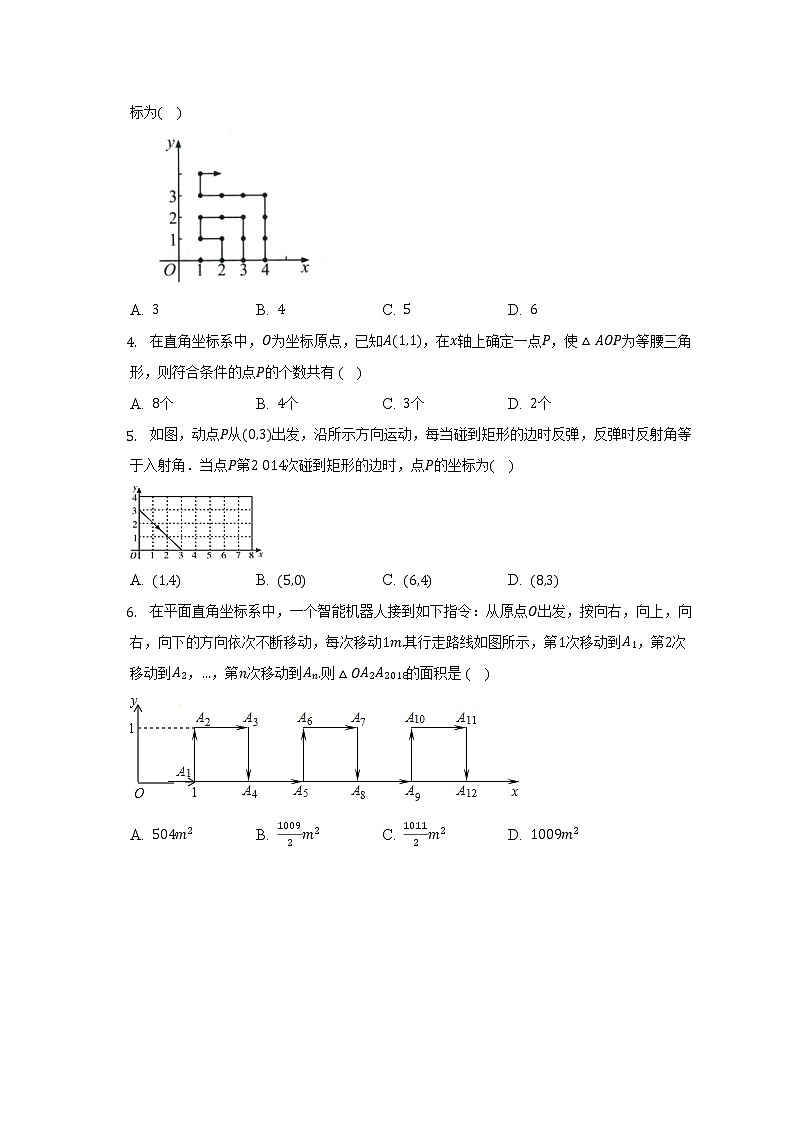
A. 3 B. 4 C. 5 D. 6
4. 在直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A. 8个 B. 4个 C. 3个 D. 2个
5. 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第2 014次碰到矩形的边时,点P的坐标为( )
A. (1,4) B. (5,0) C. (6,4) D. (8,3)
6. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )
A. 504m2 B. 10092m2 C. 10112m2 D. 1009m2
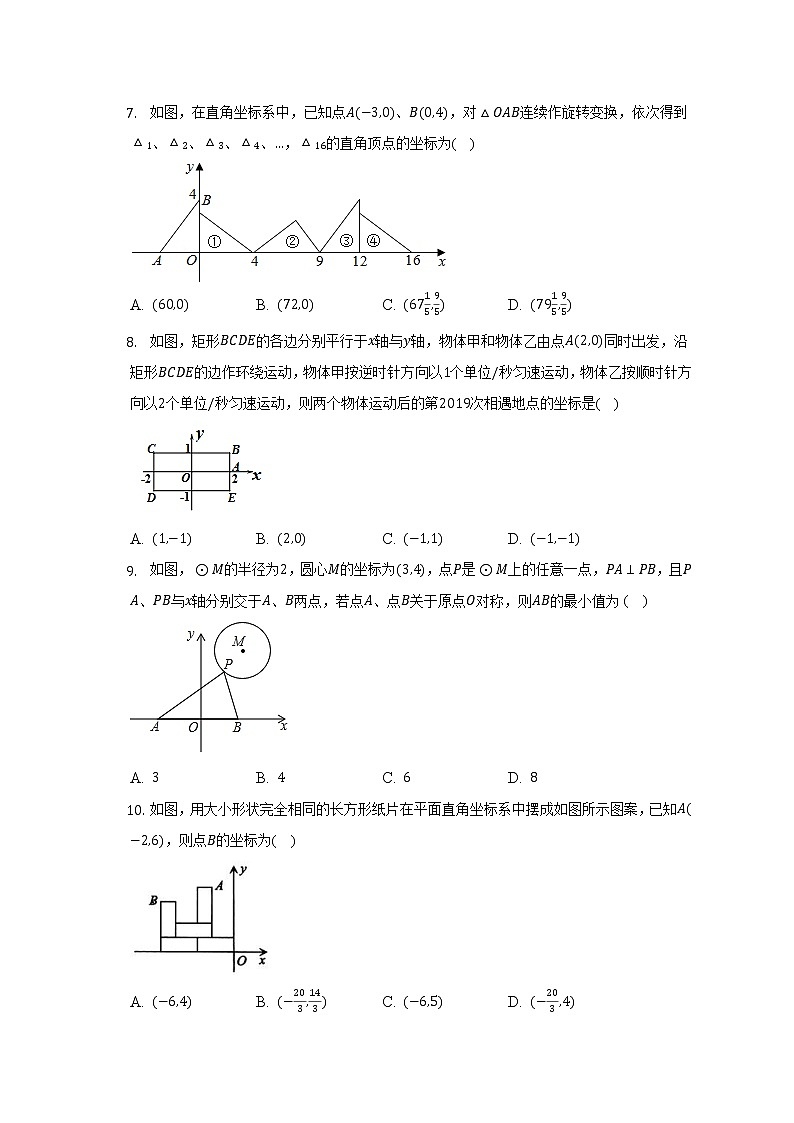
7. 如图,在直角坐标系中,已知点A(−3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
A. (60,0) B. (72,0) C. (6715,95) D. (7915,95)
8. 如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )
A. (1,−1) B. (2,0) C. (−1,1) D. (−1,−1)
9. 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A. 3 B. 4 C. 6 D. 8
10. 如图,用大小形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示图案,已知A(−2,6),则点B的坐标为( )
A. (−6,4) B. (−203,143) C. (−6,5) D. (−203,4)
11. 在平面直角坐标系中,点P(−2,3)关于x轴的对称点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
12. 如图,已知△ABC的三个顶点A(a,0),B(b,0),C(0,2a)b>a>0,作△ABC关于直线AC的对称图形△AB′C.若点B′恰好落在y轴上,则ab的值为( )
A. 13 B. 49 C. 12 D. 38
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13. 定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为点P、Q的“实际距离”.如图,若点P、Q的坐标分别为(−1,1)、(2,3),则点P、Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车正式成为市民出行喜欢的交通工具.设A、B、C三个小区的坐标分别为A(3,1)、B(5,−3)、C(−1,−5).若点M表示单车停放点,且满足点M到点A、B、C的“实际距离”相等,则点M的坐标为________.
14. 九年级某班有48名学生,所在教室有6行8列座位,用m,n表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为m,n,若调整后的座位为i,j,则称该生作了平移a,b=m−i,n−j,并称a+b为该生的位置数.若某生的位置数为9,则当m+n取最小值时,mn的最大值为 .
15. 如果P(m+3,2m+4)在y轴上,那么点P的坐标是___________.
16. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后动点P的坐标是____.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
我国法定节假日的确定为大家带来了很多便利、现在我们用坐标来表示下列这些节日:用A(1,1)表示元旦(即1月1日),用B(4,5)表示清明节(即4月5日),用C(6,1)表示儿童节(即6月1日),
(1)请写出教师节所对应的坐标D(______),国庆节所对应的坐标E(______);
(2)在右图坐标系中描出点A、B、C、D、E,并顺次连接AB、BC、CD、DE、EA;
(3)求出(2)中所画出的图形的面积.
18. (本小题8.0分)
天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.9h来估计,其中h(单位:m)是眼睛离海平面的高度.
(1)如果一个人站在岸边观察,当眼睛离海平面的高度是2.5m时,能看到多远?
(2)若登上一个观望台,使看到的最远距离是(1)中的3倍,已知眼睛到脚底的高度为1.5米,求观望台离海平面的高度?
(3)如图,货轮B与观望台A相距35海里,如何用方向和距离描述观望台A相对于货轮B的位置______.
19. (本小题8.0分)
国昌实验中学八年级合作学习小组的同学学习了全等三角形的概念后,聪明的正宇同学代表本小组给其他小组内的同学出了这样一个问题:在直角坐标系中,点A(−3,0),B(−1,0),C(−1,3),若有一个直角三角形与Rt△ABC全等,且它们只有一条公共直角边,这样的直角三角形有几个⋅若有,请写出第三个顶点的坐标.
20. (本小题8.0分)
在平面直角坐标系xOy中,已知O为坐标原点,点A(2,1),若△AOB为等腰直角三角形,求点B的坐标.
21. (本小题8.0分)
等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
22. (本小题8.0分)
在平面直角坐标系中,点A(0,a),B(2,b),C(4,0),且a>0.
(1)若(a−2)2+b−4=0,求点A,点B的坐标;
(2)如图,在(1)的条件下,过点B作BD平行y轴,交AC于点D,求点D的坐标;
(3)若S△ABC=5,且a+b−4=0,求b的值.
23. (本小题8.0分)
在平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(1)当⊙O的半径为2时,
①在点P1(12,0),P2(12,32),P3(52,0)中,⊙O的关联点是______ .
②点P在直线y=−x上,若P为⊙O的关联点,求点P的横坐标的取值范围.
(2)⊙C的圆心在x轴上,半径为2,直线y=−x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值范围.
24. (本小题8.0分)
在平面直角坐标系中,点A(0,5),B(12,0),在y轴负半轴上取点E,使OA=OE,作∠CEF=∠AEB,直线CO交BA的延长线于点D
(1)根据题意,可求得OE=______;
(2)求证:△ADO≌△ECO;
(3)动点P从点E出发,沿E—O—B路线运动,速度为每秒1个单位,到B点处停止运动;动点Q从B点出发,沿B—O—E运动,速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N,问两动点运动多长时间△OPM与△OQN全等?
25. (本小题8.0分)
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,B(10,4),点D是OA的中点,P是线段BC上一动点,当△ODP是等腰三角形时,求点P的坐标.
答案和解析
1.【答案】A
【解析】
【分析】
本题考查了点的坐标的变化规律,观察出点的个数按照平方数的规律变化是解题的关键.观察不难发现,点的个数按照平方数的规律变化,并且横坐标是奇数时按照运动
方向点的纵坐标变大,横坐标是奇数时,按照运动方向点的纵坐标变小,求出与57最接近的平方数,然后解答即可.
【解答】
解:第57分钟结束时,点运动的路程是57,
∵72=49,57−49=8,
∴第57分钟结束时的点为从点(7,0)开始运动的第8个点,
坐标为(6,7).
故选A.
2.【答案】D
【解析】
【分析】
此题主要考查了点的坐标变化规律以及行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.
利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
【解答】
解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×13=4,物体乙行的路程为12×23=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×13=8,物体乙行的路程为12×2×23=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×13=12,物体乙行的路程为12×3×23=24,在A点相遇;
此时甲、乙回到原出发点,则每相遇三次,两点回到出发点,
∵2021÷3=672······2,
∴两个物体运动后的第2021次相遇地点的是:第二次相遇地点,
即物体甲行的路程为12×2×13=8,物体乙行的路程为12×2×23=16,在DE边相遇;
此时相遇点的坐标为:(−1,−1).
故选D.
3.【答案】B
【解析】
【分析】根据点的坐标的变化可得出“第(2n−1)2个点的坐标为(2n−1,0)(n为正整数)”,依此规律可得出第2025个点的坐标为(45,0),再结合第2021个点在第2025个点的上方4个单位长度处,即可求出第2021个点的坐标,此题得解.
【解答】解:观察图形,可知:第1个点的坐标为(1,0),第4个点的坐标为(1,1),第9个点的坐标为(3,0),第16个点的坐标为(1,3),…,
∴第(2n−1)2个点的坐标为(2n−1,0)(n为正整数).
∵2025=45 2,
∴第2025个点的坐标为(45,0).
又∵2025−4=2021,
∴第2021个点在第2025个点的上方4个单位长度处,
∴第2021个点的坐标为(45,4).
故答案为:4.
本题考查了规律型:点的坐标,根据点的坐标的变化,找出变化规律“第(2n−1)2个点的坐标为(2n−1,0)(n为正整数)”是解题的关键.
4.【答案】B
【解析】
【分析】
此题考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.此题应该分情况讨论.以OA为腰或底分别讨论.当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有2个,若OA是底边时,P是OA的中垂线与x轴的交点,有1个,即可得.
【解答】
解:如图所示:
(1)若AO作为腰时,有两种情况,
①当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有1个,若OA是底边时,P是OA的中垂线与x轴的交点,有1个;
②当O是顶角顶点时,P是以O为圆心,以OA为半径的圆与x轴的交点,有2个;
(2)若OA是底边时,P是OA的中垂线与x轴的交点,有1个.
以上4个交点没有重合的.故符合条件的点有4个.
故选B.
5.【答案】B
【解析】
【分析】
本题考查的知识点是平面直角坐标系中点的坐标,用坐标描述位置,图形规律问题,首先根据反射角与入射角的定义作出图形,由图形规律可知每6次反弹为一个循环组依次循环,用2014除以6,根据商和余数的情况确定所对应的点的坐标即可.
【解答】
解:根据反射角与入射角的定义作出图形,
,
观察图形可知,经过6次反弹后动点回到出发点(0,3),
∵2 014÷6=335……4,
∴当点P第2 014次碰到矩形的边时为第336个循环组的第4次反弹,
∴点P的坐标为(5,0).
故选B.
6.【答案】A
【解析】
【分析】
本题主要考查点的坐标的变化规律,解题的关键是根据图形得出下标为4的倍数时对应长度即为下标的一半,据此可得.由OA4n=2n知OA2018=20162+1=1009,据此得出A2A2018=1009−1=1008,据此利用三角形的面积公式计算可得.
【解答】
解:由题意知OA4n=2n,
∵2018÷4=504÷2,
∴OA2018=20162+1=1009,
∴A2A2018=1009−1=1008,
则△OA2A2018的面积是12×1×1008=504m2,
故选A.
7.【答案】A
【解析】解:由题意可得,
△OAB旋转三次和原来的相对位置一样,点A(−3,0)、B(0,4),
∴OA=3,OB=4,∠BOA=90°,
∴AB=32+42=5
∴旋转到第三次时的直角顶点的坐标为:(12,0),
16÷3=5…1
∴旋转第15次的直角顶点的坐标为:(60,0),
又∵旋转第16次直角顶点的坐标与第15次一样,
∴旋转第16次的直角顶点的坐标是(60,0).
故选:A.
根据题目提供的信息,可知旋转三次为一个循环,图中第三次和第四次的直角顶点的坐标相同,由①→③时直角顶点的坐标可以求出来,从而可以解答本题.
本题考查规律性:点的坐标,解题的关键是可以发现其中的规律,利用发现的规律找出所求问题需要的条件.
8.【答案】B
【解析】
【分析】
此题主要考查了点的变化规律以及行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.解本题的关键是找出规律每相遇三次,甲乙两物体回到出发点.利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
【解答】
解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×13=4,物体乙行的路程为12×23=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×13=8,物体乙行的路程为12×2×23=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×13=12,物体乙行的路程为12×3×23=24,在A点相遇;
此时甲乙回到原出发点,
则每相遇三次,甲乙两物体回到出发点,
∵2019÷3=673,
∴两个物体运动后的第2019次相遇地点的是BE边相遇,且甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×13=12,物体乙行的路程为12×3×23=24,
此时相遇点的坐标为:A(2,0),
故选B.
9.【答案】C
【解析】
【分析】
本题主要考查直角三角形的性质,若要使AB取得最小值,则PO需取得最小值.连结OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,过点M作MQ⊥x轴于点Q,根据勾股定理可求解OM=5,进而求解AB=2OP′.
【解答】
解:∵PA⊥PB,
∴∠APB=90∘,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连结OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,过点M作MQ⊥x轴于点Q.
则OQ=3,MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6.
故选C.
10.【答案】B
【解析】
【分析】
本题考查了二元一次方程组的应用以及坐标与图形的性质,找准等量关系,正确列出二元一次方程组是解题的关键.设长方形纸片的长为x,宽为y,根据点A的坐标,即可得出关于x、y的二元一次方程组,解之即可得出x、y的值,再观察坐标系,可求出点B的坐标.
【解答】
解:设长方形的长为a,宽为b
则a−b=2a+2b=6
解得a=103b=43
∴−2a=−203,a+b=143,
∴点B的坐标为−203,143.
故选B.
11.【答案】C
【解析】解:点P(−2,3)关于x轴的对称点为(−2,−3),
(−2,−3)在第三象限.
故选:C.
首先根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得对称点的坐标,再根据坐标符号判断所在象限即可.
此题主要考查了关于x轴对称点的坐标特点,关键是掌握点的坐标的变化特点.
12.【答案】D
【解析】
【分析】
此题主要考查的角平分线的性质,勾股定理和三角形的面积.首先根据△ABC关于直线AC的对称图形△AB1C,若点B1恰好落在y轴上,求出OC=2a,OA=a,AB=b−a,BC=OC2+OB2=2a2+b2=4a2+b2,然后根据面积法得出OCCB=OAAB,再整理化简即可求出ab的值.
【解答】
解:过点A作AD⊥BC,垂足为D,
∵A(a,0)、B(b,0)、C(0,2a)(b>a>0),△ABC关于直线AC的对称图形△AB′C,点B′恰好落在y轴上,
∴OC=2a,OA=a,AB=b−a,BC=OC2+OB2=2a2+b2=4a2+b2,
∵AC平分∠OCB,AO⊥B′C,AD⊥BC,
∴AO=DA,
∴SΔAOCSΔABC=12CO×AO12BC×AD=COBC,
∵SΔAOCSΔABC=12AO×CO12AB×CO=AOAB,
∴OCCB=OAAB,
∴2a4a2+b2=ab−a,
整理化简得8a=3b,
∴ab=38,
故选D.
13.【答案】(1,−2)
【解析】
【分析】
此题主要考查了坐标确定位置等知识,正确理解实际距离的定义是解题关键.
若设M(x,y),构建方程组即可解决问题.
【解答】
解:设M(x,y),由“实际距离”的定义可知:
点M只能在ECFG区域内,
−1
∴|x−3|+|y−1|=|x−5|+|y+3|=|x+1|+|y+5|,①
∴|x−3|+1−y=5−x+|y+3|=x+1+y+5,②
要将|x−3|与|y+3|中绝对值去掉,
需要判断x在3的左侧和右侧,以及y在−3的上侧还是下侧,
将矩形ECFG分割为4部分,若要使M到A,B,C的距离相等,
由图可知M只能在矩形AENK中,
故x<3,y>−3,
则方程可变为:3−x+1−y=5−x+3+y=y+5+x+1,
解得,x=1,y=−2,
则M(1,−2).
故答案为(1,−2).
14.【答案】30
【解析】
【分析】
本题考查了新定义问题,坐标确定位置,二元一次方程的解以及代数式求值,解题关键是理解新定义“位置数”.
先由新定义结合a+b=9求出m+n的最小值为11,再由m、n为正整数确定m、n的值,进而得出mn的最大值.
【解答】
解:∵a,b=m−i,n−j,
∴a+b=m−i+n−j=m+n−(i+j),
又∵a+b=9,
∴m+n−i+j=9,即m+n=i+j+9,
∵1≤i≤6,1≤j≤8,且i、j都是整数,
∴m+n的最小值为11,
当m=3,n=8时,mn=24,
当m=4,n=7时,mn=28,
当m=5,n=6时,mn=30,
当m=6,n=5时,mn=30,
即mn的最大值为30.
故答案为30.
15.【答案】(0,−2)
【解析】
【分析】
解决本题的关键是掌握好坐标轴上的点的坐标的特征,y轴上的点的横坐标为0.
点P在y轴上则该点横坐标为0,可解得m的值,从而得到点P的坐标.
【解答】
解:∵P(m+3,2m+4)在y轴上,
∴m+3=0,得m=−3,
即2m+4=−2.即点P的坐标为(0,−2).
故答案为:(0,−2).
16.【答案】(2019,2)
【解析】
【分析】
本题是规律探究题,解题关键是找到动点运动过程中,每运动多少次形成一个循环.分析点P的运动规律,找到循环次数即可.
【解答】
解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.
∴2019=4×504+3
当第504循环结束时,点P位置在(2016,0),在此基础之上运动三次到(2019,2)
故答案为:(2019,2)
17.【答案】9,10 10,1
【解析】解:(1)根据规定,得
D(9,10),E(10,1).
(2)
(3)所求图形的面积=12×5×4+12×4×9=28.
(1)根据规定,知月份是点的横坐标,日期是点的纵坐标;
(2)根据点的坐标即可画图;
(3)结合图形,知图形的面积是两个三角形的面积,根据三角形的面积公式求解.
此题考查了描点的方法以及根据点的坐标求三角形的面积的方法,同时注意对生活常识的熟悉.
18.【答案】南偏西60方向,相距35海里
【解析】解:(1)当h=2.5时,s2=16.9×2.5=42.25,
∴s=−6.5(舍)或s=6.5,
答:当眼睛离海平面的高度是2.5m时,能看到6.5m远;
(2)当s=6.5×3=19.5时,可得19.52=16.9h,
解得h=22.5,
则观望台离海平面的高度为22.5−1.5=21米;
(3)观望台A在货轮B的南偏西60方向,相距35海里位置,
故答案为:南偏西60方向,相距35海里.
(1)求出h=2.5时s的值即可得;
(2)求出s=6.5×3=19.5时h的值,再减去1.5米即可得答案;
(3)根据方位角定义可得.
本题主要考查解一元二次方程和坐标确定位置,根据题意得出一元二次方程和方位角的定义是解题的关键.
19.【答案】解:如图.若以AB为公共边,则可以画3个直角三角形:△ABD、△ABE和△ABH.顶点D的坐标为(−1,−3),顶点E的坐标为(−3,3),顶点H的坐标为(−3,−3).
若以BC为公共边,则可以画3个直角三角形:△BCF、△BCE和△BCG.顶点F的坐标为(1,0),顶点E的坐标为(−3,3),顶点G的坐标为(1,3).
所以这样的直角三角形共有6个.
【解析】略
20.【答案】解:如解图,满足题意的点B的坐标为(1,−2)或(−1,2)或(3,−1)或(1,3)或32,−12或12,32.
【解析】
【分析】此题主要考查了坐标与图形,以及勾股定理逆定理的应用,关键是要分类讨论,不要漏解.首先画出坐标系,分别以O为直角顶点,B为直角顶点,A为直角顶点,利用坐标系找出B点坐标,注意要细心,不要漏解.
21.【答案】解:(1)过点C作CF⊥y轴于点F,
∴∠AFC=90°,
∴∠CAF+∠ACF=90°.
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AC=AB,∠CAF+∠BAO=90°,∠AFC=∠BAC,
∴∠ACF=∠BAO.
在△ACF和△BAO中,
∠AFC=∠BAC ∠ACF=∠BAO AC=AB,
∴△ACF≌△BAO(AAS),
∴CF=OA=1,AF=OB=2,
∴OF=1,
∴C(−1,−1);
(2)证明:过点C作CG⊥AC交y轴于点G,
∴∠ACG=∠BAC=90°,
∴∠AGC+∠GAC=90°.
∵∠CAG+∠BAO=90°,
∴∠AGC=∠BAO.
∵∠ADO+∠DAO=90°,∠DAO+∠BAO=90°,
∴∠ADO=∠BAO,
∴∠AGC=∠ADO.
在△ACG和△BAD中,
∠AGC=∠ADO ∠ACG=∠BAC AC=AB,
∴△ACG≌△BAD(AAS),
∴CG=AD=CD.
∵∠ACB=∠ABC=45°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
DC=GC∠DCE=∠GCECE=CE
∴△DCE≌△GCE(SAS),
∴∠CDE=∠CGE,
∴∠ADB=∠CDE;
(3)在OB上截取OH=OD,连接AH
由对称性得AD=AH,∠ADH=∠AHD.
∵∠ADH=∠BAO.
∴∠BAO=∠AHD.
∵BD是∠ABC的平分线,
∴∠ABO=∠EBO,
∵∠AOB=∠EOB=90°.
在△AOB和△EOB中,
∠ABO=∠EBO OB=OB ∠AOB=∠EOB,
∴△AOB≌△EOB(ASA),
∴AB=EB,AO=EO,
∴∠BAO=∠BEO,
∴∠AHD=∠ADH=∠BAO=∠BEO.
∴∠AEC=∠BHA.
在△AEC和△BHA中,
∠AEC=∠BHA ∠CAE=∠ABO AC=AB,
∴△ACE≌△BAH(AAS)
∴AE=BH=2OA,
∵DH=2OD,
∴BD=2(OA+OD).
【解析】本题考查了全等三角形的判定与性质的运用,等腰直角三角形的性质的运用,直角三角形的性质的运用,解答时证明三角形的全等是关键.
(1)过点C作CF⊥y轴于点F通过证△ACF≌△BAO得CF=OA=1,AF=OB=2,求得OF的值,就可以求出C的坐标;
(2)过点C作CG⊥AC交y轴于点G,先证明△ACG≌△BAD就可以得出CG=AD=CD,∠DCE=∠GCE=45°,再证明△DCE≌△GCE就可以得出结论;
(3)在OB上截取OH=OD,连接AH,由对称性得AD=AH,∠ADH=∠AHD,可证∠AHD=∠ADH=∠BAO=∠BEO,再证明△ACE≌△BAH就可以得出结论.
22.【答案】解:(1)∵(a−2)2+b−4=0,
∴a−2=0,且b−4=0,
∴a=2,b=4,
∴点A(0,2),B(2,4);
(2)连接OB,S△ABC=S△AOB+S△COB−S△AOC=12×2×2+12× 4×4−12×2×4=6,
设点D的坐标为(2,y),
S△ABC=S△ABD+ S△BCD=12(4−y)×2+12(4−y)×2=6,
∴y=1,即D(2,1).
或连接OD,S△AOD+S△COD=S△AOC=12×2×2+12×4×y= 12×2×4,
∴y=1,
∴D(2,1);
(3)分两种情况:
①点B在第一象限时,过B作BE//x轴,如下图1所示:
则BE⊥y轴,四边形OCBE是直角梯形,
∵S△ABC=直角梯形OCBE的面积−Rt△AOC的面积−△ABE的面积=5,
∴12(2+4)×b−12a×4−12×(b−a)×2=5,
整理得:2b−a=5,
∵a+b−4=0,
∴b=3;
②点B在第四象限时,过B作BE//x轴,过C作CF//AE,交直线BE于F,如下图2所示:
则BE⊥y轴,四边形ACFE是直角梯形,
∵S△ABC=直角梯形ACFE的面积−Rt△BCF的面积−△ABE的面积=5,
∴12(−b+a−b)×4−12(−b)×2−12×(a−b)×2=5,
整理得:a−2b=5,
∵a+b−4=0,
∴b=−13;
综上所述,若S△ABC=5,且a+b−4=0,b的值为3或−13.
【解析】本题考查了三角形的面积、偶次方和算术平方根的非负性质、坐标与图形性质、梯形面积公式、方程组的解法以及分类讨论等知识;本题综合性强,有一定难度.
(1)由偶次方和算术平方根的非负性质得出a−2=0,b−4=0,得出a=2,b=4,即可得出答案;
(2)根据题意可知点D为AC中点,即可得出点D的坐标.
(3)分两种情况讨论,由直角梯形的面积减去两个直角三角形的面积得出方程,即可得出答案.
23.【答案】解:(1)①P2,P3;
②根据定义分析,可得当y=−x上的点P到原点的距离在1到3之间时符合题意,
∴设P(x,−x),当OP=1时,
由距离公式得,OP=(x−0)2+(−x−0)2=1,
∴x=±22,
当OP=3时,OP=(x−0)2+(−x−0)2=3,
解得:x=±322;
∴点P的横坐标的取值范围为:−322≤x≤−22,或22≤x≤322;
(2)∵直线y=−x+1与x轴、y轴交于点A、B,
∴A(1,0),B(0,1),
如图1,
当圆过点A时,此时,CA=3,
∴C(−2,0),
如图2,
当直线AB与小圆相切时,切点为D,
∴CD=1,
∵直线AB的解析式为y=−x+1,
∴直线AB与x轴的夹角=45°,
∴AC=2,
∴C(1−2,0),
∴圆心C的横坐标的取值范围为:−2≤xC≤1−2;
如图3,
当圆过点O,则AC=1,∴C(2,0),
如图4,
当圆过点B,连接BC,此时,BC=3,
∴OC=32−1=22,
∴C(22,0).
∴圆心C的横坐标的取值范围为:2≤xC≤22;
综上所述;圆心C的横坐标的取值范围为:−2≤xC≤1−2或2≤xC≤22.
【解析】解:(1)①∵点P1(12,0),P2(12,32),P3(52,0),
∴OP1=12,OP2=1,OP3=52,
∴P1与⊙O的最小距离为32,P2与⊙O的最小距离为1,P3与⊙O的最小距离为12,
∴⊙O的关联点是P2,P3;
故答案为:P2,P3;
②见答案;
(2)(3)见答案。
(1)①根据点P1(12,0),P2(12,32),P3(52,0),求得OP1=12,OP2=1,OP3=52,于是得到结论;
②根据定义分析,可得当y=−x上的点P到原点的距离在1到3之间时符合题意,设P(x,−x),根据两点间的距离公式得到即可得到结论;
(2)根据已知条件得到A(1,0),B(0,1),如图1,当圆过点A时,得到C(−2,0),如图2,当直线AB与小圆相切时,切点为D,得到C(1−2,0),于是得到结论;如图3,当圆过点O,则AC=1,得到C(2,0),如图4,当圆过点B,连接BC,
根据勾股定理得到C(22,0),于是得到结论.
本题考查了一次函数的性质,勾股定理,直线与圆的位置关系,两点间的距离公式,正确的作出图形是解题的关键.
24.【答案】解:(1)5;
(2)证明:∵OE=OA,OB⊥AE,
∴BA=BE,
∴∠BAO=∠BEO.
∵∠CEF=∠AEB,
∴∠CEF=∠BAO,
∴EC//AB,
∴∠CEO=∠DAO.
在△ADO与△ECO中,
∠DAO=∠CEO,OA=OE,∠AOD=∠COE,
∴△ADO≌△ECO(ASA);
(3)设运动的时间为t秒,当PO=QO时,
易证△OPM≌△OQN.
①当点P、Q分别在y轴、x轴上时,PO=QO,
得:5−t=12−3t,
解得t=72;
②当点P、Q都在y轴上时PO=QO,
得:5−t=3t−12,
解得t=174;
③当点P在x轴上,Q在y轴上时,若二者都没有提前停止,
则PO=QO,
得:t−5=3t−12,
解得t=72,不合题意;
④当点Q运动到点E停止时PO=QO,
有t−5=5,
解得t=10.
综上所述:当两动点运动时间为72、174、10秒时,△OPM与△OQN全等.
【解析】
【分析】
本题考查了全等三角形的判定,坐标与图形的性质,正确的理解题意是解题的关键.
(1)根据题意,OE=OA即可求得;
(2)根据全等三角形的判定方法“ASA”证明△ADO≌△ECO;
(3)分类讨论:①当点P、Q分别在y轴、x轴上时PO=QO,求t;
②当点P、Q都在y轴上时PO=QO,求t;
③当点P在x轴上,Q在y轴上时PO=QO,若二者都没有提前停止,求t;
④当点Q运动到点E停止时PO=QO,求t.
【解答】
解:(1)根据题意,可求得OE=OA=5,
故答案为5;
(2)见答案;
(3)见答案.
25.【答案】解:∵四边形OABC是长方形,B(10,4),
∴OA=10,OC=4,
∵点D是OA的中点,
∴OD=5,
①当OD=OP=5时,在Rt△OPC中,OC=4,OP=5,由勾股定理可求得PC=3,此时P点坐标为(3,4);
②当OD=PD时,过P作PE⊥OA于点E,如图1,
在Rt△PED中,PE=OC=4,PD=5,
由勾股定理可求得DE=3,且OD=5,
则OE=5−3=2,
此时P点坐标为(2,4),(8,4);
根据已知条件及勾股定理计算得P2(2,4)或P3(8,4);
③当OP=PD时,点P为OD的垂直平分线与BC的交点,则P4(2.5,4).
综上可知,满足题意的点P的坐标为(3,4)或(2,4)或(8,4)或(2.5,4).
【解析】本题考查了坐标与图形的性质、等腰三角形的性质,正确分类讨论是解题关键.根据四边形OABC是长方形,B(10,4),点D是OA的中点,得OD=5,分OP=OD、PD=OD和PO=PD三种情况,结合坐标与图形的性质和勾股定理可求得P点的坐标.
浙教版初中数学八年级上册第四单元《图形与坐标》单元测试卷
考试范围:第四单元;考试时间:120分钟;分数:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,一个动点在第一象限内及x轴,y轴的正半轴上按一定的规律运动.在第一分钟时,它从原点运动到(1,0),第二分钟时从(1,0)运动到(1,1),然后它接着按图中箭头所示方向在与x轴,y轴平行的方向上来回运动,且每分钟移动1个单位.在第57 min结束时,这个动点所在位置的坐标是( )
A. (6,7) B. (7,0) C. (7,8) D. (8,0)
2. 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2021次相遇地点的坐标是( )
A. (2,0) B. (−1,1) C. (−2,1) D. (−1,−1)
3. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)⋯⋯根据这个规律,第2021个点的纵坐标为( )
A. 3 B. 4 C. 5 D. 6
4. 在直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A. 8个 B. 4个 C. 3个 D. 2个
5. 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第2 014次碰到矩形的边时,点P的坐标为( )
A. (1,4) B. (5,0) C. (6,4) D. (8,3)
6. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )
A. 504m2 B. 10092m2 C. 10112m2 D. 1009m2
7. 如图,在直角坐标系中,已知点A(−3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
A. (60,0) B. (72,0) C. (6715,95) D. (7915,95)
8. 如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2019次相遇地点的坐标是( )
A. (1,−1) B. (2,0) C. (−1,1) D. (−1,−1)
9. 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A. 3 B. 4 C. 6 D. 8
10. 如图,用大小形状完全相同的长方形纸片在平面直角坐标系中摆成如图所示图案,已知A(−2,6),则点B的坐标为( )
A. (−6,4) B. (−203,143) C. (−6,5) D. (−203,4)
11. 在平面直角坐标系中,点P(−2,3)关于x轴的对称点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
12. 如图,已知△ABC的三个顶点A(a,0),B(b,0),C(0,2a)b>a>0,作△ABC关于直线AC的对称图形△AB′C.若点B′恰好落在y轴上,则ab的值为( )
A. 13 B. 49 C. 12 D. 38
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13. 定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为点P、Q的“实际距离”.如图,若点P、Q的坐标分别为(−1,1)、(2,3),则点P、Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车正式成为市民出行喜欢的交通工具.设A、B、C三个小区的坐标分别为A(3,1)、B(5,−3)、C(−1,−5).若点M表示单车停放点,且满足点M到点A、B、C的“实际距离”相等,则点M的坐标为________.
14. 九年级某班有48名学生,所在教室有6行8列座位,用m,n表示第m行第n列的座位,新学期准备调整座位.设某个学生原来的座位为m,n,若调整后的座位为i,j,则称该生作了平移a,b=m−i,n−j,并称a+b为该生的位置数.若某生的位置数为9,则当m+n取最小值时,mn的最大值为 .
15. 如果P(m+3,2m+4)在y轴上,那么点P的坐标是___________.
16. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2019次运动后动点P的坐标是____.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
我国法定节假日的确定为大家带来了很多便利、现在我们用坐标来表示下列这些节日:用A(1,1)表示元旦(即1月1日),用B(4,5)表示清明节(即4月5日),用C(6,1)表示儿童节(即6月1日),
(1)请写出教师节所对应的坐标D(______),国庆节所对应的坐标E(______);
(2)在右图坐标系中描出点A、B、C、D、E,并顺次连接AB、BC、CD、DE、EA;
(3)求出(2)中所画出的图形的面积.
18. (本小题8.0分)
天气晴朗时,一个人能看到大海的最远距离s(单位:km)可用公式s2=16.9h来估计,其中h(单位:m)是眼睛离海平面的高度.
(1)如果一个人站在岸边观察,当眼睛离海平面的高度是2.5m时,能看到多远?
(2)若登上一个观望台,使看到的最远距离是(1)中的3倍,已知眼睛到脚底的高度为1.5米,求观望台离海平面的高度?
(3)如图,货轮B与观望台A相距35海里,如何用方向和距离描述观望台A相对于货轮B的位置______.
19. (本小题8.0分)
国昌实验中学八年级合作学习小组的同学学习了全等三角形的概念后,聪明的正宇同学代表本小组给其他小组内的同学出了这样一个问题:在直角坐标系中,点A(−3,0),B(−1,0),C(−1,3),若有一个直角三角形与Rt△ABC全等,且它们只有一条公共直角边,这样的直角三角形有几个⋅若有,请写出第三个顶点的坐标.
20. (本小题8.0分)
在平面直角坐标系xOy中,已知O为坐标原点,点A(2,1),若△AOB为等腰直角三角形,求点B的坐标.
21. (本小题8.0分)
等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
22. (本小题8.0分)
在平面直角坐标系中,点A(0,a),B(2,b),C(4,0),且a>0.
(1)若(a−2)2+b−4=0,求点A,点B的坐标;
(2)如图,在(1)的条件下,过点B作BD平行y轴,交AC于点D,求点D的坐标;
(3)若S△ABC=5,且a+b−4=0,求b的值.
23. (本小题8.0分)
在平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(1)当⊙O的半径为2时,
①在点P1(12,0),P2(12,32),P3(52,0)中,⊙O的关联点是______ .
②点P在直线y=−x上,若P为⊙O的关联点,求点P的横坐标的取值范围.
(2)⊙C的圆心在x轴上,半径为2,直线y=−x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值范围.
24. (本小题8.0分)
在平面直角坐标系中,点A(0,5),B(12,0),在y轴负半轴上取点E,使OA=OE,作∠CEF=∠AEB,直线CO交BA的延长线于点D
(1)根据题意,可求得OE=______;
(2)求证:△ADO≌△ECO;
(3)动点P从点E出发,沿E—O—B路线运动,速度为每秒1个单位,到B点处停止运动;动点Q从B点出发,沿B—O—E运动,速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N,问两动点运动多长时间△OPM与△OQN全等?
25. (本小题8.0分)
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,B(10,4),点D是OA的中点,P是线段BC上一动点,当△ODP是等腰三角形时,求点P的坐标.
答案和解析
1.【答案】A
【解析】
【分析】
本题考查了点的坐标的变化规律,观察出点的个数按照平方数的规律变化是解题的关键.观察不难发现,点的个数按照平方数的规律变化,并且横坐标是奇数时按照运动
方向点的纵坐标变大,横坐标是奇数时,按照运动方向点的纵坐标变小,求出与57最接近的平方数,然后解答即可.
【解答】
解:第57分钟结束时,点运动的路程是57,
∵72=49,57−49=8,
∴第57分钟结束时的点为从点(7,0)开始运动的第8个点,
坐标为(6,7).
故选A.
2.【答案】D
【解析】
【分析】
此题主要考查了点的坐标变化规律以及行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.
利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
【解答】
解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×13=4,物体乙行的路程为12×23=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×13=8,物体乙行的路程为12×2×23=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×13=12,物体乙行的路程为12×3×23=24,在A点相遇;
此时甲、乙回到原出发点,则每相遇三次,两点回到出发点,
∵2021÷3=672······2,
∴两个物体运动后的第2021次相遇地点的是:第二次相遇地点,
即物体甲行的路程为12×2×13=8,物体乙行的路程为12×2×23=16,在DE边相遇;
此时相遇点的坐标为:(−1,−1).
故选D.
3.【答案】B
【解析】
【分析】根据点的坐标的变化可得出“第(2n−1)2个点的坐标为(2n−1,0)(n为正整数)”,依此规律可得出第2025个点的坐标为(45,0),再结合第2021个点在第2025个点的上方4个单位长度处,即可求出第2021个点的坐标,此题得解.
【解答】解:观察图形,可知:第1个点的坐标为(1,0),第4个点的坐标为(1,1),第9个点的坐标为(3,0),第16个点的坐标为(1,3),…,
∴第(2n−1)2个点的坐标为(2n−1,0)(n为正整数).
∵2025=45 2,
∴第2025个点的坐标为(45,0).
又∵2025−4=2021,
∴第2021个点在第2025个点的上方4个单位长度处,
∴第2021个点的坐标为(45,4).
故答案为:4.
本题考查了规律型:点的坐标,根据点的坐标的变化,找出变化规律“第(2n−1)2个点的坐标为(2n−1,0)(n为正整数)”是解题的关键.
4.【答案】B
【解析】
【分析】
此题考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.此题应该分情况讨论.以OA为腰或底分别讨论.当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有2个,若OA是底边时,P是OA的中垂线与x轴的交点,有1个,即可得.
【解答】
解:如图所示:
(1)若AO作为腰时,有两种情况,
①当A是顶角顶点时,P是以A为圆心,以OA为半径的圆与x轴的交点,共有1个,若OA是底边时,P是OA的中垂线与x轴的交点,有1个;
②当O是顶角顶点时,P是以O为圆心,以OA为半径的圆与x轴的交点,有2个;
(2)若OA是底边时,P是OA的中垂线与x轴的交点,有1个.
以上4个交点没有重合的.故符合条件的点有4个.
故选B.
5.【答案】B
【解析】
【分析】
本题考查的知识点是平面直角坐标系中点的坐标,用坐标描述位置,图形规律问题,首先根据反射角与入射角的定义作出图形,由图形规律可知每6次反弹为一个循环组依次循环,用2014除以6,根据商和余数的情况确定所对应的点的坐标即可.
【解答】
解:根据反射角与入射角的定义作出图形,
,
观察图形可知,经过6次反弹后动点回到出发点(0,3),
∵2 014÷6=335……4,
∴当点P第2 014次碰到矩形的边时为第336个循环组的第4次反弹,
∴点P的坐标为(5,0).
故选B.
6.【答案】A
【解析】
【分析】
本题主要考查点的坐标的变化规律,解题的关键是根据图形得出下标为4的倍数时对应长度即为下标的一半,据此可得.由OA4n=2n知OA2018=20162+1=1009,据此得出A2A2018=1009−1=1008,据此利用三角形的面积公式计算可得.
【解答】
解:由题意知OA4n=2n,
∵2018÷4=504÷2,
∴OA2018=20162+1=1009,
∴A2A2018=1009−1=1008,
则△OA2A2018的面积是12×1×1008=504m2,
故选A.
7.【答案】A
【解析】解:由题意可得,
△OAB旋转三次和原来的相对位置一样,点A(−3,0)、B(0,4),
∴OA=3,OB=4,∠BOA=90°,
∴AB=32+42=5
∴旋转到第三次时的直角顶点的坐标为:(12,0),
16÷3=5…1
∴旋转第15次的直角顶点的坐标为:(60,0),
又∵旋转第16次直角顶点的坐标与第15次一样,
∴旋转第16次的直角顶点的坐标是(60,0).
故选:A.
根据题目提供的信息,可知旋转三次为一个循环,图中第三次和第四次的直角顶点的坐标相同,由①→③时直角顶点的坐标可以求出来,从而可以解答本题.
本题考查规律性:点的坐标,解题的关键是可以发现其中的规律,利用发现的规律找出所求问题需要的条件.
8.【答案】B
【解析】
【分析】
此题主要考查了点的变化规律以及行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.解本题的关键是找出规律每相遇三次,甲乙两物体回到出发点.利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.
【解答】
解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:
①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×13=4,物体乙行的路程为12×23=8,在BC边相遇;
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×13=8,物体乙行的路程为12×2×23=16,在DE边相遇;
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×13=12,物体乙行的路程为12×3×23=24,在A点相遇;
此时甲乙回到原出发点,
则每相遇三次,甲乙两物体回到出发点,
∵2019÷3=673,
∴两个物体运动后的第2019次相遇地点的是BE边相遇,且甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×13=12,物体乙行的路程为12×3×23=24,
此时相遇点的坐标为:A(2,0),
故选B.
9.【答案】C
【解析】
【分析】
本题主要考查直角三角形的性质,若要使AB取得最小值,则PO需取得最小值.连结OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,过点M作MQ⊥x轴于点Q,根据勾股定理可求解OM=5,进而求解AB=2OP′.
【解答】
解:∵PA⊥PB,
∴∠APB=90∘,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连结OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,过点M作MQ⊥x轴于点Q.
则OQ=3,MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6.
故选C.
10.【答案】B
【解析】
【分析】
本题考查了二元一次方程组的应用以及坐标与图形的性质,找准等量关系,正确列出二元一次方程组是解题的关键.设长方形纸片的长为x,宽为y,根据点A的坐标,即可得出关于x、y的二元一次方程组,解之即可得出x、y的值,再观察坐标系,可求出点B的坐标.
【解答】
解:设长方形的长为a,宽为b
则a−b=2a+2b=6
解得a=103b=43
∴−2a=−203,a+b=143,
∴点B的坐标为−203,143.
故选B.
11.【答案】C
【解析】解:点P(−2,3)关于x轴的对称点为(−2,−3),
(−2,−3)在第三象限.
故选:C.
首先根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得对称点的坐标,再根据坐标符号判断所在象限即可.
此题主要考查了关于x轴对称点的坐标特点,关键是掌握点的坐标的变化特点.
12.【答案】D
【解析】
【分析】
此题主要考查的角平分线的性质,勾股定理和三角形的面积.首先根据△ABC关于直线AC的对称图形△AB1C,若点B1恰好落在y轴上,求出OC=2a,OA=a,AB=b−a,BC=OC2+OB2=2a2+b2=4a2+b2,然后根据面积法得出OCCB=OAAB,再整理化简即可求出ab的值.
【解答】
解:过点A作AD⊥BC,垂足为D,
∵A(a,0)、B(b,0)、C(0,2a)(b>a>0),△ABC关于直线AC的对称图形△AB′C,点B′恰好落在y轴上,
∴OC=2a,OA=a,AB=b−a,BC=OC2+OB2=2a2+b2=4a2+b2,
∵AC平分∠OCB,AO⊥B′C,AD⊥BC,
∴AO=DA,
∴SΔAOCSΔABC=12CO×AO12BC×AD=COBC,
∵SΔAOCSΔABC=12AO×CO12AB×CO=AOAB,
∴OCCB=OAAB,
∴2a4a2+b2=ab−a,
整理化简得8a=3b,
∴ab=38,
故选D.
13.【答案】(1,−2)
【解析】
【分析】
此题主要考查了坐标确定位置等知识,正确理解实际距离的定义是解题关键.
若设M(x,y),构建方程组即可解决问题.
【解答】
解:设M(x,y),由“实际距离”的定义可知:
点M只能在ECFG区域内,
−1
∴|x−3|+|y−1|=|x−5|+|y+3|=|x+1|+|y+5|,①
∴|x−3|+1−y=5−x+|y+3|=x+1+y+5,②
要将|x−3|与|y+3|中绝对值去掉,
需要判断x在3的左侧和右侧,以及y在−3的上侧还是下侧,
将矩形ECFG分割为4部分,若要使M到A,B,C的距离相等,
由图可知M只能在矩形AENK中,
故x<3,y>−3,
则方程可变为:3−x+1−y=5−x+3+y=y+5+x+1,
解得,x=1,y=−2,
则M(1,−2).
故答案为(1,−2).
14.【答案】30
【解析】
【分析】
本题考查了新定义问题,坐标确定位置,二元一次方程的解以及代数式求值,解题关键是理解新定义“位置数”.
先由新定义结合a+b=9求出m+n的最小值为11,再由m、n为正整数确定m、n的值,进而得出mn的最大值.
【解答】
解:∵a,b=m−i,n−j,
∴a+b=m−i+n−j=m+n−(i+j),
又∵a+b=9,
∴m+n−i+j=9,即m+n=i+j+9,
∵1≤i≤6,1≤j≤8,且i、j都是整数,
∴m+n的最小值为11,
当m=3,n=8时,mn=24,
当m=4,n=7时,mn=28,
当m=5,n=6时,mn=30,
当m=6,n=5时,mn=30,
即mn的最大值为30.
故答案为30.
15.【答案】(0,−2)
【解析】
【分析】
解决本题的关键是掌握好坐标轴上的点的坐标的特征,y轴上的点的横坐标为0.
点P在y轴上则该点横坐标为0,可解得m的值,从而得到点P的坐标.
【解答】
解:∵P(m+3,2m+4)在y轴上,
∴m+3=0,得m=−3,
即2m+4=−2.即点P的坐标为(0,−2).
故答案为:(0,−2).
16.【答案】(2019,2)
【解析】
【分析】
本题是规律探究题,解题关键是找到动点运动过程中,每运动多少次形成一个循环.分析点P的运动规律,找到循环次数即可.
【解答】
解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.
∴2019=4×504+3
当第504循环结束时,点P位置在(2016,0),在此基础之上运动三次到(2019,2)
故答案为:(2019,2)
17.【答案】9,10 10,1
【解析】解:(1)根据规定,得
D(9,10),E(10,1).
(2)
(3)所求图形的面积=12×5×4+12×4×9=28.
(1)根据规定,知月份是点的横坐标,日期是点的纵坐标;
(2)根据点的坐标即可画图;
(3)结合图形,知图形的面积是两个三角形的面积,根据三角形的面积公式求解.
此题考查了描点的方法以及根据点的坐标求三角形的面积的方法,同时注意对生活常识的熟悉.
18.【答案】南偏西60方向,相距35海里
【解析】解:(1)当h=2.5时,s2=16.9×2.5=42.25,
∴s=−6.5(舍)或s=6.5,
答:当眼睛离海平面的高度是2.5m时,能看到6.5m远;
(2)当s=6.5×3=19.5时,可得19.52=16.9h,
解得h=22.5,
则观望台离海平面的高度为22.5−1.5=21米;
(3)观望台A在货轮B的南偏西60方向,相距35海里位置,
故答案为:南偏西60方向,相距35海里.
(1)求出h=2.5时s的值即可得;
(2)求出s=6.5×3=19.5时h的值,再减去1.5米即可得答案;
(3)根据方位角定义可得.
本题主要考查解一元二次方程和坐标确定位置,根据题意得出一元二次方程和方位角的定义是解题的关键.
19.【答案】解:如图.若以AB为公共边,则可以画3个直角三角形:△ABD、△ABE和△ABH.顶点D的坐标为(−1,−3),顶点E的坐标为(−3,3),顶点H的坐标为(−3,−3).
若以BC为公共边,则可以画3个直角三角形:△BCF、△BCE和△BCG.顶点F的坐标为(1,0),顶点E的坐标为(−3,3),顶点G的坐标为(1,3).
所以这样的直角三角形共有6个.
【解析】略
20.【答案】解:如解图,满足题意的点B的坐标为(1,−2)或(−1,2)或(3,−1)或(1,3)或32,−12或12,32.
【解析】
【分析】此题主要考查了坐标与图形,以及勾股定理逆定理的应用,关键是要分类讨论,不要漏解.首先画出坐标系,分别以O为直角顶点,B为直角顶点,A为直角顶点,利用坐标系找出B点坐标,注意要细心,不要漏解.
21.【答案】解:(1)过点C作CF⊥y轴于点F,
∴∠AFC=90°,
∴∠CAF+∠ACF=90°.
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AC=AB,∠CAF+∠BAO=90°,∠AFC=∠BAC,
∴∠ACF=∠BAO.
在△ACF和△BAO中,
∠AFC=∠BAC ∠ACF=∠BAO AC=AB,
∴△ACF≌△BAO(AAS),
∴CF=OA=1,AF=OB=2,
∴OF=1,
∴C(−1,−1);
(2)证明:过点C作CG⊥AC交y轴于点G,
∴∠ACG=∠BAC=90°,
∴∠AGC+∠GAC=90°.
∵∠CAG+∠BAO=90°,
∴∠AGC=∠BAO.
∵∠ADO+∠DAO=90°,∠DAO+∠BAO=90°,
∴∠ADO=∠BAO,
∴∠AGC=∠ADO.
在△ACG和△BAD中,
∠AGC=∠ADO ∠ACG=∠BAC AC=AB,
∴△ACG≌△BAD(AAS),
∴CG=AD=CD.
∵∠ACB=∠ABC=45°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
DC=GC∠DCE=∠GCECE=CE
∴△DCE≌△GCE(SAS),
∴∠CDE=∠CGE,
∴∠ADB=∠CDE;
(3)在OB上截取OH=OD,连接AH
由对称性得AD=AH,∠ADH=∠AHD.
∵∠ADH=∠BAO.
∴∠BAO=∠AHD.
∵BD是∠ABC的平分线,
∴∠ABO=∠EBO,
∵∠AOB=∠EOB=90°.
在△AOB和△EOB中,
∠ABO=∠EBO OB=OB ∠AOB=∠EOB,
∴△AOB≌△EOB(ASA),
∴AB=EB,AO=EO,
∴∠BAO=∠BEO,
∴∠AHD=∠ADH=∠BAO=∠BEO.
∴∠AEC=∠BHA.
在△AEC和△BHA中,
∠AEC=∠BHA ∠CAE=∠ABO AC=AB,
∴△ACE≌△BAH(AAS)
∴AE=BH=2OA,
∵DH=2OD,
∴BD=2(OA+OD).
【解析】本题考查了全等三角形的判定与性质的运用,等腰直角三角形的性质的运用,直角三角形的性质的运用,解答时证明三角形的全等是关键.
(1)过点C作CF⊥y轴于点F通过证△ACF≌△BAO得CF=OA=1,AF=OB=2,求得OF的值,就可以求出C的坐标;
(2)过点C作CG⊥AC交y轴于点G,先证明△ACG≌△BAD就可以得出CG=AD=CD,∠DCE=∠GCE=45°,再证明△DCE≌△GCE就可以得出结论;
(3)在OB上截取OH=OD,连接AH,由对称性得AD=AH,∠ADH=∠AHD,可证∠AHD=∠ADH=∠BAO=∠BEO,再证明△ACE≌△BAH就可以得出结论.
22.【答案】解:(1)∵(a−2)2+b−4=0,
∴a−2=0,且b−4=0,
∴a=2,b=4,
∴点A(0,2),B(2,4);
(2)连接OB,S△ABC=S△AOB+S△COB−S△AOC=12×2×2+12× 4×4−12×2×4=6,
设点D的坐标为(2,y),
S△ABC=S△ABD+ S△BCD=12(4−y)×2+12(4−y)×2=6,
∴y=1,即D(2,1).
或连接OD,S△AOD+S△COD=S△AOC=12×2×2+12×4×y= 12×2×4,
∴y=1,
∴D(2,1);
(3)分两种情况:
①点B在第一象限时,过B作BE//x轴,如下图1所示:
则BE⊥y轴,四边形OCBE是直角梯形,
∵S△ABC=直角梯形OCBE的面积−Rt△AOC的面积−△ABE的面积=5,
∴12(2+4)×b−12a×4−12×(b−a)×2=5,
整理得:2b−a=5,
∵a+b−4=0,
∴b=3;
②点B在第四象限时,过B作BE//x轴,过C作CF//AE,交直线BE于F,如下图2所示:
则BE⊥y轴,四边形ACFE是直角梯形,
∵S△ABC=直角梯形ACFE的面积−Rt△BCF的面积−△ABE的面积=5,
∴12(−b+a−b)×4−12(−b)×2−12×(a−b)×2=5,
整理得:a−2b=5,
∵a+b−4=0,
∴b=−13;
综上所述,若S△ABC=5,且a+b−4=0,b的值为3或−13.
【解析】本题考查了三角形的面积、偶次方和算术平方根的非负性质、坐标与图形性质、梯形面积公式、方程组的解法以及分类讨论等知识;本题综合性强,有一定难度.
(1)由偶次方和算术平方根的非负性质得出a−2=0,b−4=0,得出a=2,b=4,即可得出答案;
(2)根据题意可知点D为AC中点,即可得出点D的坐标.
(3)分两种情况讨论,由直角梯形的面积减去两个直角三角形的面积得出方程,即可得出答案.
23.【答案】解:(1)①P2,P3;
②根据定义分析,可得当y=−x上的点P到原点的距离在1到3之间时符合题意,
∴设P(x,−x),当OP=1时,
由距离公式得,OP=(x−0)2+(−x−0)2=1,
∴x=±22,
当OP=3时,OP=(x−0)2+(−x−0)2=3,
解得:x=±322;
∴点P的横坐标的取值范围为:−322≤x≤−22,或22≤x≤322;
(2)∵直线y=−x+1与x轴、y轴交于点A、B,
∴A(1,0),B(0,1),
如图1,
当圆过点A时,此时,CA=3,
∴C(−2,0),
如图2,
当直线AB与小圆相切时,切点为D,
∴CD=1,
∵直线AB的解析式为y=−x+1,
∴直线AB与x轴的夹角=45°,
∴AC=2,
∴C(1−2,0),
∴圆心C的横坐标的取值范围为:−2≤xC≤1−2;
如图3,
当圆过点O,则AC=1,∴C(2,0),
如图4,
当圆过点B,连接BC,此时,BC=3,
∴OC=32−1=22,
∴C(22,0).
∴圆心C的横坐标的取值范围为:2≤xC≤22;
综上所述;圆心C的横坐标的取值范围为:−2≤xC≤1−2或2≤xC≤22.
【解析】解:(1)①∵点P1(12,0),P2(12,32),P3(52,0),
∴OP1=12,OP2=1,OP3=52,
∴P1与⊙O的最小距离为32,P2与⊙O的最小距离为1,P3与⊙O的最小距离为12,
∴⊙O的关联点是P2,P3;
故答案为:P2,P3;
②见答案;
(2)(3)见答案。
(1)①根据点P1(12,0),P2(12,32),P3(52,0),求得OP1=12,OP2=1,OP3=52,于是得到结论;
②根据定义分析,可得当y=−x上的点P到原点的距离在1到3之间时符合题意,设P(x,−x),根据两点间的距离公式得到即可得到结论;
(2)根据已知条件得到A(1,0),B(0,1),如图1,当圆过点A时,得到C(−2,0),如图2,当直线AB与小圆相切时,切点为D,得到C(1−2,0),于是得到结论;如图3,当圆过点O,则AC=1,得到C(2,0),如图4,当圆过点B,连接BC,
根据勾股定理得到C(22,0),于是得到结论.
本题考查了一次函数的性质,勾股定理,直线与圆的位置关系,两点间的距离公式,正确的作出图形是解题的关键.
24.【答案】解:(1)5;
(2)证明:∵OE=OA,OB⊥AE,
∴BA=BE,
∴∠BAO=∠BEO.
∵∠CEF=∠AEB,
∴∠CEF=∠BAO,
∴EC//AB,
∴∠CEO=∠DAO.
在△ADO与△ECO中,
∠DAO=∠CEO,OA=OE,∠AOD=∠COE,
∴△ADO≌△ECO(ASA);
(3)设运动的时间为t秒,当PO=QO时,
易证△OPM≌△OQN.
①当点P、Q分别在y轴、x轴上时,PO=QO,
得:5−t=12−3t,
解得t=72;
②当点P、Q都在y轴上时PO=QO,
得:5−t=3t−12,
解得t=174;
③当点P在x轴上,Q在y轴上时,若二者都没有提前停止,
则PO=QO,
得:t−5=3t−12,
解得t=72,不合题意;
④当点Q运动到点E停止时PO=QO,
有t−5=5,
解得t=10.
综上所述:当两动点运动时间为72、174、10秒时,△OPM与△OQN全等.
【解析】
【分析】
本题考查了全等三角形的判定,坐标与图形的性质,正确的理解题意是解题的关键.
(1)根据题意,OE=OA即可求得;
(2)根据全等三角形的判定方法“ASA”证明△ADO≌△ECO;
(3)分类讨论:①当点P、Q分别在y轴、x轴上时PO=QO,求t;
②当点P、Q都在y轴上时PO=QO,求t;
③当点P在x轴上,Q在y轴上时PO=QO,若二者都没有提前停止,求t;
④当点Q运动到点E停止时PO=QO,求t.
【解答】
解:(1)根据题意,可求得OE=OA=5,
故答案为5;
(2)见答案;
(3)见答案.
25.【答案】解:∵四边形OABC是长方形,B(10,4),
∴OA=10,OC=4,
∵点D是OA的中点,
∴OD=5,
①当OD=OP=5时,在Rt△OPC中,OC=4,OP=5,由勾股定理可求得PC=3,此时P点坐标为(3,4);
②当OD=PD时,过P作PE⊥OA于点E,如图1,
在Rt△PED中,PE=OC=4,PD=5,
由勾股定理可求得DE=3,且OD=5,
则OE=5−3=2,
此时P点坐标为(2,4),(8,4);
根据已知条件及勾股定理计算得P2(2,4)或P3(8,4);
③当OP=PD时,点P为OD的垂直平分线与BC的交点,则P4(2.5,4).
综上可知,满足题意的点P的坐标为(3,4)或(2,4)或(8,4)或(2.5,4).
【解析】本题考查了坐标与图形的性质、等腰三角形的性质,正确分类讨论是解题关键.根据四边形OABC是长方形,B(10,4),点D是OA的中点,得OD=5,分OP=OD、PD=OD和PO=PD三种情况,结合坐标与图形的性质和勾股定理可求得P点的坐标.
相关资料
更多









