浙教版初中数学八年级上册期末测试卷（较易）（含答案解析）

浙教版初中数学八年级上册期末测试卷

考试范围：全册；考试时间：120分钟；分数：120分

学校:___________姓名：___________班级：___________考号：___________

第I卷（选择题）

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1.    如图，与相交于点，，，不添加辅助线，判定的依据是(    )
    

A.
B.
C.
D.

2.    如图是作的作图痕迹，则此作图的已知条件是(    )
    

A. 已知两边及夹角 B. 已知三边
C. 已知两角及夹边 D. 已知两边及一边对角

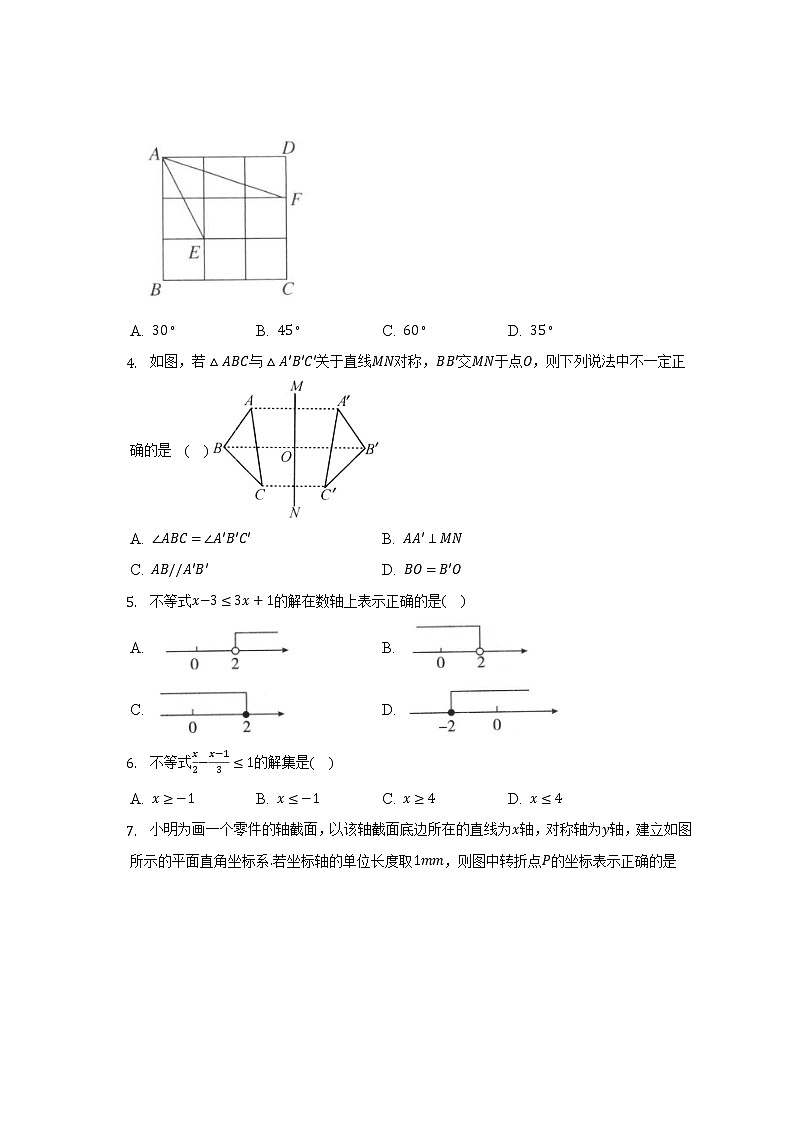
3.    如图，正方形是由个边长为的小正方形组成的，每个小正方形的顶点都叫格点，连结，，则的度数为(    )
   
    

A.  B.  C.  D.

4.    如图，若与关于直线对称，交于点，则下列说法中不一定正确的是  (    )

A.  B.
C.  D.

5.    不等式的解在数轴上表示正确的是(    )

A.  B.
C.  D.

6.    不等式的解集是(    )

A.  B.  C.  D.

7.    小明为画一个零件的轴截面，以该轴截面底边所在的直线为轴，对称轴为轴，建立如图所示的平面直角坐标系若坐标轴的单位长度取，则图中转折点的坐标表示正确的是(    )
    

A.  B.  C.  D.

8.    在平面直角坐标系中，点到轴的距离(    )

A.  B.  C.  D.

9.    已知直线过点和点，则和的大小关系是(    )

A.  B.  C.  D. 不能确定

10. 若是正比例函数，则的值是(    )

A.  B.  C.  D.

11. 若一次函数的图象经过第一、二、四象限，则(    )

A.  B.  C.  D.

12. 若，则(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）

13. 如图，已知，，，则_________．
14. 定义：一个三角形的一边长是另一边长的倍，这样的三角形叫做“倍长三角形”若等腰是“倍长三角形”，底边的长为，则腰的长为______．
15. 一次数学知识竞赛中，竞赛题共题．规定：答对一道题得分，不答或答错一道题倒扣分，甲同学答对道题，答错道题，则甲同学得____分；若得分不低于分者获奖，则获奖者至少应答对____道题．
16. 在画一次函数的图象时，小雯同学列表如下，其中“”表示的数为____

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

17. 本小题分
    如图，点在上，，，，求证：≌．

18. 本小题分

如图，≌，点在边上，与交于点，已知，，，．

求的度数；

求与的周长和．

19. 本小题分

已知：如图，把正三角形的边延长一倍至点，连结求证：是直角三角形．

20. 本小题分
    解不等式：，并把解集在数轴上表示出来．
    
    解不等式组，并写出它的最大整数解．
21. 本小题分

在如图所示的正方形网格中，每个小正方形的边长均为，的三个顶点恰好是正方形网格的格点．

写出图中所示各顶点的坐标；

求出此三角形的面积．

22. 本小题分
    已知，如图，在平面直角坐标系中，，，点在第一象限内，点从原点出发，以每秒个单位长度的速度沿着长方形移动一周即：沿着的路线移动．
    

写出点的坐标：          

当点移动了时，描出此时点的位置，并求出点的坐标

在移动过程中，当点到轴的距离为个单位长度时，求点移动的时间．

23. 本小题分

写出下列各题中与之间的关系式，并判断是否为的一次函数，是否为正比例函数．

动车以千米时的速度匀速行驶，行驶路程千米与行驶时间时之间的关系．

正方形的面积与它的对角线长之间的关系．

一棵树现在高厘米，每个月长高厘米，个月后这棵树的高度为厘米．与之间的关系．

24. 本小题分

某地区居民生活用水的收费标准为：全月用水量若不超过立方米，则水费为每立方米元若超过立方米，则超过部分水费为元立方米设全月用水立方米，应付水费为元．

当时，求关于的函数表达式，并求自变量的取值范围．

某月，小明家用水立方米，小红家用水立方米，这两家该月应缴水费多少元

25. 本小题分

已知与成正比例，且当时，．

写出与之间的函数关系式．

计算当时，的值．

计算当时，的值．

答案和解析

1.【答案】 

【解析】解：在和中，

．
故选：．
 

2.【答案】 

【解析】

【分析】
本题考查作图三角形，解题的关键是理解题意．
观察做法可知：即可得出已知条件是已知两边及夹角，据此判断即可．
【解答】
解：观察做法可知：线段等于已知线段，等于已知角，线段等于已知线段，
即已知两边及夹角．
故选：．  

3.【答案】 

【解析】

【分析】
本题考查的是勾股定理，勾股定理逆定理有关知识，连接，分别在格点三角形中，根据勾股定理即可得到，，的长度，然后利用勾股定理的逆定理求出，继而可得出的度数．
【解答】
解：连接．

，，，
，
，
是直角三角形，，
，
．  

4.【答案】 

【解析】略
 

5.【答案】 

【解析】略
 

6.【答案】 

【解析】

【分析】
本题考查的是解一元一次不等式，熟知解一元一次不等式的基本步骤是解答此题的关键．
先去分母，再去括号，移项，再合并同类项即可．
【解答】
解：去分母得，，
去括号得，，
移项得，，
合并同类项得，．
故选D．  

7.【答案】 

【解析】

【分析】本题主要考查的是坐标确定位置的有关知识，过点作轴于点，然后求出，，从而解出此题．
【解答】

解：如图，过点作轴于，
易得，，
．
故选C．
 

8.【答案】 

【解析】

【分析】
本题考查了点的坐标，到轴的距离，熟记点到轴的距离等于纵坐标的绝对值是解题的关键．根据点到轴的距离等于纵坐标的绝对值解答．
【解答】
解：点，
点到轴的距离为，
故选B．  

9.【答案】 

【解析】是的一次函数，且，随的增大而减小，据此判断即可．
解：是的一次函数，且，随的增大而减小，且；

故选：．
本题考查的是一次函数上点的坐标特征和性质，掌握一次函数的性质是关键．
 

10.【答案】 

【解析】

【分析】
本题考查了正比例函数的定义，解题关键是掌握正比例函数的定义条件：正比例函数的定义条件是：为常数且，自变量次数为．
由正比例函数的定义可得，解之即可．
【解答】
解：由正比例函数的定义可得：，
解得：．
故选B．  

11.【答案】 

【解析】一次函数的图象经过第一、二、四象限，
，，
，
，故A正确．
故选A．
 

12.【答案】 

【解析】解：、，，，但是，不符合题意；
B、，，，但是，不符合题意；
C、，，，，符合题意；
D、，，，但是，不符合题意．
故选：．
举出反例即可判断、、，根据不等式的传递性即可判断．
本题考查了不等式的性质，应用不等式的性质应注意的问题：在不等式的两边都乘以或除以同一个负数时，一定要改变不等号的方向；当不等式的两边要乘或除以含有字母的数时，一定要对字母是否大于进行分类讨论．不等式的传递性：若，，则．
 

13.【答案】 

【解析】

【分析】
本题考查了三角形外角性质，平行线的性质的应用，解此题的关键是求出的度数，注意：两直线平行，同位角相等．延长交于，根据平行线的性质求出，求出，根据三角形外角性质得出，代入求出即可．
【解答】
解：延长交于，

，，
，
，
，
，
故答案为．  

14.【答案】 

【解析】解：等腰是“倍长三角形”，
或，
若，则三边分别是，，，符合题意，
腰的长为；
若，则，三边分别是，，，
，
此时不能构成三角形，这种情况不存在；
综上所述，腰的长是，
故答案为：．
由等腰是“倍长三角形”，可知或，若，可得的长为；若，因，故此时不能构成三角形，这种情况不存在；即可得答案．
本题考查三角形三边关系，涉及新定义，解题的关键是分类思想的应用及掌握三角形任意两边的和大于第三边．
 

15.【答案】； 

【解析】

【分析】
此题考查了一元一次不等式的应用，解决问题的关键是读懂题意，依题意列出不等式进行求解．
先求出答对题所得的分，再减去答错题的分，即可求出甲同学所得的分；用答对题所得的分减去不答或答错题所扣的分数应分，列出不等式进行求解即可．
【解答】
解：根据题意答对道题，答错道题得分为：分．
设获奖者应答对道题，竞赛题共题，故不答或答错的为题，
得分不低于分获奖，
，
解得．
故答案为；．  

16.【答案】 

【解析】解：设该函数的解析式为，
点，在该函数图象上，
，
解得，
即该函数解析式为，
当时，，
故答案为：．
根据表格中的数据，可以先求出该函数的解析式，然后将代入求出相应的的值即可．
本题考查一次函数的图象，解答本题的关键是求出相应的函数解析式．
 

17.【答案】证明：，，，
，
，，
，
在和中，
，
≌． 

【解析】根据一线三垂直模型利用证明≌即可．
本题考查了全等三角形的判定，熟练掌握一线三垂直模型是解题的关键．
 

18.【答案】解：，，
，
≌，
，
，
即的度数为；
≌，
，，
与的周长和． 

【解析】本题考查的是全等三角形的性质、角的和与差的应用，掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键．
根据全等三角形的性质得到，计算即可；
根据全等三角形的性质求出、，根据三角形的周长公式计算即可．
 

19.【答案】由已知，，得，，即是直角三角形． 

【解析】略
 

20.【答案】解：移项，得：，
合并同类项，得：，
系数化为，得：，
将不等式的解集表示在数轴上如下：

解不等式，得：，
解不等式，得：，
则不等式组的解集为，
其最大整数解为． 

【解析】根据解一元一次不等式基本步骤：移项、合并同类项、系数化为可得；
分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集．
本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
 

21.【答案】解：，，；
如图所示：



． 

【解析】本题考查了坐标与图形的性质，熟练掌握平面直角坐标系的坐标的特点是解题的关键．
根据平面直角坐标系的特点写出各点的坐标即可；
根据的面积，即可解答．
 

22.【答案】解：

点以每秒个单位长度的速度

沿着长方形移动，点移动了，
点移动了个单位，即，
则点在上且距点个单位，
 点的坐标为 

分两种情况讨论：第一次距轴个单位时，
即，
点移动的时间  
第二次距轴个单位时，，
即，
点移动的时间为 ，

综上所述，  或  时，点到轴的距离为个单位长度．

【解析】

【分析】
此题主要考查了点的坐标，长方形的性质．正确的求出点的坐标是解决问题的关键．
根据点，坐标，从而得出、长，再根据矩形性质得出点坐标即可；
先求出点移动秒时的距离，从而得出点在边上，从而求的长，即可得出点坐标；
分两种情况：当点在边上时，当点在边上时，分别求解即可．
【解答】
解：，，
，，
长方形，
，
故答案为；
见答案；
见答案．  

23.【答案】解：，是的一次函数，也是的正比例函数．

，不是的正比例函数，也不是的一次函数．

，是的一次函数，不是的正比例函数．

【解析】略
 

24.【答案】．
小明家应缴水费元，小红家应缴水费元． 

【解析】略
 

25.【答案】．
．
． 

【解析】略