2023年中考数学（苏科版）总复习一轮课时训练 24　解直角三角形的应用(含答案)

这是一份2023年中考数学（苏科版）总复习一轮课时训练 24　解直角三角形的应用(含答案)，共6页。
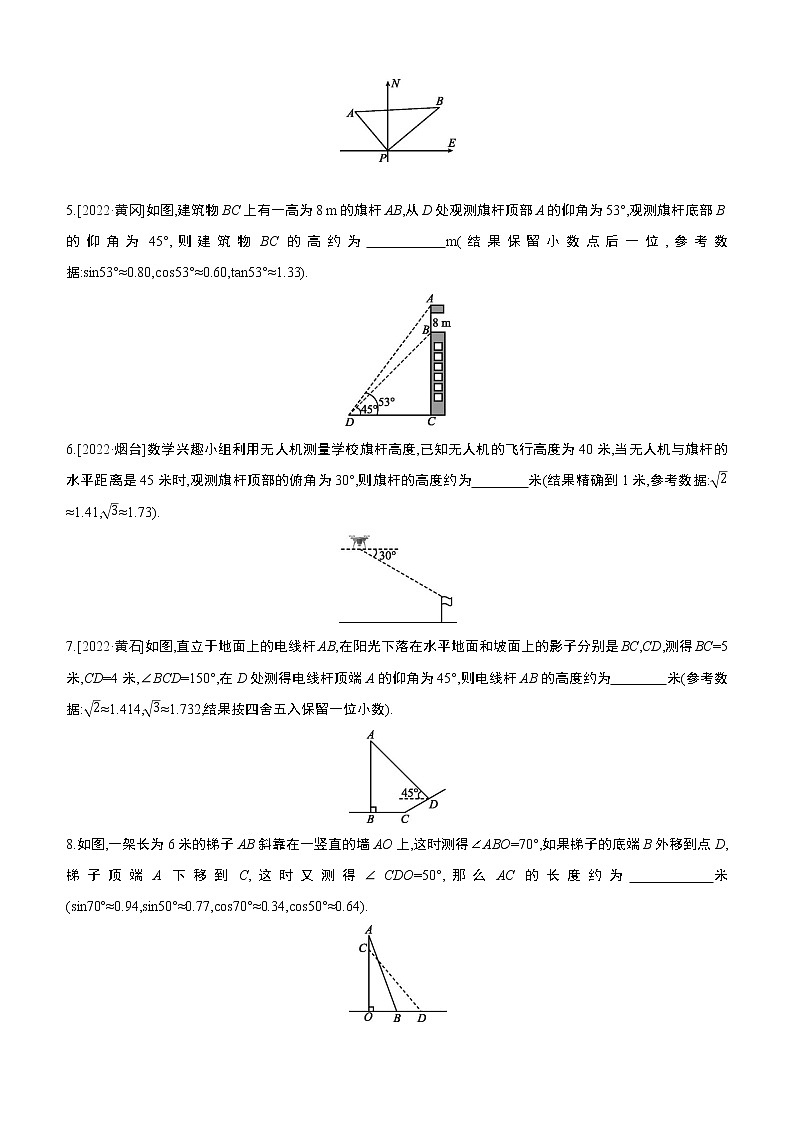
解直角三角形的应用夯实基础1.[2021·温州]如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为              (　　) A.(1.5+150tanα)米  B.1.5+米C.(1.5+150sinα)米  D.1.5+米2.[2021·安徽]如图,在Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为 (　　) A.  B. C.  D.43.如图,一艘船由A港沿北偏东65°方向航行30 km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为              (　　) A.(30+30) km  B.(30+10) kmC.(10+30) km  D.30 km4.[2022·玉林]如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点A,B处,且相距20海里,如果知道甲船沿北偏西40°方向航行,则乙船沿　　　　　　　方向航行.  5.[2022·黄冈]如图,建筑物BC上有一高为8 m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为　　　　m(结果保留小数点后一位,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33). 6.[2022·烟台]数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为　　　　米(结果精确到1米,参考数据:≈1.41,≈1.73). 7.[2022·黄石]如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC,CD,测得BC=5米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为45°,则电线杆AB的高度约为　　　　米(参考数据:≈1.414,≈1.732,结果按四舍五入保留一位小数). 8.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到点D,梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为　　　　米(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64).  9.[2022·自贡]如图,在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度(结果精确到0.1,参考数据tan37°≈0.75,tan53°≈1.33,≈1.73).10.[2022·凉山州]王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,如图,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走2米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1∶3(点E,C,B在同一水平线上).(1)求王刚同学从点C到点D的过程中上升的高度;(2)求大树AB的高度(结果保留根号). 拓展提升11.[2022·盐城]某种落地灯如图①所示,AB为立杆,其高为84 cm;BC为支杆,它可绕点B旋转,其中BC长为54 cm;DE为悬杆,滑动悬杆可调节CD的长度.支杆BC与悬杆DE之间的夹角∠BCD为60°.(1)如图②,当支杆BC与地面垂直,且CD的长为50 cm时,求灯泡悬挂点D距离地面的高度;(2)在图②所示的状态下,将支杆BC绕点B顺时针旋转20°,同时调节CD的长(如图③),此时测得灯泡悬挂点D到地面的距离为90 cm,求CD的长.(结果精确到1 cm,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)　　　　 
答案1.A　2.C3.B　如图,由题中方向角可知∠A=45°,∠ABC=75°,∠C=60°,过点B作BD⊥AC于点D,在Rt△ABD中,∠A=45°,AB=30,∴AD=ABcosA=30,BD=ABsinA=30,在Rt△BCD中,∠C=60°,∴CD==10,∴AC=AD+CD=30+10,故选B.4.北偏东50°(或东偏北40°)　由题意可知,AP=12,BP=16,AB=20,所以AP2+BP2=AB2,∠APB=90°.所以∠NPB=50°.故答案为北偏东50°(或东偏北40°).5.24.2　在Rt△BCD中,∠BDC=45°,则BC=CD,设BC=CD=x,则AC=x+8,在Rt△ACD中,tan∠ADC=,则x+8=x·tan53°,∴x+8≈1.33x,∴x≈24.2(m),故建筑物BC的高约为24.2 m.6.14　如图,过O点作OC⊥AB于C点,∵当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,∴AC=45米,∠CAO=30°,∴OC=AC·tan30°=×45=15(米),∴旗杆的高度=40-15≈14(米).7.10.5　延长AD交BC的延长线于E,作DF⊥BE于F,∵∠BCD=150°,∴∠DCF=30°,又CD=4,∴DF=2,CF=2,由题意得∠E=45°,∴EF=DF=2,∴BE=BC+CF+EF=5+2+2=7+2,∴AB=BE×tanE=(7+2)×1≈10.5(米).8.1.02　∵∠ABO=70°,AB=6米,∴sin70°=≈0.94,解得:AO≈5.64米,∵∠CDO=50°,DC=6米,∴sin50°=≈0.77,解得:CO≈4.62米,则AC=5.64-4.62=1.02(米),故答案为:1.02.9.解:由题意可知AB=24米,∠BDA=53°,∴tan∠BDA=≈1.33,∴AD≈≈18.05.∵tan∠CAD=tan30°=≈,∴CD≈18.05×≈10.4(米).故办公楼的高度约为10.4米.10.解:(1)过点D作DH⊥CE于点H,由题意知CD=2米,∵斜坡CF的坡比为i=1∶3,∴,设DH=x米,则CH=3x米,∵DH2+CH2=DC2,∴x2+(3x)2=(2)2,∴x=2(负值已舍去),∴DH=2米,CH=6米,答:王刚同学从点C到点D的过程中上升的高度为2米.(2)过点D作DG⊥AB于点G,∵∠DHB=∠DGB=∠ABC=90°,∴四边形DHBG为矩形,∴DH=BG=2米,DG=BH=BC+CH,设BC=y米,∴DG=(y+6)米,∵∠ACB=45°,∠ABC=90°,∴BC=AB=y(米),∴AG=(y-2)米,∵∠ADG=30°,∴=tan30°=,∴,∴y=6+4,经检验,y=6+4是方程的解,∴AB=(6+4)米.答:大树AB的高度是(6+4)米.11.解:(1)如图①,过点D作DF⊥BC于F.∵∠FCD=60°,∠CFD=90°,∴FC=CD×cos60°=50×=25(cm),∴FA=AB+BC-CF=84+54-25=113(cm),答:灯泡悬挂点D距离地面的高度为113 cm.(2)如图②,过点C作CG垂直地面于点G,过点B作BN⊥CG于N,过点D作DM⊥CG于M,∵BC=54 cm,∴CN=BC×cos20°≈54×0.94=50.76(cm),∴MN=CN+MG-CG=50.76+90-50.76-84=6(cm),∴CM=CN-MN=44.76(cm),∴CD=≈≈58(cm),答:CD的长约为58 cm.