2023年中考数学（苏科版）总复习一轮课时训练 35　数据的分析(含答案)

这是一份2023年中考数学（苏科版）总复习一轮课时训练 35　数据的分析(含答案)，共6页。试卷主要包含了[2022·永州]已知一列数据，2岁B等内容，欢迎下载使用。
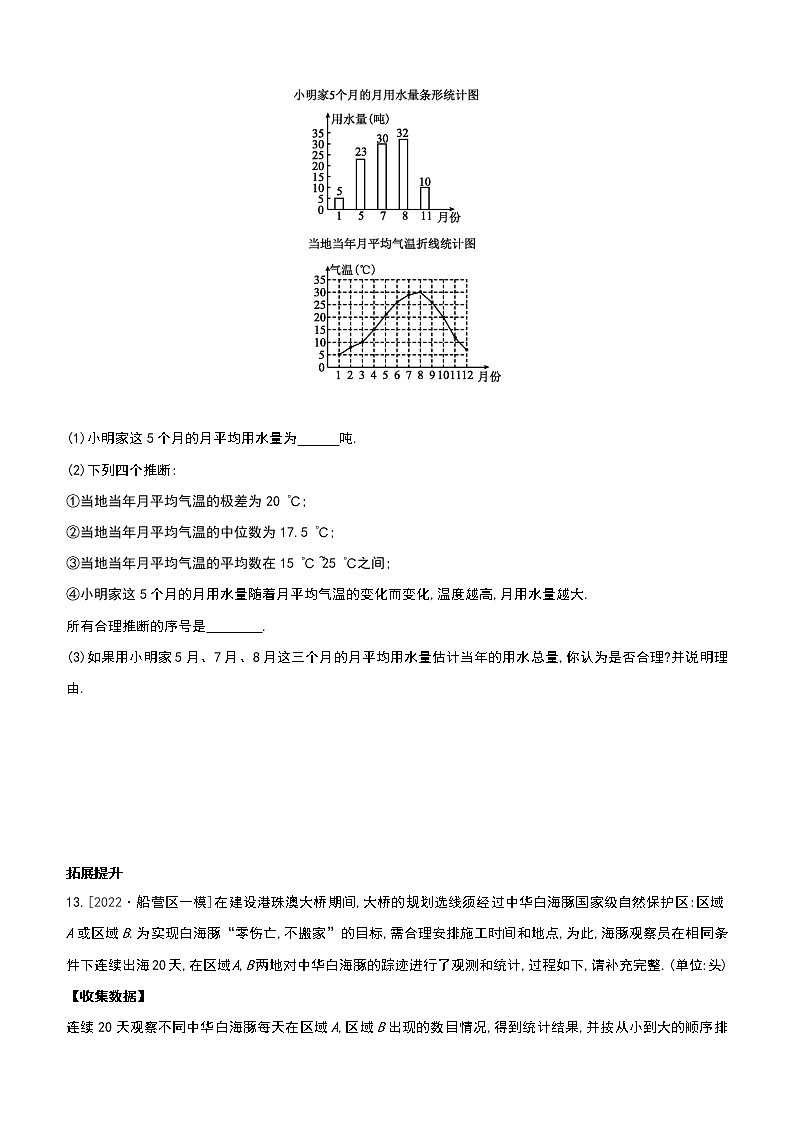
数据的分析夯实基础1.[2022·永州]已知一列数据:27,12,12,5,7,12,5,该列数据的众数是 (　　)A.27 B.12 C.7 D.52.[2022·湘西州]据悉,在2022年湘西州“三独”比赛中,某校11名参赛同学的成绩各不相同,按照成绩,取前5名进入决赛.如果小红知道了自己的比赛成绩,要判断自己能否进入决赛,小红还需知道这11名同学成绩的              (　　)A.平均数  B.中位数C.众数  D.方差3.[2022·大连]某校健美操队共有10名队员,统计队员的年龄情况,结果如下:13岁3人,14岁5人,15岁2人.该健美操队队员的平均年龄为              (　　)A.14.2岁  B.14.1岁C.13.9岁  D.13.7岁4.[2022·嘉兴]5月1日至7日,我市每日最高气温如图所示,则下列说法错误的是 (　　) A.中位数是33 ℃  B.众数是33 ℃C.平均数是 ℃  D.4日至5日最高气温下降幅度较大5.某鞋厂调查了商场一个月内不同尺码男鞋的销量,在平均数、中位数、众数和方差等数个统计量中,该鞋厂最关注的是　　　　. 6.[2022·连云港]一组数据2,1,3,1,2,4的中位数是　　　　. 7.[2022·贵港]甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均数都是8环,方差分别为=1.4,=0.6,则两人射击成绩比较稳定的是　　　　(填“甲”或“乙”). 8.[2021·淮安]已知一组数据1,3,a,10的平均数为5,则a=　　　　. 9.[2021·镇江]在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为　　　　.  10.[2022·永州]某初级中学坚持开展阳光体育活动,七年级至九年级每学期均进行体育技能测试.其中A班甲、乙两位同学6个学期的投篮技能测试成绩(投篮命中个数)折线图如图所示.为参加学校举行的毕业篮球友谊赛,A班需从甲、乙两位同学中选1人进入班球队,从两人成绩的稳定性考虑,请你决策A班应该选择的同学是　　　　. 11.[2022·北部湾经济区]某水果公司以10元/kg的成本价新进2000箱荔枝,每箱质量5 kg,在出售荔枝前,需要去掉损坏的荔枝,现随机抽取20箱,去掉损坏荔枝后称得每箱的质量(单位: kg)如下:4.7　4.8　4.6　4.5　4.8　4.9　4.84.7　4.8　4.7　4.8　4.9　4.7　4.84.5　4.7　4.7　4.9　4.7　5.0整理数据:质量(kg)4.54.64.74.84.95.0数量(箱)217a31分析数据:平均数众数中位数4.75bc(1)直接写出上述表格中a,b,c的值.(2)平均数、众数、中位数都能反映这组数据的集中趋势,请根据以上样本数据分析的结果,任意选择其中一个统计量,估算这2000箱荔枝共损坏了多少千克.(3)根据(2)中的结果,求该公司销售这批荔枝每千克定为多少元才不亏本(结果保留一位小数).  12.[2022·玄武区一模]随机抽取小明家一年中5个月的月用水量(单位:吨),并对当地当年月平均气温(单位: ℃)进行了统计,得到如图所示的统计图. (1)小明家这5个月的月平均用水量为　　　吨. (2)下列四个推断:①当地当年月平均气温的极差为20 ℃;②当地当年月平均气温的中位数为17.5 ℃;③当地当年月平均气温的平均数在15 ℃~25 ℃之间;④小明家这5个月的月用水量随着月平均气温的变化而变化,温度越高,月用水量越大.所有合理推断的序号是　　　　. (3)如果用小明家5月、7月、8月这三个月的月平均用水量估计当年的用水总量,你认为是否合理?并说明理由.     拓展提升13.[2022·船营区一模]在建设港珠澳大桥期间,大桥的规划选线须经过中华白海豚国家级自然保护区:区域A或区域B.为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海20天,在区域A,B两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)【收集数据】连续20天观察不同中华白海豚每天在区域A,区域B出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:区域A0134566678891114151517232530区域B11346689111214151616161722252635【整理、描述数据】(1)按如下数段整理、描述这两组数据,请补充完整:海豚数x0≤x≤78≤x≤1415≤x≤2122≤x≤2829≤x≤35区域A953　　 　　 区域B65531(2)两组数据的极差、平均数、中位数,众数如下表所示:观测点极差平均数中位数众数区域Aa10.65bc区域B3413.151316请填空:上表中,极差a=　　　　,中位数b=　　　　,众数c=　　　　; (3)规划者们选择了区域A为大桥的必经地,为减少施工对白海豚的影响,需合理安排施工时间,估计在接下来的200天施工期内,区域A大约有多少天中华白海豚出现的数目在22≤x≤35的范围内? 
答案1.B　2.B　3.C　4.A5.众数6.27.乙8.6　依题意有(1+3+a+10)÷4=5,解得a=6.9.1　从小到大排列的五个数x,3,6,8,12的中位数是6,∵再加入一个数,这六个数的中位数与原来五个数的中位数相等,∴加入的这个数是6,∵这六个数的平均数与原来五个数的平均数相等,∴(x+3+6+8+12)=(x+3+6+6+8+12),解得x=1.故答案为1.10.甲　根据折线统计图可知,甲的投篮技能测试成绩起伏小,比较平稳,乙的投篮技能测试成绩起伏大,不稳定,因此A班应该选择的同学是甲.11.解:(1)a=6,b=4.7,c=4.75.　 a=20-2-1-7-3-1=6.分析数据:样本中,4.7出现的次数最多,故众数b为4.7,将数据从小到大排列,中间的两个数为4.7,4.8,故中位数c==4.75,∴a=6,b=4.7,c=4.75.(2)答案不唯一,如选择众数4.7,这2000箱荔枝共损坏了2000×(5-4.7)=600(千克).(3)10×2000×5÷(2000×5-600)≈10.7(元),答:该公司销售这批荔枝每千克定为10.7元才不亏本.12.解:(1)20　(5+23+30+32+10)÷5=20(吨),故答案为20.(2)②③④　月平均最高气温是30 ℃,月平均最低气温是5 ℃,月平均气温的极差为30-5=25(℃),因此①不正确;将12个月的月平均气温从小到大排列后处在中间位置的两个数的平均数为=17.5,因此中位数是17.5 ℃,所以②正确;通过取近似值计算平均数可得,(5+8+10+15+20+25+28+30+26+20+12+7)÷12≈17.2 ℃,因此③正确;从两个统计图中数量的变化情况可知,小明家这5个月的月用水量随着月平均气温的变化而变化,温度越高,月用水量越大,因此④正确.故答案为:②③④.(3)不合理,选取的5,7,8这三个月的当地月平均气温都比较高,这三个月的月用水量都比较多,这样选取的样本缺乏代表性.13.解:(1)2　1　(2)30　8　6(3)200×=30(天).答:区域A大约有30天中华白海豚出现的数目在22≤x≤35的范围内.