2022-2023学年冀教版九年级上册数学期末复习试卷+

这是一份2022-2023学年冀教版九年级上册数学期末复习试卷+，共17页。试卷主要包含了方程，二次函数y＝5x等内容，欢迎下载使用。

2022-2023学年冀教新版九年级上册数学期末复习试卷
一．选择题（共12小题，满分36分，每小题3分）
1．从一副扑克牌中抽出5张红桃、4张梅花、3张黑桃放在一起洗匀后，从中一次随机抽出8张，其中红桃这种花色（　　）
A．不可能抽到 B．可能抽到
C．很有可能抽到 D．一定能抽到
2．方程（x﹣1）（x+3）＝12化为ax2+bx+c＝0的形式后，a、b、c的值为（　　）
A．1、2、﹣15 B．1、﹣2、﹣15 C．﹣1、﹣2、﹣15 D．﹣1、2、﹣15
3．已知Rt△ABC中，∠C＝90°，AC＝2，BC＝3，那么下列各式中正确的是（　　）
A．sinA＝ B．tanA＝ C．tanB＝ D．cosB＝
4．二次函数y＝5x（x﹣1）的一次项系数是（　　）
A．1 B．﹣1 C．2 D．﹣5
5．公园里有两个相似三角形地块，相似比为2：3，面积差是30平方米，那么面积和为（　　）平方米．
A．58 B．68 C．78 D．150
6．将圆柱的侧面展开，能得到的平面图形是（　　）
A．圆形 B．三角形 C．梯形 D．长方形
7．下列条件中，不能判断△ABC和△A1B1C1相似的是（　　）
A．∠C＝∠C1＝90°，∠B＝∠A1＝50°
B．AB＝AC，A1B1＝A1C1，∠B＝∠B1
C．，∠A＝∠A1
D．∠A＝∠A1＝90°，
8．如图，在Rt△ABC中，∠B＝90°，∠A＝60°，AB＝2cm，以B为圆心，以1.5cm长为半径作圆，则⊙B与AC的位置关系是（　　）

A．相离 B．相切 C．相交 D．外切
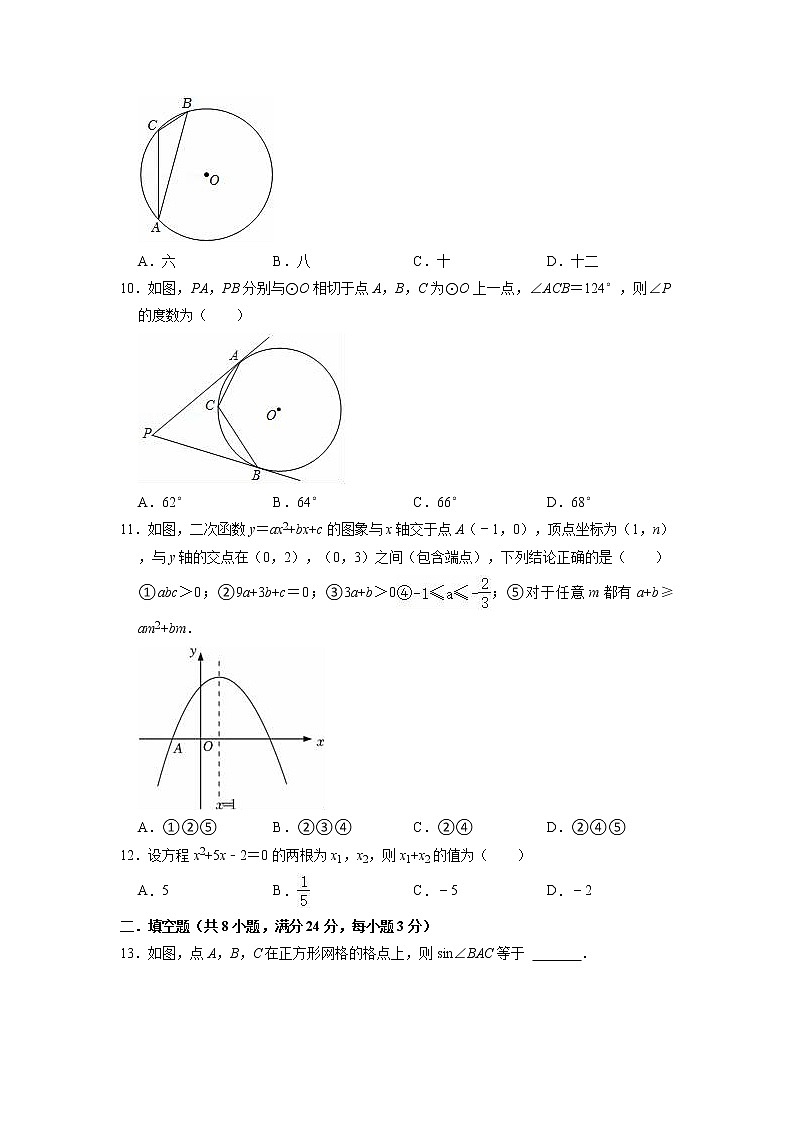
9．如图，AB，AC分别为⊙O的内接正三角形、正四边形的一边，BC是圆内接正n边形的一边，则n为（　　）

A．六 B．八 C．十 D．十二
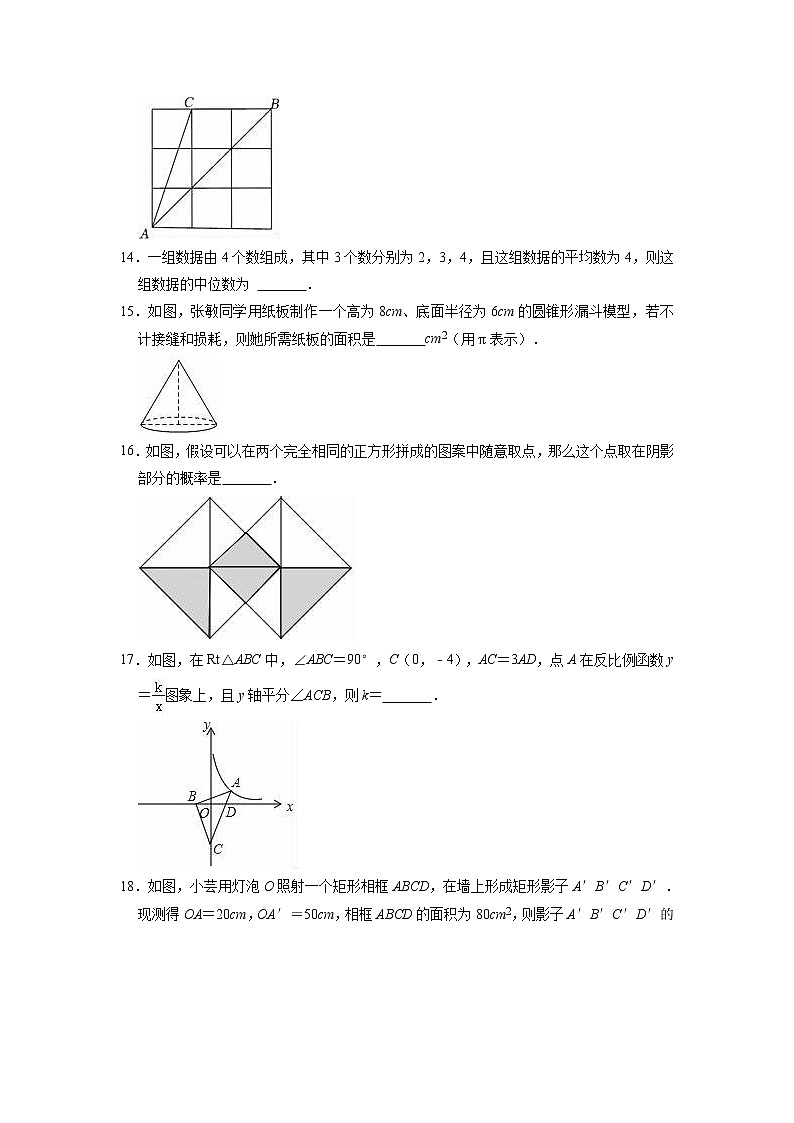
10．如图，PA，PB分别与⊙O相切于点A，B，C为⊙O上一点，∠ACB＝124°，则∠P的度数为（　　）

A．62° B．64° C．66° D．68°
11．如图，二次函数y＝ax2+bx+c的图象与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2），（0，3）之间（包含端点），下列结论正确的是（　　）
①abc＞0；②9a+3b+c＝0；③3a+b＞0；⑤对于任意m都有a+b≥am2+bm．

A．①②⑤ B．②③④ C．②④ D．②④⑤
12．设方程x2+5x﹣2＝0的两根为x1，x2，则x1+x2的值为（　　）
A．5 B． C．﹣5 D．﹣2
二．填空题（共8小题，满分24分，每小题3分）
13．如图，点A，B，C在正方形网格的格点上，则sin∠BAC等于 　 　．

14．一组数据由4个数组成，其中3个数分别为2，3，4，且这组数据的平均数为4，则这组数据的中位数为 　 　．
15．如图，张敏同学用纸板制作一个高为8cm、底面半径为6cm的圆锥形漏斗模型，若不计接缝和损耗，则她所需纸板的面积是　 　cm2（用π表示）．

16．如图，假设可以在两个完全相同的正方形拼成的图案中随意取点，那么这个点取在阴影部分的概率是　 　．

17．如图，在Rt△ABC中，∠ABC＝90°，C（0，﹣4），AC＝3AD，点A在反比例函数y＝图象上，且y轴平分∠ACB，则k＝　 　．

18．如图，小芸用灯泡O照射一个矩形相框ABCD，在墙上形成矩形影子A′B′C′D′．现测得OA＝20cm，OA′＝50cm，相框ABCD的面积为80cm2，则影子A′B′C′D′的面积为　 　cm2．
19．如图，在菱形ABCD中，AC是对角线，AB＝AC＝2，⊙A与边BC相切，则图中阴影部分的面积为是 　 　．

20．如图所示，为了测量出某学校教学大楼AB的高度，数学课外小组同学在C处，测得教学大楼顶端A处的仰角为45°；随后沿直线BC向前走了15米后到达D处，在D处测得A处的仰角为30°，已知测量器高1米，则建筑物AB的高度约为 　 　米．（参考数据：≈1.414，≈1.732，结果按四舍五入保留整数）

三．解答题（共5小题，满分60分）
21．在一个不透明的盒子中，装着分别标着1～3号的三个白球，和分别标着1～2号的两个黄球，它们除颜色、号码不同外，其余均相同．若从中随机摸出两个球．
（1）请用树形图或其它适当的形式把所有可能产生的结果全部列举出来；
（2）求摸出的两个球恰好都是白球的概率．
22．2020年初的新冠肺炎疫情对大们的生活造成了较大的影响，为响应教育部下发通知“停课不停学”的倡议，某校准备选用合适的软件对全校学生直播上课，经对直接软件功能进行筛选，学校选定了“钉钉”和“QQ直播”两款软件进行试用，并组全校师生对这两款软件打分（均为整数，最高5分：最低1分），随机抽取20名同学和10位教师的打分情况作为样本，分析过程如下．
A．收集数据：20名同学打分情况如下：
钉钉
5
4
5
1
4
2
5
3
4
1
1
3
5
4
2
4
4
3
2
5
QQ直播
4
3
3
3
5
5
3
4
5
2
2
5
4
4
4
1
3
2
3
2
B．整理、描述数据：根据学生的打分情况，绘制了如下尚不完整的条形统计图：

C．分析数据：学生打分的平均数、众数、中位数如下表：
软件
平均数
众数
中位数
钉钉
3.35
4
A
QQ直播
3.35
B
3
D．抽取的10位教师对“钉钉”和“QQ直播”这两款软件打分的平均分分别为4.4分和4分．
请根据以上信息解答下列问题：
（1）请补全条形统计图；
（2）填空：a＝　 　，b＝　 　；
（3）你认为学生对这两款软件评价较高的是 　 　，（填“钉钉”或“QQ直播”）理由是 　 　；
（4）学校决定选择综合平均分高的软件进行教学，其中综合平均分中教师打分占60%，学生打分占40%，请你通过计算分析学校会采用哪款软件进行教学．
23．如图，在△ABC中，AB＝AC，以AB为直径的⊙O与边BC，AC分别交于D，E两点，点D作DH⊥AC于点H．
（1）判断DH与⊙O的位置关系，并说明理由；
（2）当cosC＝，BC＝10时，求的值．

24．已知点P（x1，y1）、Q（x2，y2）在反比例函数y＝﹣的图象上，且x1＜x2．试比较y1与y2的大小．
25．如图，抛物线y＝﹣x2+bx+c与x轴交于点A（2，0），交y轴于点B（0，），直线y＝kx﹣过点A与y轴交于点C，与抛物线的另一个交点是D．
（1）求抛物线的解析式；
（2）设点P是直线AD上方的抛物线上一动点（不与点A、D重合），过点P作y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．


参考答案与试题解析
一．选择题（共12小题，满分36分，每小题3分）
1．解：从一副扑克牌中抽出5张红桃、4张梅花、3张黑桃放在一起洗匀后，从中一次随机抽出8张，
若抽出全部4张梅花、3张黑桃，则还会抽出1张红桃，
所以其中红桃这种花色一定能抽到，
故选：D．
2．解：∵原方程化成成一元二次方程的一般形式为x2+2x﹣15＝0，
∴a＝1，b＝2，c＝﹣15．
故选：A．
3．解：Rt△ABC中，∠C＝90°，
∵AC＝2，BC＝3，
∴AB＝＝，
∴sinA＝＝，tanA＝＝，tanB＝＝，cosB＝＝，
故选：C．
4．解：∵原二次函数可化为y＝5x2﹣5x，
∴其一次项系数是﹣5．
故选：D．
5．解：∵两相似三角形的相似比为2：3，
∴它们的面积比为4：9，
设较小三角形的面积为4x，则较大三角形的面积为9x，
则有：9x﹣4x＝30，
解得：x＝6，
∴9x+4x＝13x＝78．
故选：C．
6．解：将圆柱的侧面沿着母线剪开展平，可以得到长方形，
故选：D．
7．A．根据两角对应相等的两个三角形相似，可得△ABC和△A1B1C1相似；故本选项不符合题意；
B．∵AB＝AC，A1B1＝A1C1，
∴∠B＝∠C，∠B1＝∠C1，
∵∠B＝∠B1，
∴∠C＝∠C1，
∴△ABC∽△A1B1C1，
故本选项不符合题意；
C．对应边成比例，夹角不一定相等，不能判定△ABC和△A1B1C1相似．故本选项符合题意；
D．∵∠A＝∠A1＝90°，，
∴△ABC∽△A1B1C1，
故本选项不符合题意；
故选：C．
8．解：过点B作BE⊥AC于点E，

在Rt△ABE中，∠A＝60°，
∴sinA＝，
∴BE＝cm，
∵＞1.5，
∴⊙B与AC相离，
故选：A．
9．解：连接OA、OB、OC，如图，

∵AC，AB分别为⊙O的内接正四边形与内接正三角形的一边，
∴∠AOC＝＝90°，∠AOB＝＝120°，
∴∠BOC＝∠AOB﹣∠AOC＝30°，
∴n＝＝12，
即BC恰好是同圆内接一个正十二边形的一边．
故选：D．
10．解：在优弧AB取一点D，连接AD、BD、OA、OB，如图，

∵∠ACB+∠ADB＝180°，
∴∠ADB＝180°﹣124°＝56°，
∴∠AOB＝2∠ADB＝112°，
∵PA、PB分别与⊙O相切于A、B，
∴OA⊥PA，OB⊥PB，
∴∠OAP＝∠OBP＝90°，
∴∠P＝180°﹣∠AOB＝180°﹣112°＝68°．
故选：D．
11．解：由函数图象可a＜0，b＞0，c＞0，
∴abc＜0，故①错误；
∵抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），对称轴直线是x＝1，
∴该抛物线与x轴的另一个交点的坐标是（3，0），
∴当x＝3时，y＝0，
即9a+3b+c＝0，故②正确；
根据图示知，抛物线开口方向向下，则a＜0．
∵对称轴x＝﹣＝1，
∴b＝﹣2a，
∴3a+b＝3a﹣2a＝a＜0，即3a+b＜0，故③错误；
∵抛物线与x轴的两个交点坐标分别是（﹣1，0），（3，0），
∴﹣1×3＝﹣3，
＝﹣3，则a＝﹣．
∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），
∴2≤c≤3，
∴﹣1≤﹣≤﹣，即﹣1≤a≤﹣，故④正确；
∵抛物线的顶点坐标（1，n），
∴x＝1时，二次函数值有最大值n，
∴a+b+c≥am2+bm+c．
即a+b≥am2+bm，所以⑤正确．
故选：D．
12．解：方程x2+5x﹣2＝0的两根为x1，x2，
∴x1+x2＝﹣5，
故选：C．
二．填空题（共8小题，满分24分，每小题3分）
13．解：连接格点CD．
由题图可得：CD＝＝，
AC＝＝，
AD＝＝2．
∵CD2+AD2＝2+8＝10，
AC2＝10，
∴CD2+AD2＝AC2．
∴△ACD是直角三角形，且∠ADC＝90°．
∴sin∠BAC＝
＝
＝．
故答案为：．

14．解：根据题意知，另外一个数为4×4﹣（2+3+4）＝7，
所以这组数据为2，3，4，7，
则这组数据的中位数＝3.5，
故答案为：3.5．
15．解：∵圆锥的母线长＝＝10cm，
l＝2×6×π＝12πcm，
∴S＝lR＝×12π×10＝60πcm2．
故答案为：60π．
16．解：设小正方形边长为a，则阴影部分面积为3a2，
图案总面积8a2﹣a2＝7a2，
因此这个点取在阴影部分的概率是＝．
故答案为．
17．解：作AE⊥y轴于E，如图，
∵C（0，﹣4），
∴OC＝4，
∵OD∥AE，
∴＝＝，
而AC＝3AD，即CD：CA＝2：3，
∴＝＝，
∴OD＝AE，CE＝6，
∴OE＝2，
设A（t，2），则OD＝t，
∵OC平分∠ACB，OC⊥BD，
∴△CBD为等腰三角形，
∴OB＝OD＝t，
∴B（﹣t，0），
∵∠ABC＝90°，
∴AB2+BC2＝AC2，
∴（t+t）2+22+（t）2+42＝t2+62，解得t＝，
∴A（，2），
把A（，2）代入y＝得k＝×2＝．
故答案为．

18．解：∵OA：OA′＝2：5，
可知OB：OB′＝2：5，
∵∠AOB＝∠A′OB′，
∴△AOB∽△A′OB′，
∴AB：A′B′＝2：5，
∴矩形ABCD的面积：矩形A′B′C′D′的面积为4：25，
又矩形ABCD的面积为80cm2，则矩形A′B′C′D′的面积为500cm2．
故答案为：500cm2．
19．解：设以点A为圆心的圆与边BC相切于点F，如图所示，

则AF⊥BC，
∵四边形ABCD是菱形，
∴AB＝BC，
∵AB＝AC＝2，
∴AB＝BC＝AC＝2，
∴△ABC是等边三角形，
∴∠B＝60°，
∴AF＝AB•sin60°＝2×＝，
∴阴影部分的面积＝2×（△ABC的面积﹣扇形AEG的面积）＝2×（×2×﹣）＝2﹣π．
故答案为：2﹣π．
20．解：设AH＝x米，
在Rt△AEH中，
∵∠AEH＝45°，
∴∠EAH＝90°﹣45°，
∴∠AEH＝∠EAH，
∴EH＝AH＝x，
∴FH＝EH+EF＝x+15，
在Rt△AFH中，∠AFH＝30°，tan∠AFH＝，
tan∠30°＝＝，即＝，
解得：x＝≈20.49，
∴AB＝AH+BH＝20.49+1≈21（米），
答：建筑物AB的高度约为21米．
故答案为：21．

三．解答题（共5小题，满分60分）
21．解：（1）树形图如下：

或列表如下：

白1
白2
白3
黄1
黄2
白1

（白2，白1）
（白3，白1）
（黄1，白1）
（黄2，白1）
白2
（白1，白2）

（白3，白2）
（黄1，白2）
（黄2，白2）
白3
（白1，白3）
（白2，白3）

（黄1，白3）
（黄2，白3）
黄1
（白1，黄1）
（白2，黄1）
（白3，黄1）

（黄2，黄1）
黄2
（白1，黄2）
（白2，黄2）
（白3，黄2）
（黄1，黄2）

即所有可能的结果共20种．

（2）从（1）可知，摸到的两个球恰好都是白球的可能结果有
（白1，白2）、（白1，白3）、（白2，白1）、
（白2，白3）、（白3，白1）、（白3，白2）共6种，
所以摸到的两个球都是白球概率是．
22．解：（1）如图，补全的条形统计图如下：


（2）a＝＝4，b＝3．
故答案为：4，3；
（3）学生对这两款软件评价较高的是“钉钉”，
理由是：“钉钉”的众数、中位数都比“QQ直播”的众数、中位数大
故答案为：“钉钉”，“钉钉”的众数、中位数都比“QQ直播”的众数、中位数大；
（4）根据题意，得
4.4×60%+3.35×40%＝3.98（分），
4×60%+3.35×40%＝3.74（分），
∵3.98＞3.74，
∴学校会采用“钉钉”软件进行教学．
23．解：（1）DH与⊙O相切，理由如下：
连接OD．
∵OB＝OD，
∴∠OBD＝∠ODB，
∵AB＝AC，
∴∠ABD＝∠C，
∴∠ODB＝∠C，
∴OD∥AC，
又∵DH⊥AC，
∴∠DHC＝90°，
∴∠ODH＝∠DHC＝90°，
∴OD⊥DH，
又∵OD是⊙O的半径，
∴DH与⊙O相切；

（2）连接BE，AD，
∵AB是⊙O的直径，
∴∠AEB＝90°，
∴∠BEC＝180°﹣∠AEB＝90°，
在Rt△BEC中，cos∠C＝＝，
又∵BC＝10，
∴CE＝2，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∴AD⊥BC，
又∵AB＝AC，
∴DC＝BC＝5（三线合一），
在Rt△ADC中，
∵cos∠C＝＝，
∴AC＝5，
∴AB＝5，
∴AE＝AC﹣CE＝3，
∴＝＝．

24．解：反比例函数y＝﹣的图象在二、四象限，
∵x1＜x2．
∴点P（x1，y1）在点Q（x2，y2）的左侧，
①当点P、Q在第二象限图象上时，即x1＜x2＜0，
∵在第二象限内，y随x的增大而增大，
∴y1＜y2，
②当点P在第二象限、点Q在第四象限的图象上时，即x1＜0＜x2，
由图象可得，y1＞y2，
③当点P、Q在第四象限图象上时，即0＜x1＜x2，
∵在第四象限内，y随x的增大而增大，
∴y1＜y2，
25．解：（1）∵y＝﹣x2+bx+c经过点A（2，0）和B（0，），
∴由此得，
解得
∴抛物线的解析式是y＝﹣x2﹣x+．

（2）设P的坐标是（x，﹣ x2﹣x+），则M的坐标是（x， x﹣）
∴PM＝（﹣x2﹣x+）﹣（x﹣）＝﹣x2﹣x+4，
解方程得：，，
∵点D在第三象限，则点D的坐标是（﹣8，﹣7），由y＝x﹣得点C的坐标是（0，﹣），
∴CE＝﹣﹣（﹣7）＝6，
由于PM∥y轴，要使四边形PMEC是平行四边形，必有PM＝CE，即﹣x2﹣x+4＝6，
解这个方程得：x1＝﹣2，x2＝﹣4，
符合﹣8＜x＜2，
当x＝﹣2时，y＝﹣×（﹣2）2﹣×（﹣2）+＝3，
当x＝﹣4时，y＝﹣×（﹣4）2﹣×（﹣4）+＝，
因此，直线AD上方的抛物线上存在这样的点P，使四边形PMEC是平行四边形，点P的坐标是（﹣2，3）和（﹣4，）．