2022-2023学年华东师大版九年级上册数学期末复习试卷+

2022-2023学年华东师大新版九年级上册数学期末复习试卷

一．选择题（共10小题，满分30分，每小题3分）

1．二次根式在实数范围内有意义，则x可以取的值是（　　）

A．﹣2 B．﹣1 C．0 D．3

2．在七年（1）与七年（2）班举行拔河比赛前，根据双方的实力，环环预测：“七年（1）获胜的机会是80%”，那么下面四个说法正确的是（　　）

A．七年（2）班肯定会输掉这场比赛 

B．七年（1）班肯定会赢得这场比赛 

C．若比赛10次，则七年（1）班会赢得8次 

D．七年（2）班也有可能会赢得这场比赛

3．抛物线y＝x2+2x﹣4的对称轴是（　　）

A．直线x＝2 B．直线x＝﹣2 C．直线x＝1 D．直线x＝﹣1

4．如图，在△ABC中，点D为边AB上的点，下列条件中不能判定△ABC∽△ACD的是（　　）

A．＝ B．＝ C．∠B＝∠ACD D．∠ADC＝∠ACB

5．已知A（2，y1），B（3，y2），C（0，y3）在二次函数y＝ax2+c（a＞0）的图象上，则y1，y2，y3的大小关系正确的是（　　）

A．y3＜y2＜y1 B．y1＜y2＜y3 C．y2＜y1＜y3 D．y3＜y1＜y2

6．在下列说法中，正确的有（　　）

①若x2＝9，则x是9的平方根；

②x＝不是方程x2＝3的根；

③x2﹣12＝0的根是x＝±2；

④x2﹣4x+4＝（x﹣2）2．

A．1个 B．2个 C．3个 D．4个

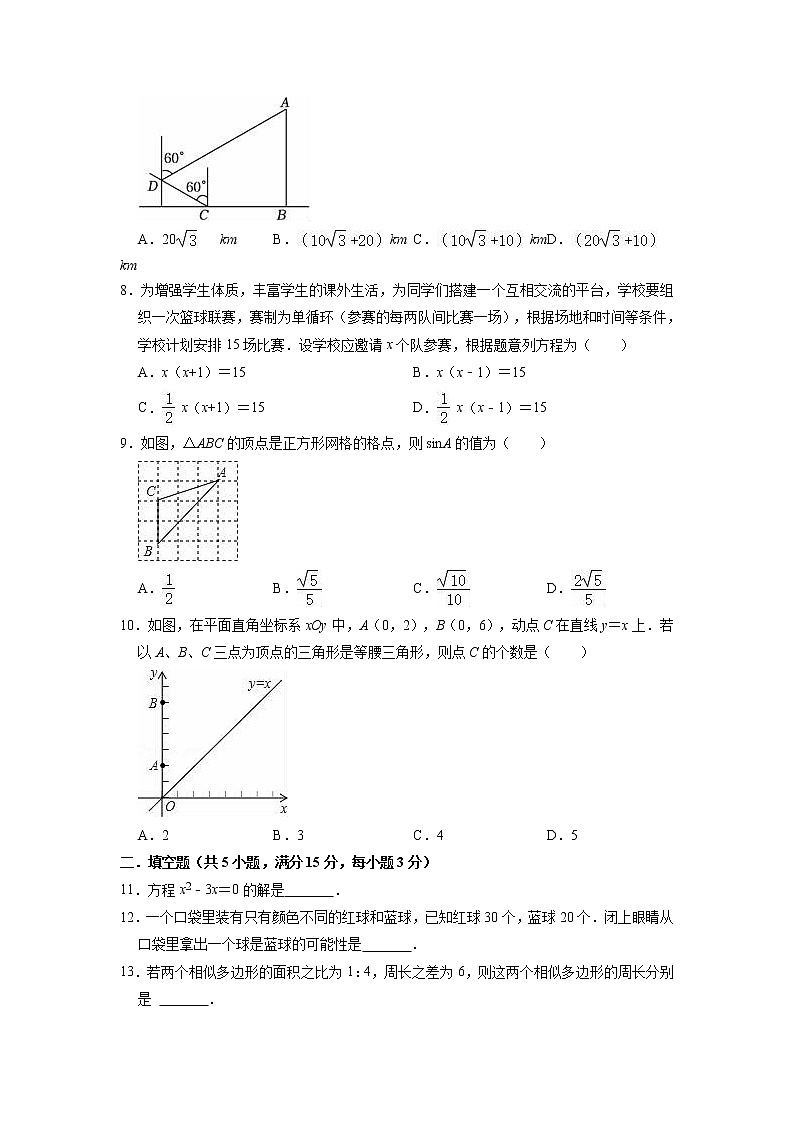
7．一艘货轮从小岛A正南方向的点B处向西航行30km到达点C处，然后沿北偏西60°方向航行20km到达点D处，此时观测到小岛A在北偏东60°方向，则小岛A与出发点B之间的距离为（　　）

A．20km B． km C． km D． km

8．为增强学生体质，丰富学生的课外生活，为同学们搭建一个互相交流的平台，学校要组织一次篮球联赛，赛制为单循环（参赛的每两队间比赛一场），根据场地和时间等条件，学校计划安排15场比赛．设学校应邀请x个队参赛，根据题意列方程为（　　）

A．x（x+1）＝15 B．x（x﹣1）＝15 

C． x（x+1）＝15 D． x（x﹣1）＝15

9．如图，△ABC的顶点是正方形网格的格点，则sinA的值为（　　）

A． B． C． D．

10．如图，在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y＝x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是（　　）

A．2 B．3 C．4 D．5

二．填空题（共5小题，满分15分，每小题3分）

11．方程x2﹣3x＝0的解是　   　．

12．一个口袋里装有只有颜色不同的红球和蓝球，已知红球30个，蓝球20个．闭上眼睛从口袋里拿出一个球是蓝球的可能性是　   　．

13．若两个相似多边形的面积之比为1：4，周长之差为6，则这两个相似多边形的周长分别是 　   　．

14．已知抛物线y＝ax2+bx+c（x为任意实数）经过下图中两点M（1，﹣2）、N（m，0），其中M为抛物线的顶点，N为定点．下列结论：

①若方程ax2+bx+c＝0的两根为x1，x2（x1＜x2），则﹣1＜x1＜0，2＜x2＜3；

②当x＜m时，函数值y随自变量x的减小而减小．

③a＞0，b＜0，c＞0．

④垂直于y轴的直线与抛物线交于C、D两点，其C、D两点的横坐标分别为s、t，则s+t＝2．

其中正确的是　   　（写序号即可）．

15．如图，把菱形ABCD沿着BD的方向平移到菱形A′B′C′D′的位置，若重叠部分的四边形B′EDF的面积是菱形ABCD面积的一半，且BD＝，则此菱形移动的距离是　   　．

三．解答题（共8小题，满分75分）

16．（8分）（1）用适当的方法解方程x2﹣4x+2＝0；

（2）解二元一次方程组；

（3）计算+×﹣sin60°．

17．（9分）介休市位于山西省腹地，太原盆地偏南，历史文化悠久，文明史逾2800年，是人们周末自驾旅游的好去处，“在我可爱的家乡”主题班会中，主持人准备了“绵山风景名胜区”、“张壁古堡”“汾河湿地森林公园”和“秦柏旅游生态园区”这四处风景点的照片各一张，并将它们背面朝上放置（照片背面完全相同），甲同学从中随机抽取一张不放回，乙再从剩下的照片中随机抽取一张，然后甲、乙要根据抽取的照片做相关景点介绍．

（1）甲抽到“绵山风景名胜区”的概率是 　   　；

（2）甲、乙两人中恰好有一人介绍“张壁古堡”的概率．（请用照片序号列表或画树状图）

18．（9分）设一元二次方程x2﹣6x+k＝0的两根分别为x1，x2．

（1）若方程有两个相等的实数根，求k的值；

（2）若k＝5，且x1，x2分别是Rt△ABC的两条直角边的长，试求Rt△ABC的面积．

19．（9分）如图，一海轮位于灯塔P的南偏东60°方向，距离灯塔60海里的A处，它沿正西方向航行一段时间后，到达位于灯塔P的西南方向的B处．

（1）求海轮位于点B处时与灯塔P之间的距离（结果保留根号）；

（2）求航程AB的值（结果保留根号）．

20．（9分）如图1，在△ABC中，∠ACB＝90°，直线l过点C，分别过A、B两点作AE⊥l，BD⊥l，垂足分别为E、D.

（1）求证：△BDC∽△CEA．

（2）如图2，在▱ABCD中，在BC上取点E，使得∠AED＝90°，若AE＝AB，BE＝4，EC＝3，求▱ABCD的面积．

21．（10分）小晨家在毛竹产量很高的山区，现打算建立一个以毛竹为原材料，生产工艺品和座椅的加工厂．第一批生产工艺品和座椅各50件，售后统计，工艺品平均每件利润是160元，座椅平均每件利润是19元，调研发现：

①工艺品每增加1件，工艺品的平均每件利润减少2元；每减少1件，工艺品的平均每件利润增加2元．

②座椅的平均每件利润始终不变．

小晨计划第二批生产工艺品和座椅共100件，设生产的工艺品比第一批增加x件，第二批生产的工艺品和座椅售完后的利润分别为W1，W2（单位：元）．

（1）用含x的代数式分别表示W1，W2；

（2）当x取何值时，第二批生产的工艺品和座椅售完后获得的总利润W最大，最大总利润是多少？

22．（10分）如图，在平面直角坐标系中有M（1，2），N（3，3）两点，如果抛物线y＝ax2（a＞0）与线段MN没有公共点，求a的取值范围．

23．（11分）梅涅劳斯定理：

梅涅劳斯（Menelaus）是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：如图（1），如果一条直线与△ABC的三边AB，BC，CA或它们的延长线交于F、D、E三点，那么一定有••＝1．

下面是利用相似三角形的有关知识证明该定理的部分过程：

证明：如图（2），过点A作AG∥BC，交DF的延长线于点G，则有＝．

任务：（1）请你将上述材料中的剩余的证明过程补充完整；

（2）如图（3），在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，点F在AB上，且BF＝2AF，CF与AD交于点E，则AE＝　   　．

参考答案与试题解析

一．选择题（共10小题，满分30分，每小题3分）

1．解：∵二次根式在实数范围内有意义，

∴x﹣1≥0，

解得：x≥1．

观察选项，只有选项D符合题意．

故选：D．

2．解：80%的机会获胜是发生机会的大小，80%的机会并不是说明比赛胜的场数一定是80%．

七年（1）获胜的机会是80%，即七年（2）班也有可能会赢得这场比赛，只不过获胜的可能性小，只有D选项符合题意．

故选：D．

3．解：∵抛物线y＝x2+2x﹣4＝（x+1）2﹣5，

故对称轴是直线x＝﹣1，

故选：D．

4．解：A、根据两边成比例夹角相等，两三角形相似，可以判定两个三角形相似，本选项不符合题意；

B、两边成比例，不是夹角相等，不能判定三角形相似，本选项符合题意；

C、根据两角对应相等的两个三角形相似，可以判定两个三角形相似，本选项不符合题意；

D、根据两角对应相等的两个三角形相似，可以判定两个三角形相似，本选项不符合题意；

故选：B．

5．解：∵二次函数y＝ax2+c（a＞0），

∴二次函数的开口向上，对称轴是y轴，

∴在对称轴的右侧y随x的增大而增大，

∵0＜2＜3，

∴y3＜y1＜y2，

故选：D．

6．解：若x2＝9，则x是9的平方根，所以①正确；x＝是方程x2＝3的根，所以②错误；x2﹣12＝0的根是x＝±2，所以③正确；x2﹣4x+4＝（x﹣2）2，所以④正确．

故选：C．

7．解：过点D作DE⊥AB于点E，过点C作CF⊥DE于点F，如图所示：

∵∠ABC＝90°，

∴四边形BCFE是矩形，

∴EF＝BC＝30km，CF＝BE，

由题意得：∠DCF＝60°，∠ADE＝90°﹣60°＝30°，

∴∠CDF＝90°﹣60°＝30°，

∴CF＝CD＝×20＝10（km），

∴BE＝10km，

DF＝sin60°×CD＝×20＝10（km），

∴DE＝DF+EF＝（10+30）（km），

∴AE＝tan∠ADE•DE＝tan30°×DE＝×（10+30）＝（10+10）（km），

∴AB＝AE+BE＝10+10+10＝（10+20）（km），

故选：B．

8．解：依题意得： x（x﹣1）＝15．

故选：D．

9．解：如图所示：连接DC，

由网格可得出∠CDA＝90°，

则DC＝，AC＝，

故sinA＝＝＝．

故选：B．

10．解：如图，AB的垂直平分线与直线y＝x相交于点C1，

∵A（0，2），B（0，6），

∴AB＝6﹣2＝4，

以点A为圆心，以AB的长为半径画弧，与直线y＝x的交点为C2，C3，

∵OB＝6，

∴点B到直线y＝x的距离为6×＝3，

∵3＞4，

∴以点B为圆心，以AB的长为半径画弧，与直线y＝x没有交点，

所以，点C的个数是1+2＝3．

故选：B．

二．填空题（共5小题，满分15分，每小题3分）

11．解：原式为x2﹣3x＝0，x（x﹣3）＝0，x＝0或x﹣3＝0，x1＝0，x2＝3．

∴方程x2﹣3x＝0的解是x1＝0，x2＝3．

12．解：闭上眼睛从口袋里拿出一个球是蓝球的可能性是．

13．解：∵两个相似多边形的面积之比为1：4，

∴两个相似多边形的周长之比为1：2，

设两个多边形的周长分别为x，x+6，

则有x+6＝2x，

∴x＝6，

∴这两个相似多边形的周长分别是6，12，

故答案为：6，12．

14．解：①若方程ax2+bx+c＝0的两根为x1，x2（x1＜x2），则﹣1＜x1＜0，2＜x2＜3，故①正确；

②当x＜1时，函数值y随自变量x的减小而减小，故②错误；

③a＞0，b＜0，c＜0，故③错误；

④垂直于y轴的直线与抛物线交于C、D两点，其C、D两点的横坐标分别为s、t，根据二次函数的对称性可知s+t＝2，故④正确；

故答案是：①④．

15．解：由平移的特征知A′B′∥AB，又CD∥AB，

∴A′B′∥CD，同理B′C′∥AD．

∴四边形BEDF为平行四边形．

∵四边形ABCD是菱形，

∴AB＝AD．

∴∠ABD＝∠ADB．

又∵∠A′B′D＝∠ABD，

∴∠A′B′D＝∠ADB．

∴FB′＝FD．

∴四边形B′EDF为菱形，

∵菱形B′EDF与菱形ABCD有一个公共角，

∴此两个菱形对应角相等又对应边成比例．

∴此两个菱形相似．

∴，

∴B′D＝1，

∴平移的距离BB′＝BD﹣B′D＝﹣1．

故答案为：﹣1．

三．解答题（共8小题，满分75分）

16．解：（1）x2﹣4x+2＝0，

x2﹣4x＝﹣2，

x2﹣4x+4＝﹣2+4，即（x﹣2）2＝2，

∴x﹣2＝±，

∴x1＝2+，x2＝2﹣．

（2），

②﹣①×3得：2x＝3，

解得：x＝，

把x＝代入①得：3+y＝2，

解得：y＝﹣1，

∴原方程组的解为：．

（3）原式＝+﹣

＝+﹣

＝．

17．解：（1）甲抽到“绵山风景名胜区”的概率是，

故答案为：；

（2）画树状图如下：

共有12种等可能的结果，甲、乙两人中恰好有一人介绍“张壁古堡”的结果有6种，

∴甲、乙两人中恰好有一人介绍“张壁古堡”的概率为＝．

18．解：（1）∵一元二次方程x2﹣6x+k＝0有两个相等的实数根，

∴Δ＝b2﹣4ac＝（﹣6）2﹣4×1×k＝0，

解得：k＝9．

（2）将k＝5代入原方程得x2﹣6x+5＝0，

∵一元二次方程x2﹣6x+5＝0的两根分别为x1，x2，

∴x1•x2＝5，

∴Rt△ABC的面积＝x1•x2＝．

19．解：（1）在Rt△PCA中，

∵∠CPA＝60°，PA＝60海里，

∴∠A＝30°，

∴PC＝PA＝30海里，AC＝30海里，

在Rt△BCP中，

∵∠CPB＝45°，

∴BC＝PC＝30海里，

∴PB＝30海里；

（2）∵AC＝海里，BC＝30海里，

∴AB＝AC+BC＝（30+30 ）海里．

20．（1）证明：∵∠ACB＝90°，

∴∠BCD+∠ACE＝90°，

∵AE⊥CE，

∴∠AEC＝90°，

∴∠ACE+∠CAE＝90°，

∴∠BCD＝∠CAE，

∵BD⊥DE，

∴∠BDC＝90°，

∴∠BDC＝∠AEC，

∴△BDC∽△CEA；

（2）如图，过点A作AM⊥BC于点M，过点D作DN⊥BC，交BC的延长线于点N，

∴∠AMB＝∠DNC＝90°，

∵四边形ABCD是平行四边形，

∴AB∥CD，AB＝CD，

∴∠B＝∠DCN，

∴△ABM≌△DCN（AAS），

∴BM＝CN，AM＝DN，

∵AB＝AE，AM⊥BC，

∴BM＝ME，

∵BE＝4，EC＝3，

∴BC＝BE+EC＝7，

设DN＝b，

∴BM＝ME＝CN＝2，EN＝5，

∵∠AED＝90°，

由（1）得△AEM∽△EDN，

∴＝，

∴＝，

∴b＝，

∴▱ABCD的面积＝BC•DN＝7．

21．解：（1）设第二批生产的工艺品比第一批增加x件，则工艺品有（50+x）件，座椅有（50﹣x）件，

由题意得：W1＝（50+x）（160﹣2x）＝﹣2x2+60x+8000，

W2＝19（50﹣x）＝﹣19x+950；

（2）根据题意，得：

W＝W1+W2

＝﹣2x2+60x+8000﹣19x+950

＝﹣2x2+41x+8950

＝﹣2（x﹣）2+，

∵﹣2＜0，且x为整数，

∴当x＝10时，W取得最大值，最大值为9160，

答：当x＝10时，第二批生产的工艺品和座椅售完后获得的总利润W最大，最大总利润是9160元．

22．解：把点M（1，2）代入y＝ax2得a＝2；

把点N（3，3）代入y＝ax2得a＝，

如图：

∵如果抛物线y＝ax2（a＞0）与线段MN没有公共点，

∴a的取值范围为0＜a＜或a＞2．

23．解：（1）补充的证明过程如下：

∵AG∥BD，

∴△AGE∽△CDE．

∴，

∴；

（2）根据梅涅劳斯定理得：．

又∵，，

∴DE＝AE．

在Rt△ABD中，AB＝13，BD＝5，∠ADB＝90°，则由勾股定理知：AD＝＝＝12．

∴AE＝6．

故答案是：6．