初中数学湘教版八年级下册1.4 角平分线的性质获奖ppt课件

这是一份初中数学湘教版八年级下册1.4 角平分线的性质获奖ppt课件，文件包含湘教版八下数学14角平分线的性质1课件pptx、湘教版八下数学14角平分线的性质1教案docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。
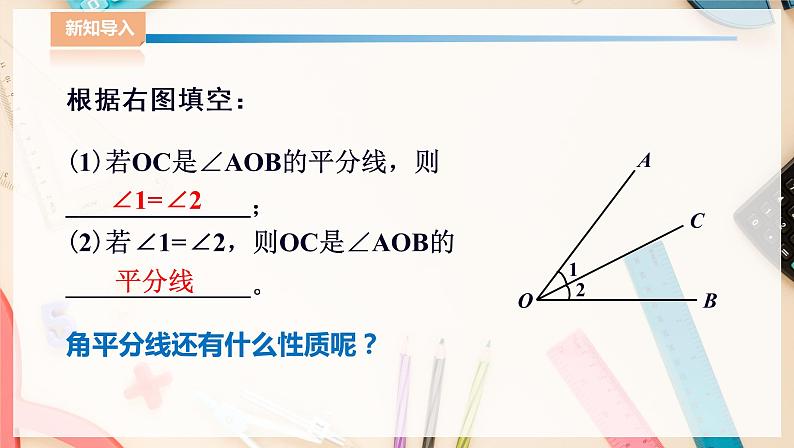
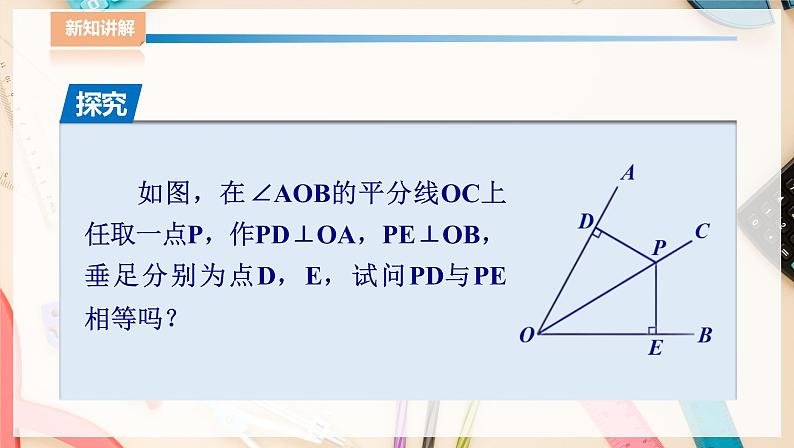
1.4 角平分线的性质(1)教案主备人：                  审核人：                           本章课时序号：7课   题角平分线的性质课型新授课教学目标  1. 通过探究和证明，掌握角平分线的性质定理；  2. 通过合作活动，掌握角平分线性质定理的逆定理；     3. 能利用角平分线的性质定理及逆定理解决简单问题；  4. 增强探究几何结论的能力，培养科学严谨的学习习惯. 教学重点1. 探究角平分线的性质定理和逆定理；2. 利用角平分线的性质定理及逆定理解决简单问题.教学难点1. 探究角平分线的性质定理和逆定理；2. 利用角平分线的性质定理及逆定理解决简单问题. 教   学   活   动一、复习铺垫 1、 回答问题：已知下列条件，如何判定两个直角三角形全等？(1)两个直角三角形的两直角边对应相等.          生答：SAS(2)两个直角三角形的一边和一锐角对应相等.      生答：ASA或AAS (3)两个直角三角形的斜边和一直角边对应相等.    生答：HL(在学生回答时，教师可画图，引导学生理解和记忆).2、 根据右图填空：(1) 若OC是∠AOB的平分线，则    ∠1=∠2    ；             (2) 若∠1=∠2，则OC是∠AOB的    平分线    。3、 导入新课：角平分线还有什么性质呢？二、教学新知（一）角平分线的性质定理1、 出示问题如图，在∠AOB的平分线OC上任取一点P，作PD⊥OA，PE⊥OB，垂足分别为点D，E，试问PD与PE相等吗？2、 合作交流生：将∠AOB沿OC对折，我发现PD与PE重合，即PD与PE相等.师：能证明PD与PE相等吗？3、 证明结论∵ PD⊥OA，PE⊥OB，∴ ∠PDO=∠PEO=90°，在△PDO和△PEO中， ∵ ∠PDO=∠PEO，   ∠DOP=∠EOP，   OP=OP，∴ △PDO≌△PEO.∴ PO=PE.4、 展示结论由此得到角平分线的性质定理：角的平分线上的点到角的两边的距离相等.（二）角平分线的性质定理的逆定理1、 出示问题角的内部到角的两边的距离相等的点在这个角的平分线上 吗？如图，点P在∠AOB的内部，作PD⊥OA，PE⊥OB，垂足分别为点D，E.若PD=PE，那么点P在∠AOB的平分线上吗？2、 合作交流如果点P在∠AOB的平分线上，则过点O，P作射线OP，有∠AOP=∠BOP.因此，只需证明△PDO≌△PEO.如图。3、 证明结论过点O，P 作射线OC，如图.∵ PD⊥OA，PE⊥OB，∴ ∠PDO＝∠PEO＝90°.在Rt△PDO和Rt△PEO中，∵ OP=OP，   PD=PE，∴ Rt△PDO≌Rt△PEO.∴ ∠AOC=∠BOC.∴ OC是∠AOB的平分线，即点P在∠AOB的平分线上.4、 展示结论角平分线的性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上.三、讲解例题，学会方法  例1 如图，∠BAD=∠BCD=90°，∠1=∠2.(1)求证：点B在∠ADC的角平分线上；(2)求证：BD是∠ABC的平分线.分析：(1)由∠1=∠2得BA=BC，根据角平分线性质定理的逆定理即可证明.(2)根据条件可证△BAD≌△BCD，得出∠ABD=∠CBD即可.证明：(1)在△ABC中，∵ ∠1=∠2，∴ BA=BC.又 BA⊥AD，BC⊥CD，∴ 点D在∠ADC的角平分线上.(2)在Rt△BAD和Rt△BCD中，∵ BA=BC，BD=BD.∴ Rt△BAD≌Rt△BCD.∴ ∠ABD=∠CBD.∴ BD是∠ABC的角平分线.四、巩固练习1、 如图，OP为∠AOB的平分线，PD⊥OA，PE⊥OB，下列说法中正确的有（     ）①PD=PE；②OD=OE；③∠DPO=∠EPO；④OC垂直平分线段DE.A. 1个B. 2个C. 3个D. 4个【答案】D2、 如图，在AB上求一点P，使它到∠MON的两边OM，ON的距离相等，则点P是（   ）A. OM与ON的垂直平分线的交点B. 线段AB的中点C. ∠MON的角平分线与AB的交点D. AB的垂直平分线与∠MON的角平分线的交点【答案】C五、课堂总结，深化理解回答问题1、 角平分线的性质定理是什么？PPT：角的平分线上的点到角的两边的距离相等2、 角平分线的性质定理的逆定理是什么？PPT：角的内部到角的两边距离相等的点在角的平分线上.六、作业布置第24页课后练习第1、2题：1、 如图，在直线MN上求作一点P，使点P到∠AOB两边的距离相等。                       提示：作∠AOB的平分线OC，与直线相交，则它们的交点就是所求作的点P.2、 在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，BD=CD. 求证：AB=AC.思路：先由角平分线的性质得出DE=DF；再证明△BDE≌△CDF，得出∠B=∠C.从而可得出AB=AC. 板书设计1.4角平分线的性质1、 角平分线的性质定理：角的平分线上的点到角的两边的距离相等；2、 角平分线的性质定理的逆定理：角的内部到角的两边距离相等的点在角的平分线上.课后反思