1.1集合（精讲）-【题型·技巧培优系列】最新高考数学大一轮复习精讲精练（新高考地区）

1.1  集合

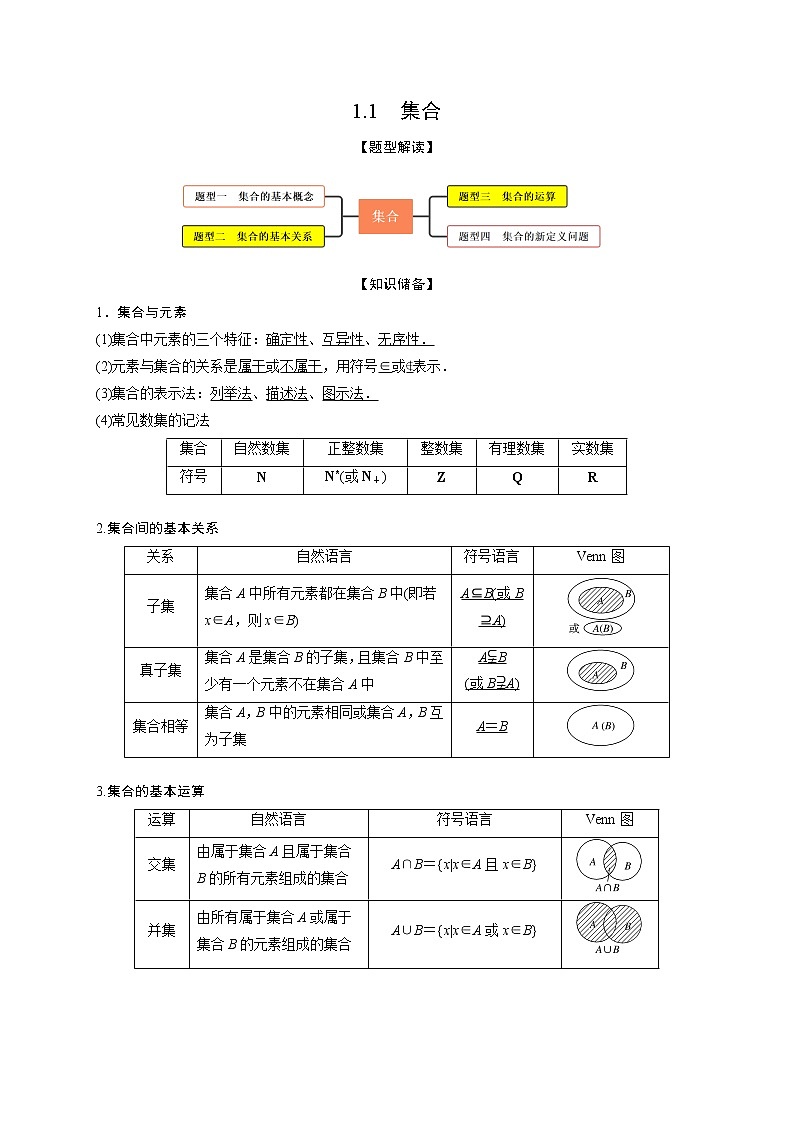
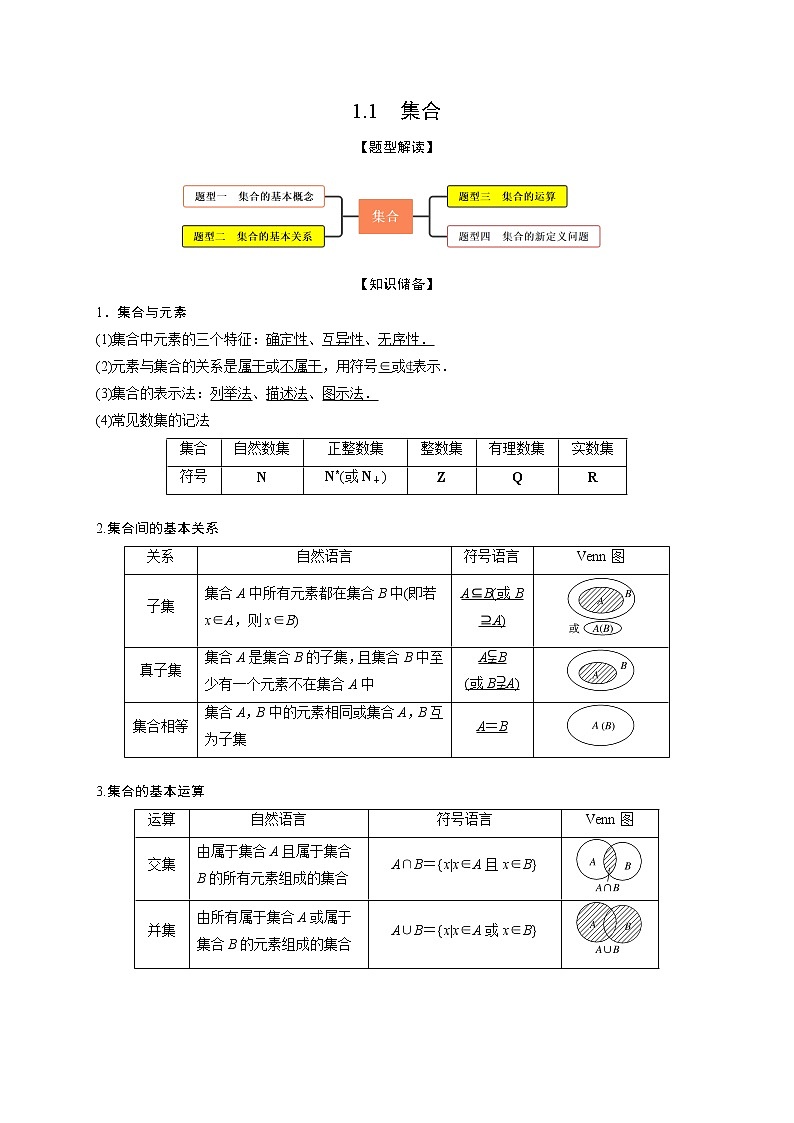
【题型解读】

【知识储备】

1．集合与元素

(1)集合中元素的三个特征：确定性、互异性、无序性．

(2)元素与集合的关系是属于或不属于，用符号∈或∉表示．

(3)集合的表示法：列举法、描述法、图示法．

(4)常见数集的记法

2.集合间的基本关系

3.集合的基本运算

(2)三种运算的常见性质

①A∪B＝A⇔B⊆A，A∩B＝A⇔A⊆B.②A∩A＝A，A∩∅＝∅.

③A∪A＝A，A∪∅＝A.④A∩∁UA＝∅，A∪∁UA＝U，∁U(∁UA)＝A.

⑤A⊆B⇔A∩B＝A⇔A∪B＝B⇔∁UA ⊇∁UB⇔A∩(∁UB)＝∅.

【题型精讲】

【题型一　集合的基本概念】

必备技巧  解决集合概念问题的关键

一是确定构成集合的元素；二是确定元素的限制条件；三是根据元素的特征(满足的条件)构造关系式解决相应问题．特别提醒：含字母的集合问题，在求出字母的值后，需要验证集合的元素是否满足互异性．

例1　（2022·山东济南·二模）已知集合，， ，则C中元素的个数为（       ）

A．1 B．2 C．3 D．4

例2　（2022·武汉校级月考）已知集合A＝{m＋2，2m2＋m}，若3∈A，则m的值为________．

例3　【多选】（2022·全国·高三专题练习）已知集合，若集合A有且仅有2个子集，则a的取值有（       ）

A．-2 B．-1 C．0 D．1

【题型精练】

1. （2022·宁夏银川·一模）已知集合，，则B中所含元素的个数为（       ）

A．2 B．3 C．4 D．6

2．（2022·全国高三课时练习）设A＝，B＝{|a－2|,3}，已知4∈A且4∉B，则a的取值集合为________．

3．（2022·全国高三课时练习）已知集合A＝{x|ax2﹣3x+2＝0，x∈R，a∈R}只有一个元素，则a＝_____．

【题型二　集合的基本关系】

必备技巧  集合的基本关系

(1)空集是任何集合的子集，在涉及集合关系问题时，必须考虑空集的情况，否则易造成漏解．

(2)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、Venn图等来直观解决这类问题．

例4　（2022·广东广州·一模）已知集合，，则的子集个数为（       ）

A．2 B．3 C．4 D．6

例5　（2022·河南·灵宝市第一高级中学模拟预测）已知集合，，则（       ）

A． B．

C． D．

例6　（2022·广西·模拟预测）已知集合，或.

（1）若，求；

（2）若，求a的取值范围.

【题型精练】

1．（2022·湖北武汉摸底）已知集合A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0<x<5，x∈N}，则满足条件A⊆C⊆B的集合C的个数为(　　)

A．1  B．2

C．3  D．4

2. （2022·陕西陕西·二模）已知集合，，若，则实数a的取值范围是（       ）

A． B． C． D．

3. （2022·全国·高三专题练习）集合，，则（       ）

A． B． C．         D．

【题型三　集合的运算】

必备技巧  集合的运算

(1)对于集合的交、并、补运算，如果集合中的元素是离散的，可用Venn图表示；如果集合中的元素是连续的，可用数轴表示，此时要注意端点的情况．

(2)运算过程中要注意集合间的特殊关系的使用，灵活使用这些关系，能简化运算．

例7　（2022·江苏·苏州中学高三开学考试）已知集合A＝，则A∩B＝（       ）

A．(0，2] B．(0，2) C．(1，2] D．(0，＋∞)

例8　（2022·山东·夏津第一中学高三阶段练习）已知集合，，则（       ）

A． B． C． D．

例9　（2022·江苏·高三专题练习）已知集合，则_______________

例10  （2022·浙江·高三专题练习）已知全集，集合，，则下列Venn图中阴影部分的集合为___________．

例11　（2022·全国·高三专题练习）已知集合，，若，则实数的取值范围是___________.

【题型精练】

1．（2022·安徽·芜湖一中一模）已知集合，，则（       ）

A． B． C． D．

2. （2022·全国·高三专题练习（理））若集合，则（       ）

A． B． C． D．

3. （2022·湖南·长沙一中高三阶段练习）如图，已知集合，，，，，则图中的阴影部分表示的集合为（       ）

A．， B．，， C．， D．，，

4. （2022·浙江绍兴·高三期末）已知全集，集合，，则（       ）

A． B． C． D．

5. （2022·全国·高三专题练习）已知集合，，若，则实数的取值集合为（       ）

A． B． C． D．

【题型四  集合的新定义问题】

必备技巧  解决集合新定义问题的关键

(1)准确转化：解决新定义问题时，一定要读懂新定义的本质含义，紧扣题目所给定义，结合题目所给定义，结合题目的要求进行恰当转化，切忌同已有概念或定义相混淆．

(2)方法选取：对于新定义问题，可恰当选用特例法、筛选法、一般逻辑推理等方法，并结合集合的相关性质求解．

(3)从新定义出发，结合集合的性质求解，提升逻辑推理核心素养．

例12　（2022·北京房山·一模）已知U是非实数集，若非空集合A1，A2满足以下三个条件，则称（A1，A2）为集合U的一种真分拆，并规定（A1，A2）与（A2，A1）为集合U的同一种真分拆

①A1∩A2=0

②A1A2=U

③的元素个数不是中的元素.

则集合U={1，2，3，4，5，6}的真分拆的种数是（       ）

A．5 B．6 C．10 D．15

例13　（2022·全国·高三专题练习）设是两个非空集合，定义集合间的一种运算“”：

，如果，，则____________.

【题型精练】

1．（2022·全国·高三专题练习）若一个集合是另一个集合的子集，则称两个集合构成“鲸吞”；若两个集合有公共元素，且互不为对方子集，则称两个集合构成“蚕食”，对于集合，，若这两个集合构成“鲸吞”或“蚕食”，则a的取值集合为_____.

2. （2022·全国·高三专题练习）用表示非空集合A中元素的个数，定义，已知集合，，且，设实数a的所有可能取值构成集合S，则（       ）