专题27.10 由平行线截得的比例线段（巩固篇）（专项练习）-2022-2023学年九年级数学下册基础知识专项讲练（人教版）

这是一份专题27.10 由平行线截得的比例线段（巩固篇）（专项练习）-2022-2023学年九年级数学下册基础知识专项讲练（人教版），共36页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题27.10 由平行线截得的比例线段（巩固篇）（专项练习）
一、单选题
1．如图，已知AB∥CD∥EF，AC＝6，CE＝2，BD＝4，则DF的值为（　　）

A． B． C． D．1
2．如图，，AF交BE于点G，若AC＝CG，AG＝FG，则下列结论错误的是（       ）

A． B． C． D．
3．如图，点G、F分别是的边、上的点，的延长线与的延长线相交于点A，交于点E，则下列结论错误的是（       ）

A． B． C． D．
4．如图，在中，，分别以点A和点C为圆心，大于的长为半径作弧，两弧相交于M，N两点，作直线，直线与相交于点D，连接，若，则的长是（       ）

A．6 B．3 C．1.5 D．1
5．如图，在中，，点D为的中点，∥交于点E，连接，若，，则的长为（       ）

A．12 B．20 C．24 D．26
6．如图，在中，顶点O与原点重合，，，，点C为边OA上一点，且．将向右平移，当点C的对应点恰好落在直线上时，点B的对应点的坐标为（       ）

A． B． C． D．
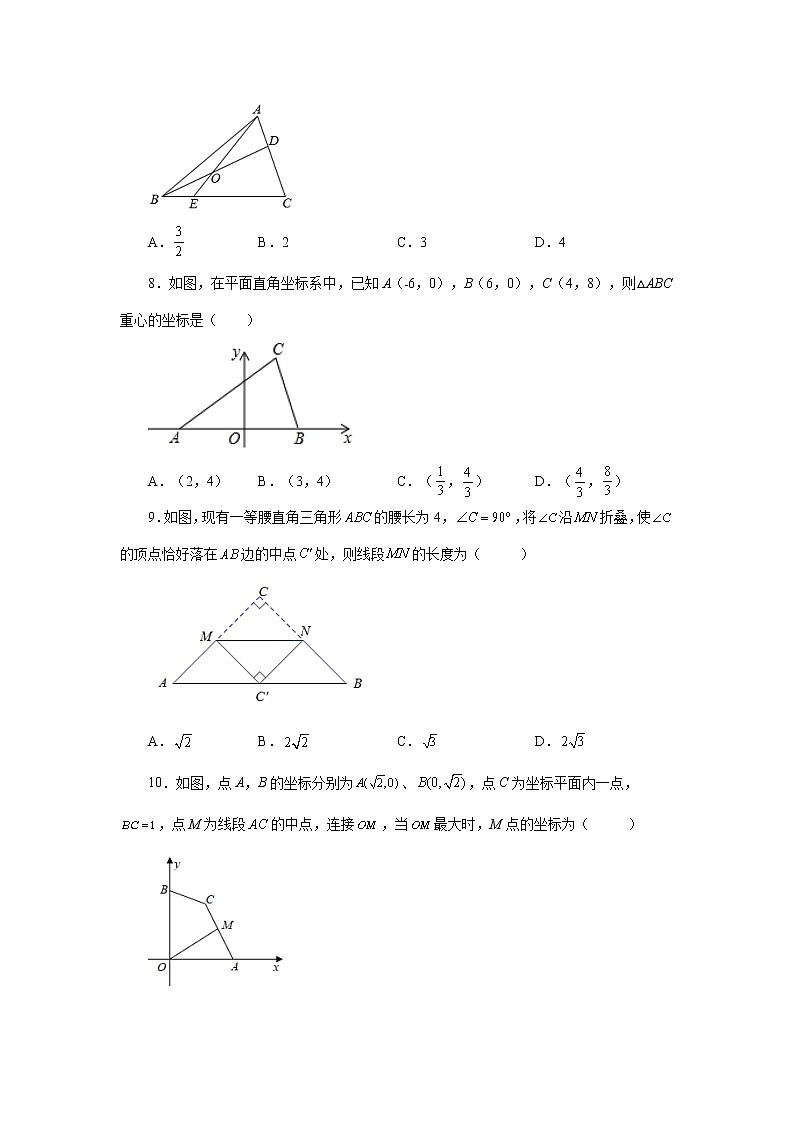
7．如图，在中，D在AC边上，AD:DC=1:2，O是BD的中点，连接AO并延长交BC于E，若BE=1，则EC=（       ）

A． B．2 C．3 D．4
8．如图，在平面直角坐标系中，已知A（﹣6，0），B（6，0），C（4，8），则△ABC重心的坐标是（　　）

A．（2，4） B．（3，4） C．（，） D．（，）
9．如图，现有一等腰直角三角形的腰长为4，，将沿折叠，使的顶点恰好落在边的中点处，则线段的长度为（       ）

A． B． C． D．
10．如图，点A，B的坐标分别为、，点C为坐标平面内一点，，点M为线段的中点，连接，当最大时，M点的坐标为（       ）

A． B． C． D．
二、填空题
11．如图，在△ABC中，∠A=30°，∠B=90°，D为AB中点，E在线段AC上，，则_____．

12．如图，直线CE是平行四边形ABCD的边AB的垂直平分线，垂足为点O，CE与DA的延长线交于点E．连接AC，BE，DO，DO与AC交于点F，则下列结论：
①四边形ACBE是菱形；       ②∠ACD=∠BAE；       ③AF：FC=1：2；
其中正确的结论有________．（填写所有正确结论的序号）

13．如图，已知，三条对应边BC、CE、EF在同一条直线上，连接BG，分别交AC、DC、DE于点P、Q、K，其中，则图中三个阴影部分的面积和为__________．

14．如图，在平行四边形ABCD中，，，，分别以A，C为圆心，大于的长为半径画弧，两弧相交于点M，N，过M，N两点作直线，与BC交于点E，与AD交于点F，连接AE，CF，则四边形AECF的周长为______．

15．在现实生活中，我们经常会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为，我们不妨就把这样的矩形称为“标准矩形”，在“标准矩形”中，如图所示，点在上，且，若为边上一动点，当的周长最小时，则的值为______．

16．如图，在平面直角坐标系内，，的横坐标分别是1和3，线段，，，…都垂直于x轴，且，，，…，等线段互相平行，若，，，…，．都在直线上，则的长度是______．

17．如图，在中，，，将边沿着翻折，使点B落在上的点D处，再将边沿着翻折，使得C落在延长线上的点处，两条折痕与斜边分别交于E，F．

（1）__________．
（2）__________．
18．如图，△ABC是边长为2的等边三角形，AD是BC边上的高，CE是AB边上的高．将△ADC绕点D顺时针旋转得到，其中点A的对应点为点，点C的对应点为点．在旋转过程中，当点落在直线EC上时，的长为______．

三、解答题
19．如图，，直线，交于点，且分别与直线，，交于点，，和点，，，已知，，，，求的长度．






20．已知：如图，线段AB．

求作：点C，D，使得点C，D在线段AB上，且AC=CD=DB．
作法：①作射线AM，在射线AM上顺次截取线段AE=EF=FG，连接BG；
②以点E为圆心，BG长为半径画弧，再以点B为圆心，EG长为半径画弧，两弧在AB上方交于点H；
③连接BH，连接EH交AB于点C，在线段CB上截取线段CD=AC．
所以点C，D就是所求作的点．
(1)使用直尺和圆规，依作法补全图形（保留作图痕迹）；
(2)完成下面的证明．
证明：∵EH=BG，BH=EG，
∴四边形EGBH是平行四边形．（______）（填推理的依据）
∴，即．
∴AC∶______=AE∶AG．
∵AE=EF=FG，
∴AE=______AG．
∴．
∴．
∴AC=CD=DB．
21．如图，在中，点D是AB边上的一点．
(1) 尺规作图：在内，求作，DE交AC于E；（不写作法，保留作图痕迹）
(2) 在（1）的条件下，若，求的值．



22．请阅读以下材料，并完成相应的问题：角平分线分线段成比例定理：如图1，在△ABC中，AD平分∠BAC，则，下面是这个定理的部分证明过程：
证明：如图2，过C作CEDA，交BA的延长线于E．…
任务：
(1) 请按照上面的证明思路，写出该证明的剩余部分；
(2) 如图3，已知Rt△ABC中，AB＝3，BC＝4，∠ABC＝90°，AD平分∠BAC，求BD的长．（请按照本题题干的定理进行解决）




23．如图，在平行四边形ABCD中，AB＝3，点E为线段AB的三等分点（靠近点A），点F为线段CD的三等分点（靠近点C），且CE⊥AB．将△BCE沿CE对折，BC边与AD边交于点G，且DC＝DG．
（1）证明：四边形AECF为矩形；
（2）求四边形AECG的面积．





24．如图，△ABC中，于点D，E是AB上一点，连接DE，．
(1)求证；
(2)若，，求证；
(3)若，，则的值为______（用含m，k的式子表示）．


、













参考答案
1．B
【分析】
根据平行线分线段成比例定理即可得出结论．
解：∵直线AB∥CD∥EF，AC=6，CE=2，BD=4，
∴ 即，解得DF=．
故选：B．
【点拨】此题考查的是平行线分线段成比例定理，熟知三条平行线截两条直线，所得的对应线段成比例是解答此题的关键．
2．B
【分析】
根据平行线分线段成比例定理进行逐项判断即可．
解：∵，
∴，
∵AC＝CG，
∴，
故A正确，不符合题意；
∵，
∴，
∵AG＝FG，
∴BG＝EG，
∴BE＝2BG，
∵，
∴BG＝2DG，
∴BE＝4DG，
∴，
故B错误，符合题意；
∵，
∴，
∵BG＝2DG，BE＝4DG，
∴DE＝3DG，
∴，
故C正确，不符合题意；
∵，
∴，
∵DE＝3DG，
∴EG＝2DG，
∴，
故D正确，不符合题意．
故选：B．
【点拨】本题考查了平行线分线段成比例定理，根据平行线分线段成比例定理逐一分析四个结论的正误是解题的关键．
3．C
【分析】
根据平行线分线段成比例定理对各选项进行判断即可．
解：∵，交GA于点E，
∴，，，，
∴A，B，D正确，不符合题意；
故选C．
【点拨】本题考查了平行线分线段成比例定理．找准对应关系是解题的关键．
4．C
【分析】
由作图可得：是AC的垂直平分线，记MN与AC的交点为G，证明 再证明 可得，从而可得答案．
解：由作图可得：是AC的垂直平分线，记MN与AC的交点为G，

∴
∵，

∴
∴


故选C
【点拨】本题考查的是线段的垂直平分线的性质，平行线分线段成比例，证明是解本题的关键．
5．C
【分析】
根据题意可知为的中位线，根据等腰三角形的性质可得，勾股定理解即可求解．
解：点D为的中点，
，
∥，
，
，
，
，
，
，
在中，，
故选C．
【点拨】本题考查了平行线分线段成比例，三角形中位线的判定与性质，三线合一，勾股定理，求得是中点是解题的关键．
6．B
【分析】
先求得点，的坐标，根据平移后纵坐标相等，求得点的坐标，进而求得平移距离，即可求得点的坐标．
解：如图，过点分别作轴的垂线，垂足分别为，过点作轴，与的延长线交于点，则四边形是矩形，

设，则，


又

，


∵




，

∴





中，

将向右平移，当点C的对应点恰好落在直线上时，

解得

平移

点的对应点的坐标为．
故选B
【点拨】本题考查了坐标与图形，平移的性质，一次函数的性质，平行线分线段成比例，求得点的坐标是解题的关键．
7．C
【分析】
过点D作交BC于F，根据平行线分线段成比例定理可得，，，再根据O是BD的中点，可得BE=EF，进而解答即可．
解：过点D作交BC于F，如图，

∵，
∴，
∵O是BD的中点，
∴BO=OD，
∴BE=EF，
∵，
∴，
∴CF=2EF，
∴BE:EC=BE:3BE=1:3，
∵BE=1，
∴EC=3，
故选：C．
【点拨】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．过分点作平行线构建平行线分线段成比例定理的基本图形是解决问题的关键．
8．D
【分析】
连接OC，如图，先确定△ABC的重心D在OC上，作CE⊥OB于E，DF⊥OB于F，如图，根据三角形重心的性质得OD：OC＝1：3，由于DF∥CE，则＝，然后计算出DF和OF，从而得到D点坐标．
解：连接OC，如图，

∵A（﹣6，0），B（6，0），
∴O点为AB的中点，
∴△ABC的重心D在OC上，
作CE⊥OB于E，DF⊥OB于F，如图，
∵D点为△ABC的重心，
∴CD＝2OD，
∴OD：OC＝1：3，
∵DF∥CE，
∴＝，
而C（4，8），
∴OE＝4，CE＝8，
∴，
∴DF＝，OF＝，
∴D（，）．
故选D．
【点拨】本题主要考查了三角形的重心的性质和相似三角形的判定与性质，解决本题的关键是要熟练掌握三角形的重心的性质和相似三角形的判定与性质．
9．B
【分析】
连接，交MN于点O，可得AB∥MN，根据平行线分线段定理，可得MN是三角形的中位线，进而即可求解．
解：连接，交MN于点O，
∵等腰直角三角形中，的顶点恰好落在边的中点处，
∴⊥AB，⊥MN，，
∴AB∥MN，
∴AM=CM，CN=BN，
∴MN是三角形的中位线，
∵等腰直角三角形的腰长为4，，
∴AB=4，
∴=2．
故选B．

【点拨】本题主要考查等腰直角三角形的性质，平行线分线段成比例定理，折叠的性质，熟练掌握平行线分线段成比例定理是解题的关键．
10．C
【分析】
根据同圆的半径相等可知，点C在半径为1的上运动，取OD=OA，根据三角形的中位线定理知，点C在BD与的交点时，OM最小，在DB的延长线与的交点时，OM最大，根据平行线分线段成比例定理求得C的坐标，进而确定中点M的坐标即可．
解：∵点C在坐标平面内，BC=1，
∴C在半径为1的上，
如图所示，取，连接CD，
∵AM=CM，OD=OA，
∴OM为△ACD的中位线，
∴，
当OM最大时，即CD最大，
此时D，B，C三点共线，
∵，∠BOD=90°，
∴BD=2，
∴CD=2+1=3，
作CE⊥x轴于E点，
∵CE∥OB，
∴，即：，
∴，
∴，
∴，
∵M是AC的中点，
∴，
故选：C．

【点拨】本题考查了坐标与图形的性质，三角形的中位线定理等，确定OM最大时动点C的位置关系是解题关键．
11．或
【分析】
由题意可求出，取AC中点E1，连接DE1，则DE1是△ABC的中位线，满足，进而可求此时，然后在AC上取一点E2，使得DE1＝DE2，则，证明△DE1E2是等边三角形，求出E1E2＝，即可得到，问题得解．
解：∵D为AB中点，
∴，即，
取AC中点E1，连接DE1，则DE1是△ABC的中位线，此时DE1∥BC，，
∴，
在AC上取一点E2，使得DE1＝DE2，则，
∵∠A=30°，∠B=90°，
∴∠C=60°，BC＝，
∵DE1∥BC，
∴∠DE1E2=60°，
∴△DE1E2是等边三角形，
∴DE1＝DE2＝E1E2＝，
∴E1E2＝，
∵，
∴，即，
综上，的值为：或，
故答案为：或．

【点拨】本题考查了三角形中位线的性质，平行线分线段成比例，等边三角形的判定和性质以及含30°角的直角三角形的性质等，根据进行分情况求解是解题的关键．
12．①②③
【分析】
根据菱形的判定方法、平行线分线段成比例定理、直角三角形斜边中线的性质一一判断即可．
解：∵四边形ABCD是平行四边形，
∴，AB=CD，
∵EC垂直平分AB，
∴OA=OB=AB=DC，CD⊥CE，
∵，
∴=，
∴AE=AD，OE=OC，
∵OA=OB，OE=OC，
∴四边形ACBE是平行四边形，
∵AB⊥EC，
∴四边形ACBE是菱形，故①正确，
∵∠DCE=90°，DA=AE，
∴AC=AD=AE，
∴∠ACD=∠ADC=∠BAE，故②正确，
∵，
∴，故③正确，
故答案是：①②③．
【点拨】此题考查平行四边形的性质、菱形的判定和性质、平行线分线段成比例定理等知识，解题的关键是灵活运用所学知识解决问题．
13．26
【分析】
根据全等三角形对应角相等，可以证明，再根据全等三角形对应边相等BC＝CE＝EF，然后利用平行线分线段成比例定理求出GF＝3PC，KE＝2PC，所以PC＝DK，设△DQK的边DK为x，DK边上的高为h，表示出△DQK的面积，再根据边的关系和三角形的面积公式即可求出三部分阴影部分的面积．
解：∵，
∴∠ACB＝∠DEC＝∠GFE，BC＝CE＝EF，
∴，
∴，，
∴，，
又∵，
∴（相似比为1），
设△DQK的边DK为x，DK边上的高为h，
则，整理得，
∴，
S四边形CEKQ，
，
∴三个阴影部分面积的和为：．
故答案为：26．
【点拨】本题考查了全等三角形的性质、平行线分线段成比例等知识点，解题关键是根据平行线分线段成比例定理找到线段间的关系．
14．10
【分析】
根据作图可得，且平分，设与的交点为，证明四边形为菱形，根据平行线分线段成比例可得为的中线，然后勾股定理求得，根据直角三角形中斜边上的中线等于斜边的一半可得的长，进而根据菱形的性质即可求解．
解：如图，设与的交点为，

根据作图可得，且平分，
，
四边形是平行四边形，
，
，
又， ，
，
，
，
四边形是平行四边形，
垂直平分，
，
四边形是菱形，
，，
，
，
为的中点，
中， ，，
，
，
四边形AECF的周长为．
故答案为：．
【点拨】本题考查了垂直平分线的性质，菱形的性质与判定，勾股定理，平行线分线段成比例，平行四边形的性质与判定，综合运用以上知识是解题的关键．
15．
【分析】
先设出矩形的边长，将AQ和CQ表示出来，再通过作对称点确定△AGQ的周长最小时的G点位置后，利用平行线分线段成比例的基本事实的推论建立等式求解即可．
解：设DC=，DQ=AD=x，
∴
∵矩形ABCD，
∴∠D=∠DCB=∠B=90°，，
∴，
如图，作Q点关于BC的对称点E，连接AE交BC于点M，
∴GQ＝GE，CQ=CE=
∴AQ+QG+AG=，
∴当A、G、E三点共线时，△AGQ的周长最小，
此时G点应位于图中的M点处；
∵矩形ABCD中，∠QCG=90°，
∴E点位于QC的延长线上，
∴CE∥AB，
∴，
即，
故答案为：．

【点拨】本题考查了矩形的性质、勾股定理、最短路径、平行线分线段成比例的基本事实的推论等内容，解题关键是能正确找到满足题意的G点位置，同时要牢记平行线分线段成比例的推论，即平行于三角形的一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．
16．
【分析】
根据直线解析式分别求出线段，的长度，利用平行线分线段成比例求出对应的值，并计算的长度，推导一般性规律，进而可得出答案．
解：当时，，
∴，
∴，
当时，，
∴，
∴，
∵，
∴，
∵，
∴，
∴，
当时，，
∴，
∴，

∴推导一般性规律为：，
故答案为：．
【点拨】本题考查了一次函数图象，点的坐标的变化的规律，平行线分线段成比例等知识．根据点的坐标表示出相应线段的长度并推导一般性规律是解题的关键．
17．     45°    
【分析】
设AB=1，则在Rt△ABC中易得AC=，AB=2，根据翻折的性质，可知，，则有∠ABE=∠DAE，∠DAF=∠CAF，∠AEB=∠AED=90°，AB=AD，BE=ED=，，，则即AE⊥BC，=45°，根据AB=AD=1，∠B=90°-∠C=60°，可知△ABD是等边三角形，则BD=AB=2，，又根据，可知，则，则有，则可求．
解：（1）如图，

为便于计算，设AB=1，
∵在Rt△ABC中有，
∴易得AC=，CB=2，，
根据翻折的性质，可知，，
∴∠ABE=∠DAE，∠DAF=∠CAF，∠AEB=∠AED=90°，AB=AD，BE=ED，，，
∴AE⊥BC，=45°，
（2）∵AB=AD=1，，
∴△ABD是等边三角形，则BD=AB=1=AD，，
又∵，
∴，则，
∵AB=AD，BE=DE，
∴AE⊥BC，
∴，
∴，
又∵，AD=1，
∴．
故答案为：45°，．
【点拨】本题考查了全等三角形，解含特殊角的直角三角形、轴对称（折叠）问题以及平行等问题，熟练掌握对折的性质是解答本题的关键．
18．或
【分析】
分两种情况进行讨论，当点落在点C右侧时，当点落在点E左侧时，过点D作交于点，根据勾股定理，中位线定理，平行线分线段成比例定理求出和的长度即可得出答案．
解：当点落在点C右侧时，过点D作交于点，

∵△ABC是边长为2的等边三角形，AD是BC边上的高，CE是AB边上的高，
∴根据等边三角形三线合一可得，
∴，
∵，，
∴，
∴，
∴，
∴，
∵将△ADC绕点D顺时针旋转得到，
∴，
∴，
∴；
当点落在点E左侧时，过点D作交于点，

同理可得，，
∴       ，
故的长为或，
故答案为：或．
【点拨】本题考查了等边三角形的性质，旋转的性质，中位线定理，平行线分线段成比例定理，勾股定理等知识点，熟练掌握相关基础知识，熟练运用相关定理是解本题的关键．
19．
【分析】
由平行线分线段成比例定理得出比例式，即可得出结果．
解：∵b∥c，，，
∴．
∵，
∴．
∵a∥c，
∴．
∴．
∴．
【点拨】本题考查了平行线分线段成比例定理，熟记平行线分线段成比例定理是解决问题的关键．
20．(1)见分析；(2)两组对边分别相等的四边形是平行四边形；AB；．
【分析】
（1）根据要求作出图形即可．
（2）先证明四边形EGBH是平行四边形，再通过平行线分线段成比例定理来解决问题．
解：(1)补全图形如下图所示：

(2)证明：∵EH=BG，BH=EG，
∴四边形EGBH是平行四边形．（两组对边分别相等的四边形是平行四边形）
∴，即．
∴AC∶AB=AE∶AG．
∵AE=EF=FG，
∴AE=AG．
∴．
∴．
∴AC=CD=DB．
故答案为：两组对边分别相等的四边形是平行四边形；AB；．
【点拨】本题考查基本作图，平行四边形的判定和性质及平行线分线段成比例定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
21．(1)作图见分析(2)
【分析】
（1）以D为顶点作即可；
（2）先证明 再利用平行线分线段成比例可得答案.
(1)解：如图，∠ADE为所求作的角；

(2)解：∵∠ADE=∠B
∴， 而，
∴ ．
【点拨】本题考查的是作一个角等于已知角，平行线分线段成比例的应用，熟练的利用尺规作是解本题的关键.
22．(1)见分析；(2)．
【分析】
（1）如图2：过C作CE∥DA．交BA的延长线于E，利用平行线分线段成比例定理得到＝，利用平行线的性质得∠2=∠ACE，∠1=∠E，由∠1=∠2得∠ACE=∠E，所以AE=AC即可证明结论；
（2）先利用勾股定理计算出AC=5，再利用（1）中的结论得到＝，即＝，则可计算出BD=，然后利用勾股定理计算出AD=，从而可得到△ABD的周长．
(1)解：如图2：过C作CE∥DA．交BA的延长线于E，
∵CE//AD，
∴＝，∠2＝∠ACE，∠1＝∠E，
∵AD平分∠BAC
∴∠1＝∠2，
∴∠ACE＝∠E，
∴AE＝AC，
∴＝；
(2)∵AB＝3，BC＝4，∠ABC＝90°，
∴AC＝5，
∵AD平分∠BAC，
∴＝，即＝，
∴BD＝，
∴AD＝＝＝，
∴△ABD的周长＝+3+＝．
【点拨】本题主要考查了平行线分线段成比例定理、平行线的性质、勾股定理、角平分线的定义等知识点，灵活应用相关性质定理成为解答本题关键．
23．（1）见分析；（2）
【分析】
（1）由已知可得AE=AB，CF=CD，能得到AE=CF，AE∥CF，再由CE⊥AB，即可证明四边形AECF为矩形；
（2）由折叠可知B'E=BE=2，求得AB'=1，先证明∠B'=∠B'GA，能得到AB'=AG=1，再由AB'∥CD，得到即，得到B'G=1，能得到△AGB'是等边三角形，所求四边形AECG的面积等于直角三角形EB'C与等边三角形AGB'的差．
（1）证明：∵ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵点E为线段AB的三等分点（靠近点A），
∴AE=AB，
∵点F为线段CD的三等分点（靠近点C），
∴CF=CD，
∴AE=CF，
又∵AE∥CF，
∴四边形AECF为平行四边形，
∵CE⊥AB，
∴四边形AECF为矩形；
（2）∵AB=3，
∴AE=CF=1，BE=2，
∵将△BCE沿CE对折得到△ECB'，
∴B'E=BE=2，
∴AB'=1，
∵DC=DG=3，
∴∠DGC=∠DCG，
∵BB'∥CD，
∴∠DCG=∠B'，
∴∠B'=∠DGC，
∵∠DGC=∠B'GA，
∴∠B'=∠B'GA，
∴AB'=AG=1，
∴DA=BC=B'C=4，
∵AB'∥CD，
∴，
∴，
∴B'G=1，
∴△AGB'是等边三角形，
∴A B'=AG=B'G=1，
作GH⊥A B'于H，

则AH=A B'=，
∴GH=，
在Rt△BCE中，BC=4，BE=2，
∴EC==2，
∴S四边形AECG=S△EB'C-S△AB'G=．
【点拨】本题考查平行四边形的性质，矩形的判定，等边三角形的判定与性质，勾股定理，平行线分线段成比例定理；利用平行线分线段成比例定理，确定△AGB'是等边三角形是解本题的关键．
24．(1)见分析；(2)见分析；(3)．
【分析】
（1）由，得到，即，由，得＝2（90°－∠C），结论得证；
（2）在BD上取点F，使，则CF＝2CD，连接AF，过点B作AF的平行线与DE延长线交于点G．先证△AFC是等腰三角形，得，，再证，则，，进一步证得 ，得，则BE＝CF，结论得证；
（3）在BD上取点M，使DM＝DC，连接AM，过点E作EHAM与 BD交于点H．先证明△AMC是等腰三角形，得到∠MAC＝2∠CAD，∠AMC＝∠C，进一步得到∠MAC＝∠BDE，再证△DEH是等腰三角形，DE＝DH，由EHAM，，得到＝，得到，结合，进一步推导出DE＝，即可得到答案．
(1)证明：∵，
∴，
∴，
∴，
∵，
∴＝2（90°－∠C），
∴；
(2)证明：如图1，在BD上取点F，使，则CF＝2CD，连接AF，过点B作AF的平行线与DE延长线交于点G．

∵，，
∴AD垂直平分CF，
∴，
∴△AFC是等腰三角形，
∴，，
∵，
∴，
∵，
∴，
∴∠C＝∠GBD，
又∵，
∴（ASA），
∴，，
∴，
∵，，
∴∠C＝∠BEG，
∴，
∴，
∴BE＝CF，
∵，
∴．
(3)解：如图2，在BD上取点M，使DM＝DC，连接AM，过点E作EHAM与 BD交于点H．

∵DM＝CD，，，
∴AD垂直平分MC，
∴AM＝AC，
∴△AMC是等腰三角形，
∴∠MAC＝2∠CAD，∠AMC＝∠C，
∵，
∴∠MAC＝∠BDE，
∵EHAM，
∴∠EHD＝∠AMC＝∠C，
∴∠EHD＋∠BDE＋∠HED＝180°，∠AMC＋∠MAC＋∠C＝180°，
∴∠HED＝∠C，
∴∠HED＝∠EHD，
∴△DEH是等腰三角形，
∴DE＝DH，
∵EHAM，，
∴，
∴，
∵，
∴BH＋HM＝BH＋kBH＝（k＋1）BH，BH＋HM＝BD－DM＝BD－CD＝mCD－CD＝（m-1）CD，
∴（k＋1）BH＝（m-1）CD，
∴BH＝，HM＝，
∴DE＝DH＝HM＋DM＝＋CD＝，
∴＝，
即＝
故答案为：．
【点拨】此题考查了等腰三角形的判定和性质、平行线的性质、垂直平分线的性质、全等三角形的判定和性质、平行线分线段成比例定理等知识，添加适当的辅助线是解决问题的关键．