初中数学湘教版八年级下册2.4 三角形的中位线试讲课ppt课件

这是一份初中数学湘教版八年级下册2.4 三角形的中位线试讲课ppt课件，文件包含湘教版八下数学24三角形的中位线课件pptx、湘教版八下数学24三角形的中位线教案docx等2份课件配套教学资源，其中PPT共22页， 欢迎下载使用。
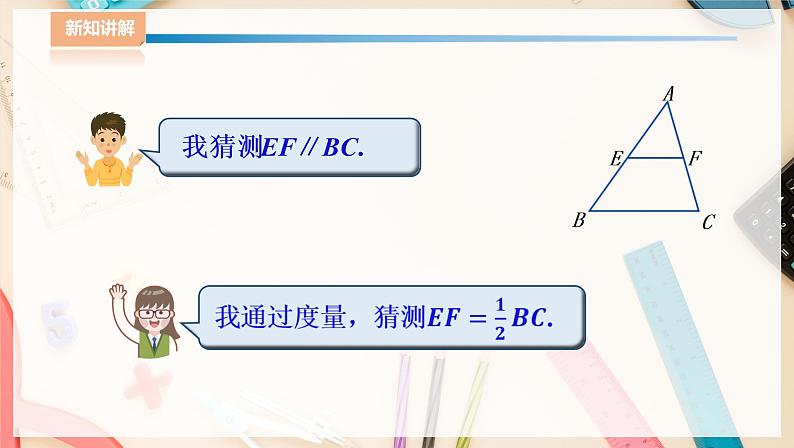
2.4 三角形的中位线教案主备人：                审核人：                           本章课时序号：9课   题三角形的中位线课型新授课教学目标  1. 理解三角形的中位线的概念；  2. 掌握三角形的中位线定理；  3. 能运用三角形的中位线定理解答几何问题；  4. 提高分析问题、逻辑推理能力，激发学习积极性. 教学重点1. 推导三角形的中位线定理；2. 三角形中位线定理的运用。教学难点1. 推导三角形的中位线定理；2. 综合运用三角形中位线定理和平行四边形的性质解决问题。 教   学   活   动一、温故知新 师问生答，PPT展示问题：下图中，D是△ABC的边BC的中点。结合图形说说什么是三角形的中线吗？三角形的一条中线把一个三角形分成两个怎样的三角形？三条中线的交点叫作什么？生1：像△ABC中的线段AD那样，连接三角形的顶点与对边的中点的线段叫作三角形的中线.生2：三角形的一条中线把一个三角形分成面积相等的两个三角形.生3：三角形的三条中线交于一点，这一点叫作三角形的重心.二、教学新知（一）观察图形，理解概念问题：下图中，点E，点F分别是△ABC的边AB，AC的中点.连接EF，我们把EF叫作△ABC的中位线。你能由此抽象出三角形的中位线的概念吗？PPT：连接三角形两边中点的线段叫作三角形的中位线.显然，三角形的中位线与三角形的中线是不同的线段.师：三角形有三条中位线.如图，D，E，F分别是△ABC的三边的中点，所以DF，DF，DF分别是三角形的中位线.（二）师生互动，探究定理问题：如图，EF是△ABC的一条中位线.EF∥BC吗？量一量EF与BC的长各是多少？你能猜测EF与BC具有怎样的位置关系和数量关系吗？为什么？1、 观察、操作与猜测生1：我猜测EF∥BC.生2：我通过度量，猜测EF=BC.2、 讨论证明方法生1：如图，我们可以延长EF至点G，使EF=FG，连接CG，构造△CGF，证明△CGF≌△AEF；再利用全等三角形的性质，证明BE∥CG，BE=CG，从而得四边形BCGE是平行四边形；最后由平行四边形的性质，即可得出猜测成立.生2：我们也可以将△AEF绕点F旋转180°，根据旋转的性质得出有关的线段和角相等，从而得出四边形BCGE是平行四边形。再由平行四边形的性质，得出猜测成立.3、 引导学生证明如图，将△AEF绕点F旋转180°，设点E的像为点G，易知点A的像是点C，点F的像还是点F，且E，F，G在一条直线上.由于旋转不改变图形的形状和大小，所以有CG=AE=BE，GF=EF，∠G=∠AEF.则   EA∥CG，即   BE∥CG.∴ 四边形BCGF是平行四边形.∴ EG∥＝BC.又∵ EF=FG，∴  EF=FG=BC。从而  EF∥＝BC.4、 概括、展示定理三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半.三、讲解例题  例  如图，顺次连接四边形ABCD各边中点E，F，G，H，得到的四边形EFGH是平行四边形吗？为什么？    分析： 由四边形ABCD各边中点想到，可以作辅助线构造三角形，利用三角形的中位线性质来说明四边形EFGH是平行四边形.解：连接AC.∵ EF是△ABC的一条中位线，∴ EF∥AC，且EF=AC又∵ HG是△ABC的一条中位线，∴ HG∥AC，且HG=AC∴ EF∥HG，且EF=HG.∴ 四边形EFGH是平行四边形.四、巩固练习1、 如图，在△ABC中，D，E，F分别是边AB，BC，CA的中点，AB=8cm，BC=6cm，CA=5cm，则四边形ADEF的周长是（    ）A. 11cmB. 13cmC. 14cmD. 19cm【答案】A2、 如图，已知DE是△ABC的中位线，过点C作CF∥BD交DE的延长线于点F，则下列结论不正确的是（    ）A. DE=EFB. AD=DEC. BD=CFD. BC=FD【答案】B3、 如图，□ABCD的对角线AC，BD相交于点O，OE∥AB，下列判断中正确的是（      ）A. AD=2OEB. AC=2OEC. BD=2OED. CD=2OE【答案】D                           五、课堂总结师问生答，展示要点1、 什么叫作三角形的中位线？PPT：连接三角形两边中点的线段叫作三角形的中位线.2、 什么叫作三角形的中位线定理？PPT：三角形的中位线平行于第三边，并且等于第三边的一半.六、作业指导第56页课后练习第1、2题：1、 已知△ABC各边的长度分别为3cm，3.4cm，4cm，求连接各边中点所构成的△DEF的周长.解 △DEF的周长=×(3+3.4+4)=5.2(cm)2、 如图，△ABC的边AB，BC，CA的中点分别是D，E，F.(1)四边形ADEF是平行四边形吗？为什么？(2)四边形ADEF的周长等于AB+AC吗？为什么？解：(1)∴  EF∥AB，且EF=AB=AD∴ 四边形EFGH是平行四边形.(2)∵ 四边形EFGH是平行四边形，∴ AD=EF，BD=AF.∴ 四边形EFGH的周长=2AD+2AF=AB+AC.中心，故连接两组对应点的连线的交点即为对称中心。板书设计2.4三角形的中位线1、 三角形的中位线概念2、 三角形的中位线定理及其应用课后反思