



初中数学人教版七年级下册5.3.1 平行线的性质优质课件ppt
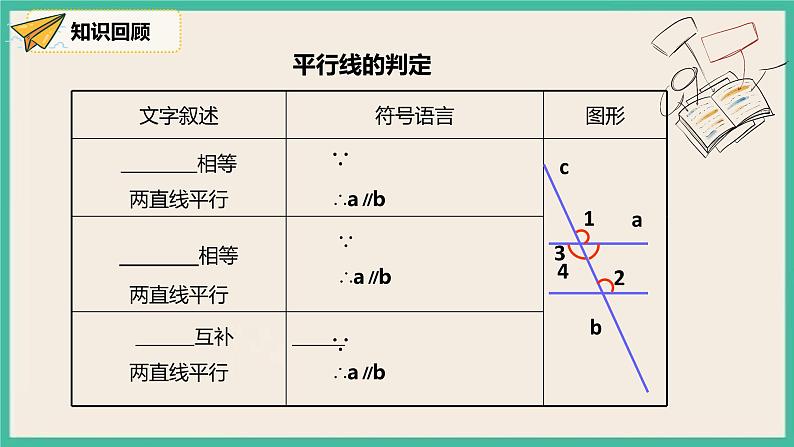
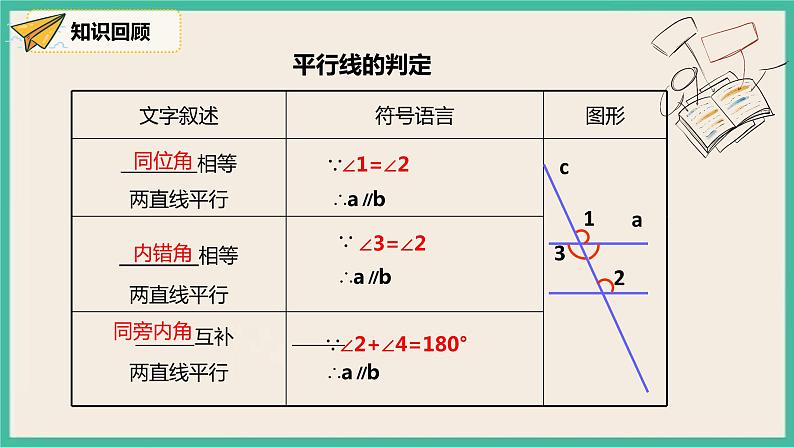
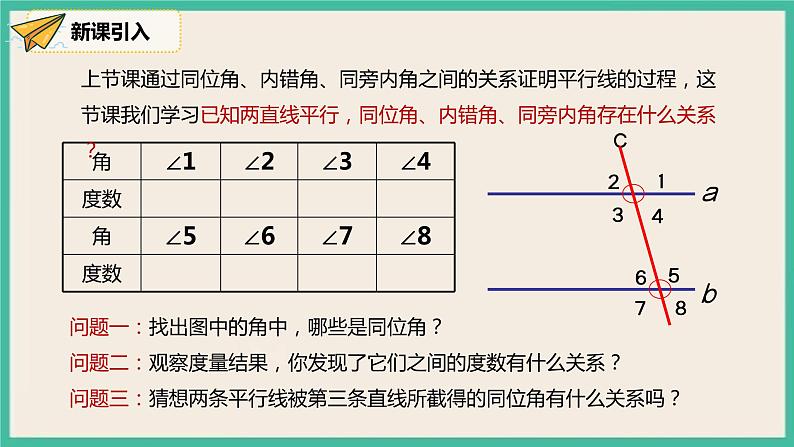
展开平行线的性质人教版数学 七年级下册学习目标01理解平行线的性质。能初步运用平行线的性质进行有关计算。 体会“观察-猜想-证明”的探索方法,培养学生辩证和逻辑能力。知识回顾02∵∵b4平行线的判定同位角内错角同旁内角∵∠1=∠2∠3=∠2∵∠2+∠4=180°平行线的判定新课教学03问题一:找出图中的角中,哪些是同位角?问题二:观察度量结果,你发现了它们之间的度数有什么关系?问题三:猜想两条平行线被第三条直线所截得的同位角有什么关系吗?上节课通过同位角、内错角、同旁内角之间的关系证明平行线的过程,这节课我们学习已知两直线平行,同位角、内错角、同旁内角存在什么关系? 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 选几组同位角,度量这些角,把结果填入下表:问题四:任意画一条截线d,同样度量并比较各对同位角的度数,猜想还成立吗?平行线性质1两条平行线被第三条直线所截,同位角相等。简写为:两直线平行,同位角相等。几何描述:∵ a∥b (已知)∴ ∠1=∠2 (两直线平行,同位角相等)如果两条平行线被第三条直线所截,那么内错角之间有什么关系呢?∵ a∥b(已知)∴ ∠2=∠1(两直线平行,同位角相等)而∠2=∠3 (对顶角相等)∴ ∠1=∠3(等量代换)如图,已知a∥b ,试证明∠1与∠3之间的关系.平行线性质2两条平行线被第三条直线所截,内错角相等。简写为:两直线平行,内错角相等。几何描述:∵ a∥b (已知)∴ ∠1=∠2 (两直线平行,内错角相等)如果两条平行线被第三条直线所截,那么同旁内角之间有什么关系呢?∵ a∥b (已知)∴ ∠2=∠1(两直线平行,同位角相等)而∠2+∠3 =180°∴ ∠1+∠3 =180°(等量代换)如图,已知a∥b ,探究∠1与∠3之间的关系.平行线性质3两条平行线被第三条直线所截,同旁内角互补。简写为:两直线平行,同旁内角互补。几何描述:∵ a∥b (已知)∴ ∠1+∠3 = 180° (两直线平行,同旁内角互补)小试牛刀04 B2.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为( )A.50° B.45° C.30° D.40°C3.如图,已知CD ∥ BE, 如果∠1=60°, 那么∠B的度数为( )A.70° B.100° C.110° D.120°D B5.如图,∠BCD=95°,AB∥DE,则∠α与∠β 满足( )A.∠α+∠β=95° B.∠β﹣∠α=95°C.∠α+∠β=85° D.∠β﹣∠α=85°D延伸拓展05如下图一块梯形贴片的残余部分,量的∠A=100°,∠B=115°,另外两个角分别是多少度?ABCD解:∵该四边形ABCD是梯形 ∴AB∥CD ∴∠A+∠D=180° ∠B+∠C=180°(两直线平行,同旁内角互补) ∴ ∠D=180°- ∠A = 180°- 100°=80° ∠C=180°- ∠B = 180°- 115°=65° 答:梯形的另外两个角分别是80°、65°课堂小结06判定:已知角的关系得平行的关系. 推平行,用判定.性质:已知平行的关系得角的关系. 知平行,用性质.平行线的“判定”与“性质”有什么不同a//b两直线平行同位角相等a//b两直线平行内错角相等同旁内角互补a//b两直线平行平行线的性质∠1=∠2∠3=∠2∠2+∠4=180 °图形已知结果依据
数学七年级下册5.3.1 平行线的性质评优课ppt课件: 这是一份数学七年级下册5.3.1 平行线的性质评优课ppt课件,共18页。PPT课件主要包含了两直线平行,同位角相等,你能得出什么结论呢,性质1,符号语言表示,性质2,∵ab已知,性质3,解∵EF∥AD,∴∠2∠3等内容,欢迎下载使用。
七年级下册5.3.1 平行线的性质教学ppt课件: 这是一份七年级下册5.3.1 平行线的性质教学ppt课件,共17页。PPT课件主要包含了知识要点,下图的线段平行吗,同位角,内错角,同旁内角,平行线的性质,应用格式,∵a∥b已知,∠CPE,等量代换等内容,欢迎下载使用。
数学七年级下册5.3.1 平行线的性质一等奖ppt课件: 这是一份数学七年级下册5.3.1 平行线的性质一等奖ppt课件,文件包含人教版七年级下册531平行线的性质课件pptx、人教版七年级下册531平行线的性质练习题docx、人教版七年级下册531平行线的性质教案docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













