河南省郑州外国语学校2023届高三数学12月调研考试试卷（Word版附答案）

这是一份河南省郑州外国语学校2023届高三数学12月调研考试试卷（Word版附答案），共8页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
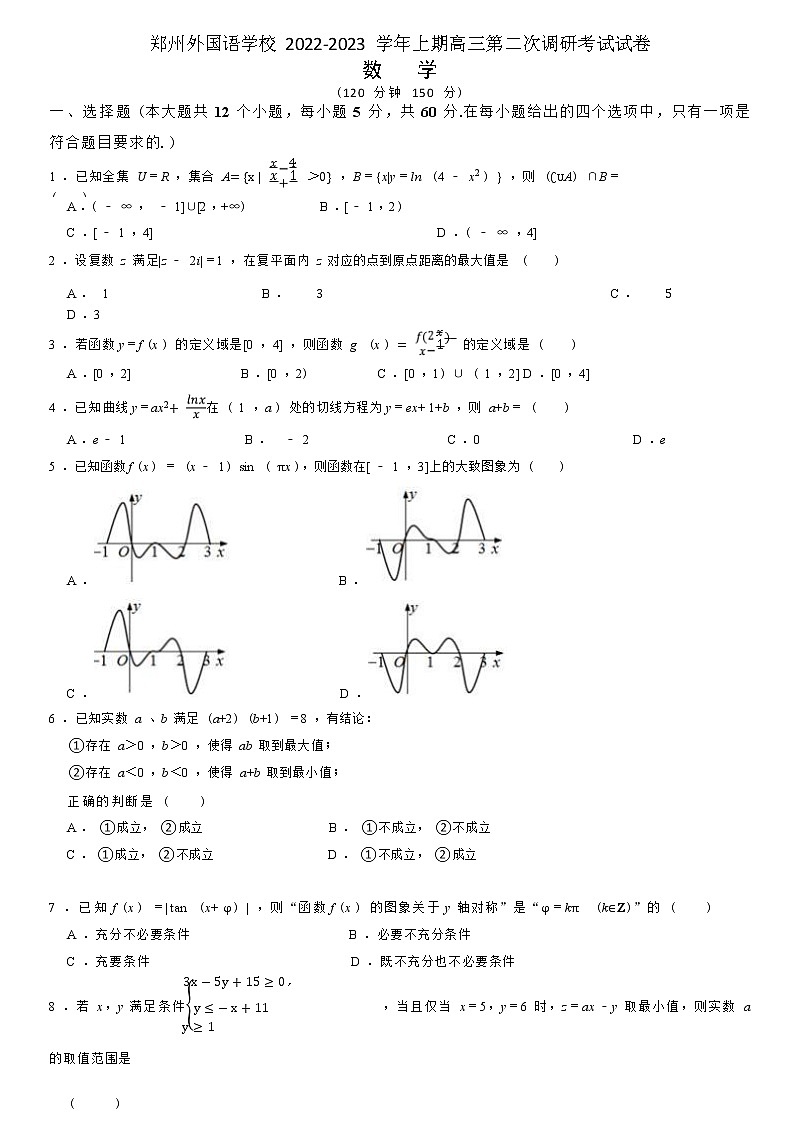
郑州外国语学校 2022-2023 学年上期高三第二次调研考试试卷数   学(120 分钟 150 分)一、选择题 (本大题共 12 个小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有一项是符合题目要求的. )  A ．( ﹣ ∞ ，  ﹣ 1]∪[2 ，+∞)                B ．[ ﹣ 1 ，2 )C ．[ ﹣ 1 ，4]                                                            D ．( ﹣ ∞ ，4]2 ．设复数 z 满足|z ﹣ 2i|＝1 ，在复平面内 z 对应的点到原点距离的最大值是 (    )A ． 1                               B ．   3                                  C ．   5                               D ．33 ．若函数y＝f (x ) 的定义域是[0 ，4] ，则函数 g  (x ) = 1x)  的定义域是 (    )A ．[0 ，2]                      B ．[0 ，2)           C ．[0 ，1) ∪ ( 1 ，2] D ．[0 ，4]4 ．已知曲线y＝ax2+ 在 ( 1 ，a ) 处的切线方程为y＝ex+ 1+b ，则 a+b＝ (    )A ．e ﹣ 1                         B ．  ﹣ 2                            C ．0                               D ．e5 ．已知函数f (x ) ＝ (x ﹣ 1) sin  ( πx )，则函数在[ ﹣ 1 ，3]上的大致图象为 (    )A ．                 B ．C ．                 D ．6 ．已知实数 a 、b 满足 (a+2) (b+1) ＝8 ，有结论：①存在 a＞0 ，b＞0 ，使得 ab 取到最大值；②存在 a＜0 ，b＜0 ，使得 a+b 取到最小值；正确的判断是 (    )A ． ①成立， ②成立                     B ． ①不成立， ②不成立C ． ①成立， ②不成立                   D ． ①不成立， ②成立 7 ．已知f (x ) ＝|tan  (x+ φ) | ，则“函数f (x ) 的图象关于y 轴对称”是“φ＝kπ  (k∈Z)”的 (    )A ．充分不必要条件                       B ．必要不充分条件C ．充要条件                             D ．既不充分也不必要条件8 ．若 x，y 满足条件y ≤ − x + 11               ，当且仅当 x＝5，y＝6 时，z＝ax ﹣y 取最小值，则实数 a 的取值范围是(    )A ．( ﹣ 1 ，)                             B ．( − ，1)               
3C ．( ﹣ 1 ， )5
D ．( ﹣ ∞ ，  ﹣ 1) ∪ ( ，+∞)
9 ．“提丢斯数列”，是由 18 世纪德国数学家提丢斯给出，具体如下：0 ，3 ，6 ，12 ，24 ，48 ，96 ，192 ， … ，容易发 现，从第 3 项开始，每一项是前一项的 2 倍；将每一项加上 4 得到一个数列：4，7，10，16，28，52，100，196，…； 再将每一项除以 10 后得到：“提丢斯数列”：0.4 ，0.7 ，1.0 ，1.6 ，2.8 ，5.2 ，10.0 ， … ，则下列说法中，正确的是               (    )A ．“提丢斯数列”是等比数列 B ．“提丢斯数列”的第 99 项为 C ．“提丢斯数列”前 31 项和为     +D ．“提丢斯数列”中，不超过 20 的有 9 项10．若实数 a ，b 满足ln(2a) − lnb ≥ a2 + − 1 ，则 a+b＝ (    ) 
 2A．2
B ． 2
3  2C．2
D ．2  2
11．在长方体 ABCD ﹣ A1B1C1D1 中，AD＝DD1＝1 ，AB =   3，E，F，G 分别是棱 AB ，BC，CC1 的中点，P 是底面 ABCD 内一动点，若直线 D1P 与平面 EFG 平行，则当三角形 BB1P 面积最小值时，三棱锥 A ﹣ BB1P 的外接球的 表面积为 (    )A ．2π                       B ．3π                         C ．4π                       D ．7π12． 若关于 x 的不等式 ex ≥a  (x2  ﹣ xlnx ) 对任意 x∈  (0 ，+∞) 恒成立，则实数 a 的取值范围是 (     )A ．( ﹣ ∞ ，e2]              B ．( ﹣ ∞ ，e]                  C ．( ﹣ ∞ ， 1]               D ．( − ∞ ， ]二、填空题 (每题 5 分，满分 20 分，将答案填在答题纸上. )13．已知直线 ax+y ﹣ 2+a＝0 在两坐标轴上的截距相等，则实数 a ＝    ．14．已知函数f(x) =   则f(x)＜的解集是   ．15．若直线 ax ﹣y＝0  (a ≠0) 与函数f(x) = 2clnos1 图象交于不同的两点 A ，B ，且点 C  (6 ，0)，若点 D  (m ，n )→                   →                  →                   → 16．若关于 x 的方程 (lnx ﹣ ax ) lnx＝x2 存在三个不等实根，则实数 a 的取值范围是    ．   三、解答题 (本大题共 6 小题，共 70 分.  解答应写出文字说明、证明过程或演算步骤. )17．已知f ( α ) ＝ (  11ssiinnaa +    11ssiinnaa) cos3 α+2sin  (  2几 +α) cos  (  23几 +α) ( α 为第三象限角)．( Ⅰ ) 若 tanα＝2 ，求f ( α ) 的值；( Ⅱ ) 若f ( α ) = 2cosα ，求 tanα的值．
       18．已知等比数列{an}的各项均为正数，且 2an an+1  = 4n (n ∈ N ∗ )．(1) 求数列{an}的通项公式；(2) 设{an}的前 n 项和为 Sn ，max {a ，b}表示 a 与 b 的最大值，记 bn＝max{an ，Sn ﹣ 7} ，求数列{bn }的前 n 项和Tn．19．某同学大学毕业后，决定利用所学专业进行自主创业，经过市场调查，生产一小型电子产品需投入固定成本 2x2  + 2x ，0＜x＜7 x为 6 元，假设该同学生产的商品当年能全部售完．(1) 写出年利润f (x ) (万元) 关于年产量 x 万件的函数关系式；(注：年利润＝年销售收入 ﹣ 固定成本 ﹣ 流动 成本)(2) 当年产量约为多少万件时，该同学的这一产品所获年利润最大？最大年利润多少？  (注：取 e3 ≈20) 20．如图，在四棱锥 P ﹣ ABCD 中，平面 PAD⊥平面 ABCD，PA＝PD，AB＝AD，PA⊥PD，AD⊥CD ，∠BAD＝60°， M，N 分别为 AD ，PA 的中点．( Ⅰ ) 证明：平面 BMN∥平面 PCD；( Ⅱ ) 若AD = 4 ，CD =    3 ，求平面 BMN 与平面 BCP 所成锐二面角的余弦值.  21．在①  (a+c ) ( sinA ﹣ sinC) ＝b ( sinA ﹣ sinB)；② 2ba − =  0 ；③向量m→ = (c ，  3b)与n→ = (cosC ，sinB) 平行，这三个条件中任选一个，补充在下面题干中，然后解答问题．已知△ABC 内角 A ，B ，C 的对边分别为 a ，b ，c ，且满足_______．(1) 求角 C；(2) 若△ABC 为锐角三角形，且 a＝4 ，求△ABC 面积的取值范围．
    22．函数f (x ) ＝ex ，g  (x ) ＝sinx．(1) 求函数y= 的单调递增区间；(2) 当 x∈[0 ，π]时，g  (x ) ﹣ tln  (x+ 1) +2≤2f (x )，求实数 t 的取值范围．