重庆市巫山大昌中学校2021-2022学年高二数学上学期期末试题（Word版附解析）

这是一份重庆市巫山大昌中学校2021-2022学年高二数学上学期期末试题（Word版附解析），共22页。试卷主要包含了请将答案正确填写在答题卷上.等内容，欢迎下载使用。
注意事项：1．答题前在答题卷上填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卷上.
一、选择题（每小题5分，共60分.注意：9至12题为多选题.）
1. 过点，的直线的斜率等于1，则m的值为（ ）
A. 1B. 4C. 1或3D. 1或4
【答案】A
【解析】
【分析】解方程即得解.
【详解】由题得.
故选：A
【点睛】本题主要考查斜率的计算，意在考查学生对该知识的理解掌握水平.
2. 若圆的半径为，则实数（ ）
A. B. -1C. 1D.
【答案】B
【解析】
【分析】将圆的方程化为标准方程，即可求出半径的表达式，从而可求出的值.
【详解】由题意，圆的方程可化为，
所以半径为，解得.
故选：B.
【点睛】本题考查圆的方程，考查学生的计算求解能力，属于基础题.
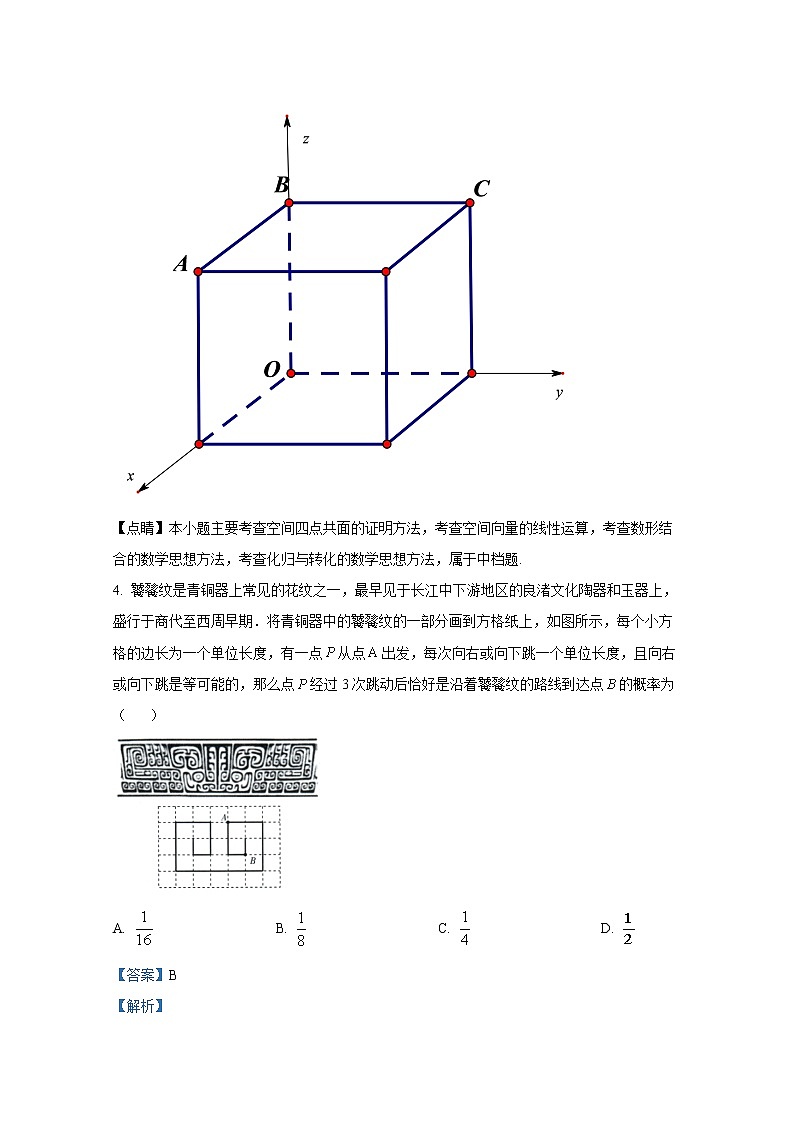
3. 已知A，B，C三点不共线，O是平面ABC外一点，下列条件中能确定点M与点A，B，C一定共面的是
A. B.
C. D.
【答案】D
【解析】
【分析】首先利用坐标法，排除错误选项，然后对符合的选项验证存在使得，由此得出正确选项.
【详解】不妨设.
对于A选项，，由于的竖坐标，故不在平面上，故A选项错误.
对于B选项，，由于的竖坐标，故不在平面上，故B选项错误.
对于C选项，，由于的竖坐标，故不在平面上，故C选项错误.
对于D选项，，由于的竖坐标为，故在平面上，也即四点共面.下面证明结论一定成立：
由，得，
即，故存在，使得成立，也即四点共面.
故选：D.
【点睛】本小题主要考查空间四点共面的证明方法，考查空间向量的线性运算，考查数形结合的数学思想方法，考查化归与转化的数学思想方法，属于中档题.
4. 饕餮纹是青铜器上常见的花纹之一，最早见于长江中下游地区的良渚文化陶器和玉器上，盛行于商代至西周早期．将青铜器中的饕餮纹的一部分画到方格纸上，如图所示，每个小方格的边长为一个单位长度，有一点从点出发，每次向右或向下跳一个单位长度，且向右或向下跳是等可能的，那么点经过3次跳动后恰好是沿着饕餮纹的路线到达点的概率为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】利用古典概型的概率求解.
【详解】解：点从点出发，每次向右或向下跳一个单位长度，跳3次，
则样本空间{（右，右，右），（右，右，下），（右，下，右），（下，右，右），（右，下，下），（下，右，下），（下，下，右），（下，下，下）}，
记“3次跳动后，恰好是沿着饕餮纹的路线到达点B”为事件，则{（下，下，右）}，由古典概型的概率公式可知．
故选：B．
5. 点到直线的距离为
A. 1B. 2C. 3D. 4
【答案】B
【解析】
【分析】直接利用点到直线的距离公式得到答案.
【详解】 ，答案为B
【点睛】本题考查了点到直线的距离公式，属于简单题.
6. 紫砂壶是中国特有的手工制造陶土工艺品,其制作始于明朝正德年间.紫砂壶的壶型众 多,经典的有西施壶、掇球壶、石瓢壶、潘壶等.其中,石瓢壶的壶体可以近似看成一 个圆台 (即圆锥用平行于底面的平面截去一个锥体得到的).下图给出了一个石瓢壶的相关数据(单位:cm),那么该壶的容量约为（ ）
A. 100B.
C. 300D. 400
【答案】B
【解析】
【分析】
根据圆台的体积等于两个圆锥的体积之差，即可求出．
【详解】设大圆锥的高为，所以，解得．
故．
故选：B．
【点睛】本题主要考查圆台体积的求法以及数学在生活中的应用，属于基础题．
7. （2017新课标全国Ⅲ理科）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为
A. B.
C. D.
【答案】B
【解析】
【详解】绘制圆柱的轴截面如图所示，由题意可得：，
结合勾股定理，底面半径，
由圆柱的体积公式，可得圆柱的体积是，故选B.
【名师点睛】涉及球与棱柱、棱锥的切、接问题时，一般过球心及多面体中的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题，再利用平面几何知识寻找几何体中元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解.
8. 已知圆，圆，M，N分别是圆上的动点，P为x轴上的动点，则以的最小值为（ ）
A B. C. D.
【答案】A
【解析】
【分析】求出圆关于轴的对称圆的圆心坐标，以及半径，然后求解圆与圆的圆心距减去两个圆的半径和，即可求出的最小值.
【详解】圆关于轴对称圆的圆心坐标，半径为1，圆的圆心坐标为，半径为3，
易知，当三点共线时，取得最小值，
的最小值为圆与圆的圆心距减去两个圆的半径和，
即：.
故选：A.
注意: 9至12题为多选题.
9. 已知直线：和直线：，下列说法正确的是（ ）
A. 始终过定点
B. 若，则或-3
C. 若，则或2
D. 当时，始终不过第三象限
【答案】ACD
【解析】
【分析】将直线化为可判断A；将或-3代入直线方程可判断B；根据可判断C；将直线化为，即可求解.
【详解】：过点，A正确；
当时，，重合，故B错误；
由，得或2，故C正确；
：始终过，斜率为负，不会过第三象限，故D正确.
故选：ACD
【点睛】本题考查了直线过定点、直线垂直求参数，考查了基本运算求解能力，属于基础题.
10. 为了更好地支持“中小型企业”的发展，某市决定对部分企业的税收进行适当的减免，现调查了当地的100家中小型企业年收入情况，并根据所得数据画出了样本的频率分布直方图，则下面结论正确的是
A. 样本在区间内的频数为18
B. 如果规定年收入在300万元以内企业才能享受减免税政策，估计有30%的当地中小型企业能享受到减免税政策
C. 样本的中位数小于350万元
D. 可估计当地的中小型企业年收入的平均数超过400万元（同一组中的数据用该组区间的中点值为代表
【答案】AB
【解析】
【分析】
由题意和图形及频率分布直方图的相关公式计算频率、中位数、平均数即可，
【详解】由图可得
样本在区间内的频数为，故A正确；
年收入在300万元以内的企业频率为，故B正确；
则中位数在之间，设为则，故C不正确；
年收入的平均数超过，故D不正确
故选：AB
【点睛】方法点睛：1.谨记频率分布直方图的相关公式：
(1)直方图中各小长方形的面积之和为1；
(2)直方图中纵轴表示：频率/组距，故每组样本的频率为组距乘以频率/组距，即矩形的面积；
(3)直方图中每组样本的频数为频率乘以总数.
2.频率分布直方图中数字特征的计算：
(1)最高的小长方形底边中点的横坐标即是众数；
(2)中位数左边和右边的小长方形的面积和是相等的；
(3)平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
11. 设，是两个平面，，是两条直线，下列命题正确的是（ ）
A. 如果，，那么.
B. 如果，，那么.
C. 如果，，，那么.
D. 如果内有两条相交直线与平行，那么.
【答案】ABD
【解析】
【分析】由立体几何知识对选项逐一判断
【详解】对于A，由线面垂直的性质知A正确
对于B，由面面平行的性质知B正确
对于C，若，，，可得或，而位置关系不确定，故C错误
对于D，由面面平行的判定定理知D正确
故选：ABD
12. 如图，在四棱锥中，底面为菱形，，侧面为正三角形，且平面平面，则下列说法正确的是（ ）
A. 在棱上存在点，使平面
B. 异面直线与所成的角为90°
C. 二面角的大小为45°
D 平面
【答案】ABC
【解析】
【分析】选项A，取的中点，利用三角形知识得垂直关系，再利用线面垂直的判定定理证明平面；选项B，利用平面，可得；选项C，先作出并证明所求的二面角为，再利用直角三角形知识求解；选项D，利用反证法，假设平面，再证明平面，得到，与与的夹角为矛盾来说明.
【详解】A选项：如图，取的中点，连接，
∵侧面为正三角形，，
又底面是菱形，，是等边三角形，
又为的中点，
又，，在平面内，且相交于点，
平面，故选项A正确；
B选项：由选项A知，平面，又平面，，
即异面直线与所成的角为90°，故选项B正确；
C选项：∵平面， ，
平面，，，
又平面平面，是二面角的平面角，
设，则，，
在直角中，，即，
故二面角的大小为，故选项C正确；
D选项：因为平面平面，，
所以平面，又平面，所以.
假设平面，则有，又，在平面内，且相交于点，
所以平面，又平面，所以，
而由题可知，与的夹角为，矛盾，故假设不成立，故选项D错误.
故选：ABC.
二、填空题（每小题5分，共20分）
13. 已知圆锥的高为，体积为，则以该圆锥的母线为半径的球的表面积为______________.
【答案】
【解析】
【分析】利用圆锥体积公式可求得圆锥底面半径，利用勾股定理可得母线长；根据球的表面积公式可求得结果.
【详解】设圆锥的底面半径为，母线长为，
圆锥体积，，，
以为半径的球的表面积.
故答案为：.
14. 直线的倾斜角的取值范围是______.
【答案】
【解析】
【分析】先求出直线的斜率取值范围，再根据斜率与倾斜角的关系，即可求出．
【详解】可化为：，所以，由于，结合函数在上的图象，可知．
故答案为：．
【点睛】本题主要考查斜率与倾斜角的关系的应用，以及直线的一般式化斜截式，属于基础题．
15. 已知水平放置的是按“斜二测画法”得到如下图所示的直观图，其中， ，则原的面积为______.
【答案】
【解析】
【分析】根据直观图画出原图，再根据三角形面积公式计算可得.
【详解】解：依题意得到直观图的原图如下：
且，
所以
故答案为：
【点睛】本题考查斜二测画法中原图和直观图面积之间的关系，属于基础题．
16. 如图,在四棱锥中,平面,底面是菱形,且,则异面直线与所成的角的余弦值为______,点到平面的距离等于______.
【答案】 ①. ②.
【解析】
【分析】
因为底面是菱形,可得,则异面直线与所成的角和与所成的角相等,即可求得异面直线与所成的角的余弦值.在底面从点向作垂线 ,求证垂直平面,即可求得答案.
【详解】根据题意画出其立体图形:如图
底面是菱形,

则异面直线与所成的角和直线与所成的角相等
平面,平面

又 ,底面是菱形

即
故:异面直线与所成的角的余弦值为:
在底面从点向作垂线
平面,平面

,
平面
故是到平面的距离

故答案为:,.
【点睛】本题考查了求异面直线的夹角和点到面距离,解题关键是掌握将求异面直线夹角转化为共面直线夹角的解法,考查了分析能力和推理能力,属于基础题.
三、解答题（共70分.注意：以一定的文字说明并规范答题）
17. 已知向量，.
（1）计算和；
（2）求.
【答案】（1）， ；（2）.
【解析】
【分析】
（1）利用空间向量的坐标运算可求得的坐标，利用向量的模长公式可求得的值；
（2）计算出，结合的取值范围可求得结果.
【详解】（1），；
（2），
，因此，.
【点睛】本题考查空间向量的坐标运算，同时也考查了利用空间向量的数量积计算向量的夹角，考查计算能力，属于基础题.
18. 已知三角形的三个顶点是，，．
（1）求边上的中线所在直线的方程；
（2）求边上的高所在直线的方程．
【答案】（1）；（2）．
【解析】
【分析】（1）先求出BC的中点坐标，再利用两点式求出直线的方程；
（2）先求出BC边上的高所在直线的斜率，再利用点斜式求出直线的方程.
【详解】（1）设线段的中点为．
因为，，
所以的中点，
所以边上的中线所在直线的方程为，
即．
（2）因为，，
所以边所在直线的斜率，
所以边上的高所在直线的斜率为，
所以边上的高所在直线的方程为，
即．
【点睛】本题主要考查直线方程的求法，属于基础题.
19. 某校从高一年级学生中随机抽取40名中学生，将他们的期中考试数学成绩(满分100分，成绩均为不低于40分的整数)分成六段：，，…，所得到如图所示的频率分布直图
（1）求图中实数的值；
（2）若该校高一年级共有640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；
（3）若从数学成绩在[40，50)与[90，100]两个分数段内的学生中随机选取两名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率.
【答案】（1）a=0.03；（2）544人；（3）.
【解析】
【分析】（1）根据图中所有小矩形的面积之和等于1求解.
（2）根据频率分布直方图，得到成绩不低于60分的频率，再根据该校高一年级共有学生640人求解.
（3）由频率分布直方图得到成绩在[40，50)和[90，100]分数段内的人数，先列举出从数学成绩在[40，50)与[90，100]两个分数段内的学生中随机选取两名学生的基本事件总数，再得到两名学生的数学成绩之差的绝对值不大于10”的基本事件数，代入古典概型概率求解.
【详解】（1）∵图中所有小矩形的面积之和等于1，
∴10×(0.005+0.01+0.02+a+0.025+0.01)=1，
解得a=0.03.
（2）根据频率分布直方图，成绩不低于60分的频率为1−10×(0.005+0.01)=0.85，
∵该校高一年级共有学生640人，
∴由样本估计总体的思想，可估计该校高一年级数学成绩不低于60分的人数约为640×0.85=544人.
（3）成绩在[40，50)分数段内的人数为40×0.05=2人，分别记为A，B，
成绩在[90，100]分数段内的人数为40×0.1=4人，分别记为C，D，E，F.
若从数学成绩在[40，50)与[90，100]两个分数段内的学生中随机选取两名学生，
则所有的基本事件有：(A，B)，(A，C)，(A，D)，(A，E)，(A，F)，(B，C)，(B，D)，(B，E)，(B，F)，(C，D)，(C，E)，
(C，F)，(D，E)，(D，F)，(E，F)共15种.
如果两名学生的数学成绩都在[40，50)分数段内或都在[90，100]分数段内，
那么这两名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40，50)分数段内，另一个成绩在[90，100]分数段内，
那么这两名学生数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M，
则事件M包含的基本事件有：(A，B)，(C，D)，(C，E)，(C，F)，(D，E)，(D，F)，(E，F)共7种.
∴所求概率为P(M)=.
【点睛】本题主要考查频率分布直方图的应用以及古典概型概率的求法，还考查了运算求解的能力，属于中档题.
20. 如图长方体中，，，点为的中点.
（1）求证：平面；
（2）求证：平面；
（3）求二面角的余弦值.
【答案】（1）见解析（2）见解析（3）
【解析】
【分析】（1）作辅助线，由中位线定理证明，再由线面平行的判定定理证明即可；
（2）连接，由勾股定理证明，，再结合线面垂直的判定定理证明即可；
（3）建立空间直角坐标系，利用向量法求面面角的余弦值即可.
【详解】（1）连接交与点，连接
四边形为正方形，点为的中点
又点为的中点，
平面，平面
平面
（2）连接
由勾股定理可知，
，则
同理可证，
平面
平面
（3）建立如下图所示的空间直角坐标系
显然平面的法向量即为平面的法向量，不妨设为
由（2）可知平面，即平面的法向量为
又二面角是钝角
二面角的余弦值为
【点睛】关键点睛：在第一问中，关键是利用中位线定理找到线线平行，再由定义证明线面平行；在第二问中，关键是利用勾股定理证明线线垂直，从而得出线面垂直；在第三问中，关键是建立坐标系，利用向量法求面面角的余弦值.
21. 已知圆.
（1）求过点M（2，1）的圆的切线方程；
（2）直线过点且被圆截得的弦长为2，求直线的方程；
（3）已知圆的圆心在直线y=1上，与y轴相切，且与圆相外切，求圆的标准方程.
【答案】（1）y=1；
（2）x+y-2=0；
（3）.
【解析】
【分析】(1)将圆的一般方程化为圆的标准方程，结合图形即可求出结果；
(2)根据题意可知直线过圆心，利用直线的两点式方程计算即可得出结果；
(3)设圆E的圆心E（a，1），根据题意可得圆E的半径为，结合圆与圆的位置关系和两点距离公式计算求出，进而得出圆的标准方程.
【小问1详解】
圆，
即，
其圆心为，半径为1.
因为点（2，1）在圆上，如图，
所以切线方程为y=1；
【小问2详解】
由题意得，圆的直径为2，
所以直线过圆心，
由直线的两点式方程，得，
即直线的方程为x+y-2=0；
【小问3详解】
因为圆E的圆心在直线y=1上，设圆E的圆心E（a，1），
由圆E与y轴相切，得R=a()
又圆E与圆相外切，所以，
由两点距离公式得，
所以，解得，
所以圆心，，
所以圆E的方程为.
22. 如图，在四棱锥中，底面是正方形，侧面底面，为侧棱上一点．
（1）求证：；
（2）若为中点，平面与侧棱于点，且，求四棱锥的体积．
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）利用面面垂直的性质定理可得出平面，再利用线面垂直的性质可得出；
（2）分析可知为的中点，平面，计算出梯形的面积，利用锥体的体积公式可求得四棱锥的体积．
【小问1详解】
证明：因为四边形为正方形，则，
因为侧面底面，平面平面，平面，
所以平面，又平面，所以.
【小问2详解】
解：因为，平面，平面，所以，平面，
因为平面，平面平面，所以，所以，
，则，所以，四边形是直角梯形，
又是中点，所以，，
所以，
由平面，平面，所以，从而，
正三角形中，是中点，，即，
，所以平面，
因为，所以.