2022-2023学年高二数学上学期期末常考题型重点突破02 用向量法证明平行与垂直

这是一份2022-2023学年高二数学上学期期末常考题型重点突破02 用向量法证明平行与垂直，文件包含常考题型02用向量法证明平行与垂直解析版docx、常考题型02用向量法证明平行与垂直原卷版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
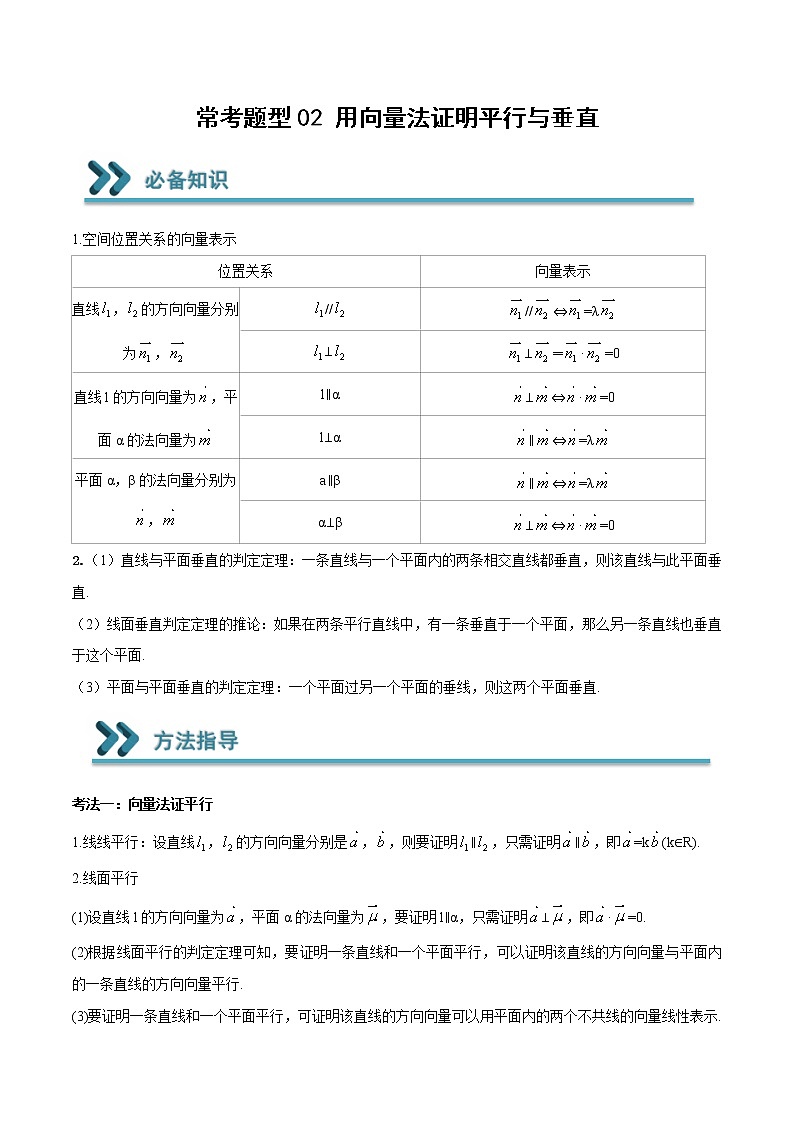
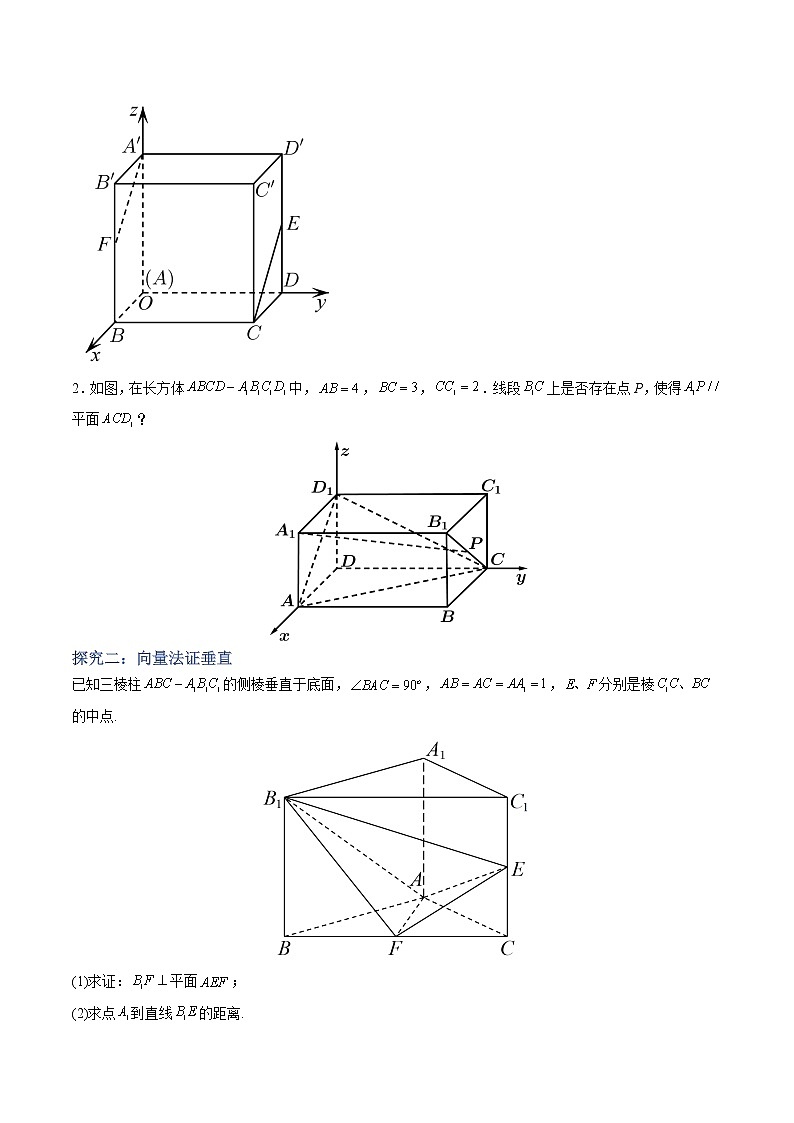
常考题型02 用向量法证明平行与垂直 1.空间位置关系的向量表示位置关系向量表示直线，的方向向量分别为，////⇔=λ⊥⊥═·=0直线l的方向向量为，平面α的法向量为l∥α⊥⇔·=0l⊥α∥⇔=λ平面α，β的法向量分别为，a∥β∥⇔=λα⊥β⊥⇔·=02.（1）直线与平面垂直的判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直.（2）线面垂直判定定理的推论：如果在两条平行直线中，有一条垂直于一个平面，那么另一条直线也垂直于这个平面.（3）平面与平面垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直.考法一：向量法证平行1.线线平行：设直线，的方向向量分别是，，则要证明∥，只需证明∥，即=k(k∈R).2.线面平行(1)设直线l的方向向量为，平面α的法向量为，要证明l∥α，只需证明⊥，即·=0.(2)根据线面平行的判定定理可知，要证明一条直线和一个平面平行，可以证明该直线的方向向量与平面内的一条直线的方向向量平行.(3)要证明一条直线和一个平面平行，可证明该直线的方向向量可以用平面内的两个不共线的向量线性表示.3.面面平行：证明两平面的法向量为共线向量.考法二：向量法证垂直1.线线垂直：设直线，的方向向量分别为，，则要证明⊥，只需证明⊥，即·=0.2.线面垂直：设直线l的方向向量是，平面α的法向量是，则要证明l⊥α，只需证明∥.3.面面垂直：要证明两个平面垂直，只需证明两个平面的法向量互相垂直.探究一：向量法证明直线、平面的平行如图，已知棱长为4的正方体ABCD﹣A1B1C1D1中，M，N，E，F分别是棱A1D1，A1B1，D1C1，B1C1的中点，求证：平面∥平面. 【变式练习】1．如图，在空间直角坐标系中有长方体，，，，点E，F分别是棱和的中点．求证：，并求它们的距离．2．如图，在长方体中，，，．线段上是否存在点P，使得平面？探究二：向量法证垂直已知三棱柱的侧棱垂直于底面，，，分别是棱的中点.(1)求证：平面；(2)求点到直线的距离.【变式练习】1．如图，在多面体中，四边形是梯形，四边形为矩形，面，，，．(1)求证：平面；(2)点为线段的中点，求证面．2．如图所示，在四棱锥中，平面，，在四边形中，，，，点在上，，与平面成的角.（1）平面；（2）平面平面.一、单选题1．在直三棱柱中，，，M，N分别是，的中点，则（    ）A．平面CMN B．平面CMNC． D．2．如图，下列正方体中，O为下底面的中心，M，N为正方体的顶点，P为所在棱的中点，则满足直线的是（    ）A． B．C． D．3．如图，已知正方体的棱长为2，M，N分别为，的中点．有下列结论：①三棱锥在平面上的正投影图为等腰三角形；②直线平面；③在棱BC上存在一点E，使得平面平面；④若F为棱AB的中点，且三棱锥的各顶点均在同一求面上，则该球的体积为．其中正确结论的个数是（    ）A．0 B．1 C．2 D．34．已知a，b是两条不同的直线，是三个不同的平面，则下列命题错误的是（    ）A．若，则B．若，则C．若，则D．若，则5．已知正方体的棱长为，则平面与平面的距离为（    ）A． B． C． D．6．如图，在正方体中，以为原点建立空间直角坐标系，为的中点，为的中点，则下列向量中，能作为平面的法向量的是（    ）．A．（1，，4） B．（，1，）C．（2，，1） D．（1，2，）7．如图已知正方体，点是对角线上的一点且，，则（    ）A．当时，平面 B．当时，平面C．当为直角三角形时， D．当的面积最小时，8．正方体的棱长为3，点E，F分别在棱上，且，，下列几个命题：①异面直线与垂直；②过点B，E，F的平面截正方体，截面为等腰梯形；③三棱锥的体积为④过点作平面，使得，则平面截正方体所得的截面面积为．其中真命题的序号为（    ）A．①④ B．①③④ C．①②③ D．①②③④二、多选题9．如图，正方体的棱长为2，M为棱的中点，N为棱上的点，且，则（    ）A．当时，平面B．当时，点C到平面BDN的距离为C．当时，三棱锥外接球的表面积为D．对任意，直线与都是异面直线10．如图，在边长为的正方体中，点在线段上运动，则下列结论正确的是（    ）A．B．的最小值为C．异面直线与的距离是定值D．11．以下命题正确的是（    ）A．若是平面的一个法向量，直线上有不同的两点A，，则的充要条件是B．已知A，，三点不共线，对于空间任意一点，若，则，A，，四点共面C．已知，，若与垂直，则D．已知的顶点坐标分别为，，，则边上的高的长为12．如图，直三棱柱中，，，D，E，M分别为，，的中点，点N是棱AC上一动点，则(    )A． B．存在点N，平面C．∥平面 D．存在点N，三、填空题13．正方体ABCD﹣A1B1C1D1的棱长为1，点M在线段CC1上，且．点P在平面A1B1C1D1上，且AP⊥平面MBD1，则线段AP的长为________．14．如图，在正方体中，点为线段上的动点，分别为棱的中点，若平面，则_______．15．在平行六面体中，面面，底面为矩形，，，面为菱形，，是的中点，为的中点，问_______时，面面．16．如图，在长方体中，，点为线段上的动点(包含线段端点)，则下列结论正确的__________．①当时，∥平面；②当时，平面；③的最大值为；④的最小值为.四、解答题17．已知平行六面体的所有棱长均为1，．用向量解决下面的问题(1)求的长；(2)求证：平面．18．如图，在直三棱柱-中，3，=4，5，(1)求证；(2)在上是否存在点，使得并说明理由19．如图，在四棱锥中，底面ABCD，，，，，E为PC上一点，且．(1)求证：平面PBC；(2)求证：平面BDE．20．在三棱锥中，平面平面，，，为线段的中点，点，，分别在线段，，上，且，.若，以为坐标原点建立如图所示的空间直角坐标系.(1)求点的坐标；(2)用向量法证明平面平面.