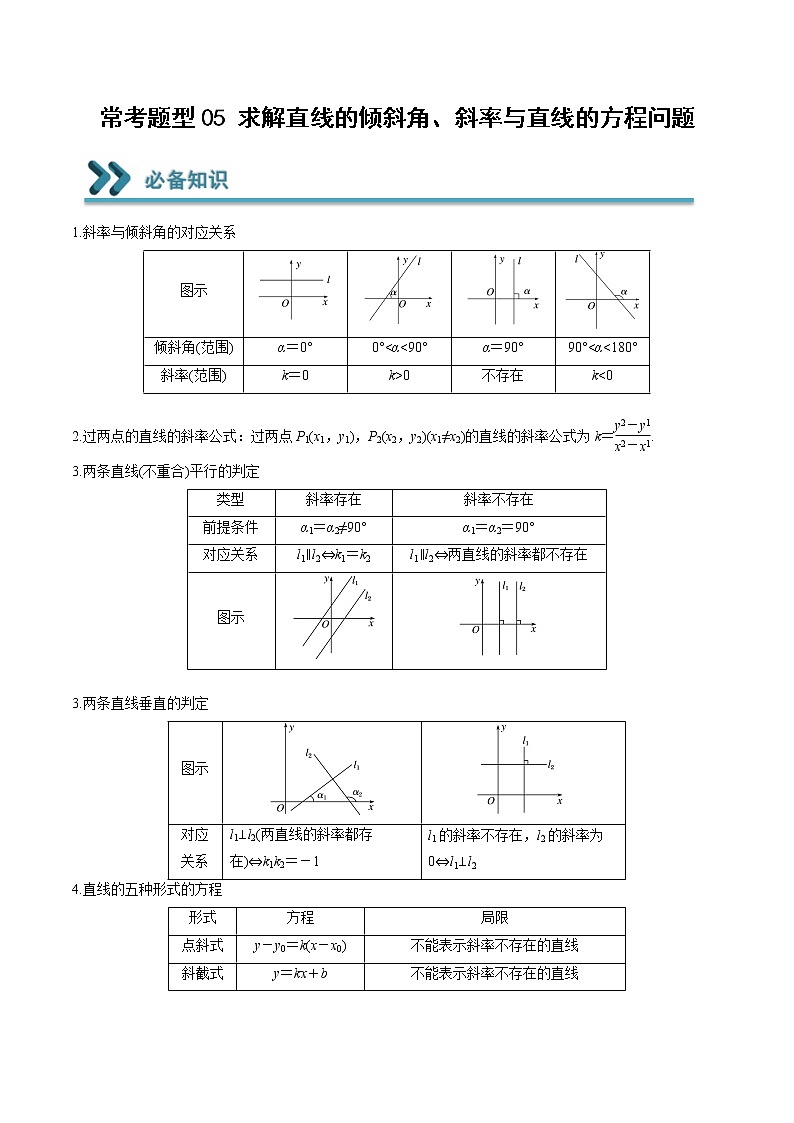
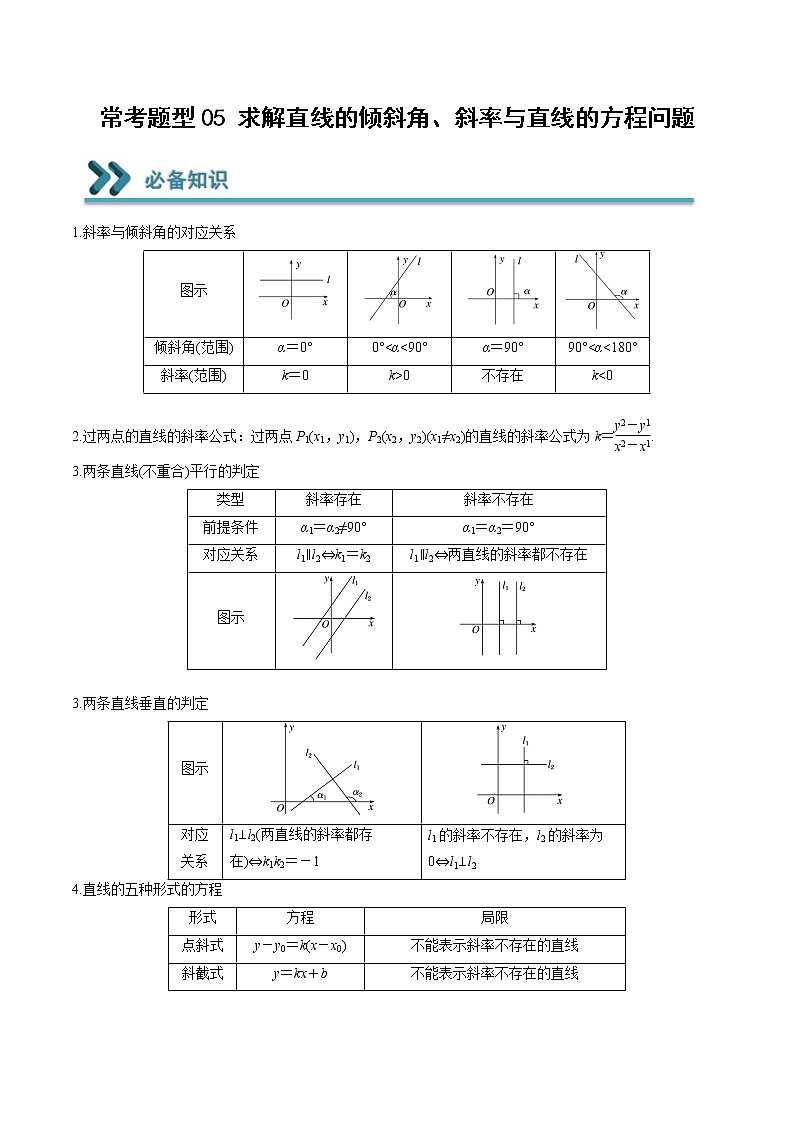
2022-2023学年高二数学上学期期末常考题型重点突破05 求解直线的倾斜角、斜率与直线的方程问题

这是一份2022-2023学年高二数学上学期期末常考题型重点突破05 求解直线的倾斜角、斜率与直线的方程问题，文件包含常考题型05求解直线的倾斜角斜率与直线的方程问题解析版docx、常考题型05求解直线的倾斜角斜率与直线的方程问题原卷版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
常考题型05 求解直线的倾斜角、斜率与直线的方程问题 1.斜率与倾斜角的对应关系图示倾斜角(范围)α＝0°0°<α<90°α＝90°90°<α<180°斜率(范围)k＝0k>0不存在k<0 2.过两点的直线的斜率公式：过两点P1(x1，y1)，P2(x2，y2)(x1≠x2)的直线的斜率公式为k＝.3.两条直线(不重合)平行的判定类型斜率存在斜率不存在前提条件α1＝α2≠90°α1＝α2＝90°对应关系l1∥l2⇔k1＝k2l1∥l2⇔两直线的斜率都不存在图示 3.两条直线垂直的判定图示对应关系l1⊥l2(两直线的斜率都存在)⇔k1k2＝－1l1的斜率不存在，l2的斜率为0⇔l1⊥l24.直线的五种形式的方程形式方程局限点斜式y－y0＝k(x－x0)不能表示斜率不存在的直线斜截式y＝kx＋b不能表示斜率不存在的直线两点式＝x1≠x2，y1≠y2截距式＋＝1不能表示与坐标轴平行及过原点的直线一般式Ax＋By＋C＝0无考法一：直线的倾斜角与斜率1.在已知斜率表达式的情况下，研究倾斜角的范围，应首先求出斜率的取值范围.2.解决三点共线问题，若已知三个点中的两个点的坐标，可以先通过这两个已知点求出直线方程，然后将第三个点代入求解；也可利用斜率相等或向量共线求解.3.在解决与含参数的直线方程有关的直线相交问题时，首先要考虑该直线是否过定点.考法二：求直线的方程1.直接法：根据已知条件，选择适当的直线方程形式，直接写出直线方程.2.待定系数法：(1)设:设出所求直线方程的某种形式.(2)列:由条件列出所求参数的方程(组).(3)解:解这个方程(组)求出参数.(4)代:把参数的值代入所设直线方程.考法三：利用直线的斜率判断两条直线的位置关系1.判断平行先确定题中两条不重合的直线的斜率是否存在，若斜率均不存在，则两直线平行；若只有一条直线斜率存在，则两条直线不平行；若两条直线的斜率均存在，则利用斜率公式求出斜率，再利用两条直线平行的条件判断它们是否平行.（1）判断两条直线是否平行，应首先看两条直线的斜率是否存在，即先看两点的横坐标是否相等，对于横坐标相等这种特殊情况，应特殊判断.（2）在证明两条直线平行时，要区分平行与重合，必须强调不共线才能确定平行.因为斜率相等也可以推出两条直线重合.2.判断垂直当两直线的斜率都存在时，求出斜率，利用垂直的条件（两直线的斜率之积等于—1)判断.当一条直线的斜率不存在时，看另一条直线的斜率是否为0，若为0，则垂直；否则，不垂直。利用斜率公式来判定两直线垂直的步骤如下：一看：看所给两点的横坐标是否相等.若相等，则直线的斜率不存在，此时只需看另一条直线的两点的纵坐标是否相等，若相等，则垂直.若所给两点的横坐标不相等，则进行第二步.二代：将点的坐标代入斜率公式.三求：计算斜率的值，进行判断.当点的坐标中含有参数时，应用斜率公式前要对参数进行讨论.考法四：利用直线的方程判断两直线的位置关系1.根据斜截式方程判断已知直线：y=x+与直线：y=x+，①若∥，则=，此时两直线与y轴的交点不同，即≠；反之当=，且≠时，∥.所以有∥⇌=，且≠.②若⊥，则·=-1；反之当·=-1时，⊥.所以有⊥⇌·=-1.2.根据一般式方程判断由一般式方程判断两直线位置关系的方法直线方程：x+y+=0(+≠0)；：x+y+=0(+≠0)与垂直的条件+=0与平行的条件(≠0)与相交的条件(≠0)与重合的条件(≠0)探究一：直线的倾斜角与斜率已知直线经过两点，则直线的倾斜角的取值范围为（    ）A． B． C． D．【变式练习】1．已知点，，若，则直线的倾斜角的取值范围为（    ）A．B．或C．或D．或2．已知，两点，若直线与线段恒有交点，则的取值范围是（    ）A． B．C． D．探究二：求直线的方程直线l过点（1，2），且纵截距为横截距的两倍，则直线l的方程是___________.【变式练习】1．直线过点，且与直线平行，则直线的一般式方程为______．2．直线l经过点，且与两坐标轴围成一个等腰直角三角形，则l的点斜式方程为______．探究三：利用直线的斜率判断两条直线的位置关系是直线：与直线：平行的（    ）条件A．充分不必要  B．必要不充分C．充要  D．既不充分也不必要【变式练习】1．已知直线，，若，则实数m的值是（    ）A． B．2 C．或2 D．或2．某菱形的一组对边所在的直线方程分别为和，另一组对边所在的直线方程分别为和，则（    ）A． B． C．2 D．4探究四：利用直线的方程判断两直线的位置关系已知直线，，，则“”的必要不充分条件是（    ）A． B．C．或 D．【变式练习】1．已知两条直线：，：，则下列说法正确的是（    ）A．与一定相交 B．与一定平行C．与一定相交或平行 D．以上均不对2．过点且与直线平行的直线方程是（    ）A． B． C． D．一、单选题1．直线的斜率的取值范围为（    ）A． B． C． D．2．已知点，，，过的直线（不垂直于轴）与线段相交，则直线斜率的取值范围是（    ）A． B．C． D．3．直线的倾斜角的取值范围是（    ）A． B．C． D．4．已知直线y＝mx﹣2与直线x+ny＝0平行，则m，n的关系为（    ）A．mn＝1 B．mn+1＝0 C．m﹣n＝0 D．m﹣n+1＝05．某直线l过点，且在x轴上的截距是在y轴上截距的2倍，则该直线的斜率是（    ）A． B． C．或 D．或6．设，过定点的动直线和过定点的动直线交于点，则的最大值是（    ）A．4 B．10 C．5 D．7．已知直线l与直线：，：的夹角相等，且直线l过点，则直线l的方程为（    ）A． B．C． D．或8．已知点，又、分别为过点的直线的法向量和斜率，有下列直线方程：①；②；③（，且）．其中能表示所有过点的直线方程的个数是（    ）A．0 B．1 C．2 D．3二、多选题9．已知点，，．若为直角三角形，则可能有（　　）A． B．C． D．10．下列说法中，正确的是（ 　  ）A．直线在轴上的截距是3B．直线的倾斜角为C．三点共线D．直线与垂直11．已知直线，则（    ）A．恒过点 B．若，则C．若，则 D．当时，不经过第三象限12．已知直线和直线，则（       ）A．始终过定点 B．若在x轴和y轴上的截距相等，则C．若，则或2 D．若，则或三、填空题13．已知两条直线、，其中，当这两条直线的夹角在内变化时，a的取值范围为______．14．已知，，，，若直线直线，则_____．15．已知直线与两坐标轴围成的三角形的面积不小于5，则k的取值范围为______．16．已知直线与直线互相垂直，则实数的值为__________.四、解答题17．已知点、．(1)当时，直线MN的倾斜角为何值？(2)当m取何值时，直线MN的倾斜角为锐角、直角、钝角？18．（1）求过点且平行于直线的直线的方程；（2）求过点且垂直于直线的直线的方程．19．已知直线经过定点P．(1)证明：无论k取何值，直线l始终过第二象限；(2)若直线l交x轴负半轴于点A，交y轴正半轴于点B，当取最小值时，求直线l的方程．20．在平面直角坐标系中，已知菱形的顶点和所在直线的方程为.(1)求对角线所在直线方程；(2)已知直线过点，与直线的夹角为，求直线的方程.（以上所求方程都以直线的一般式方程作答）