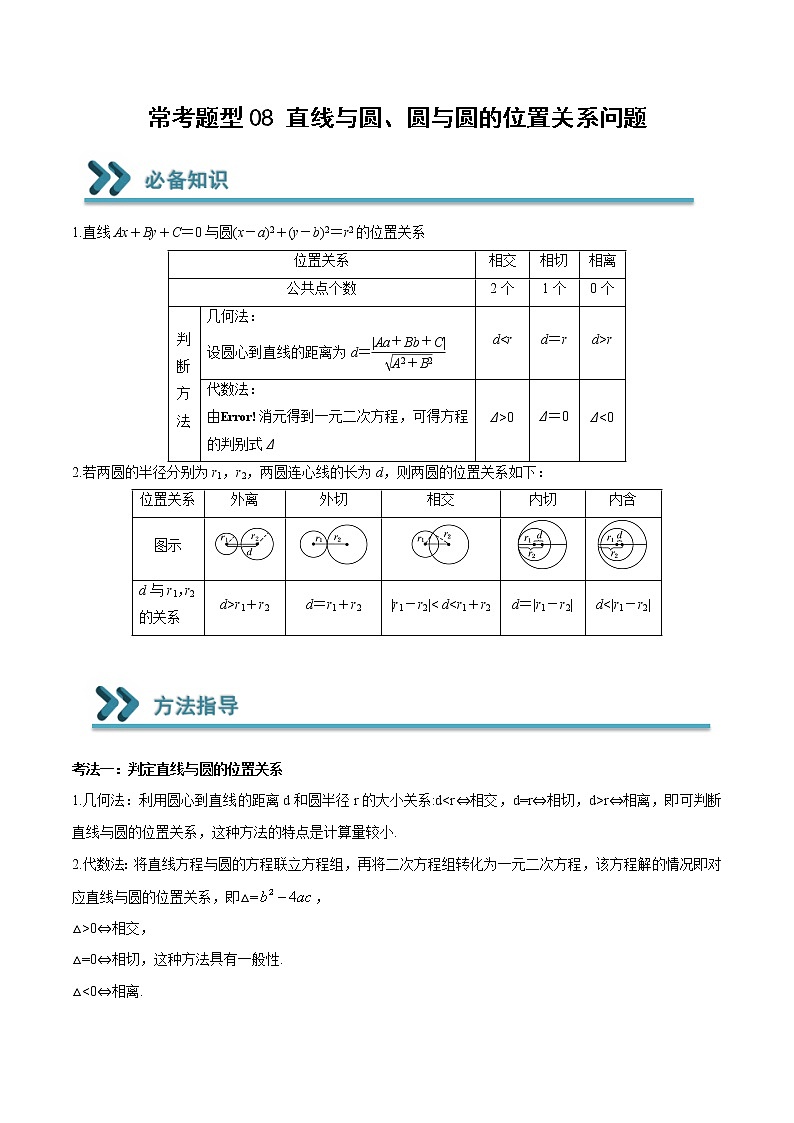
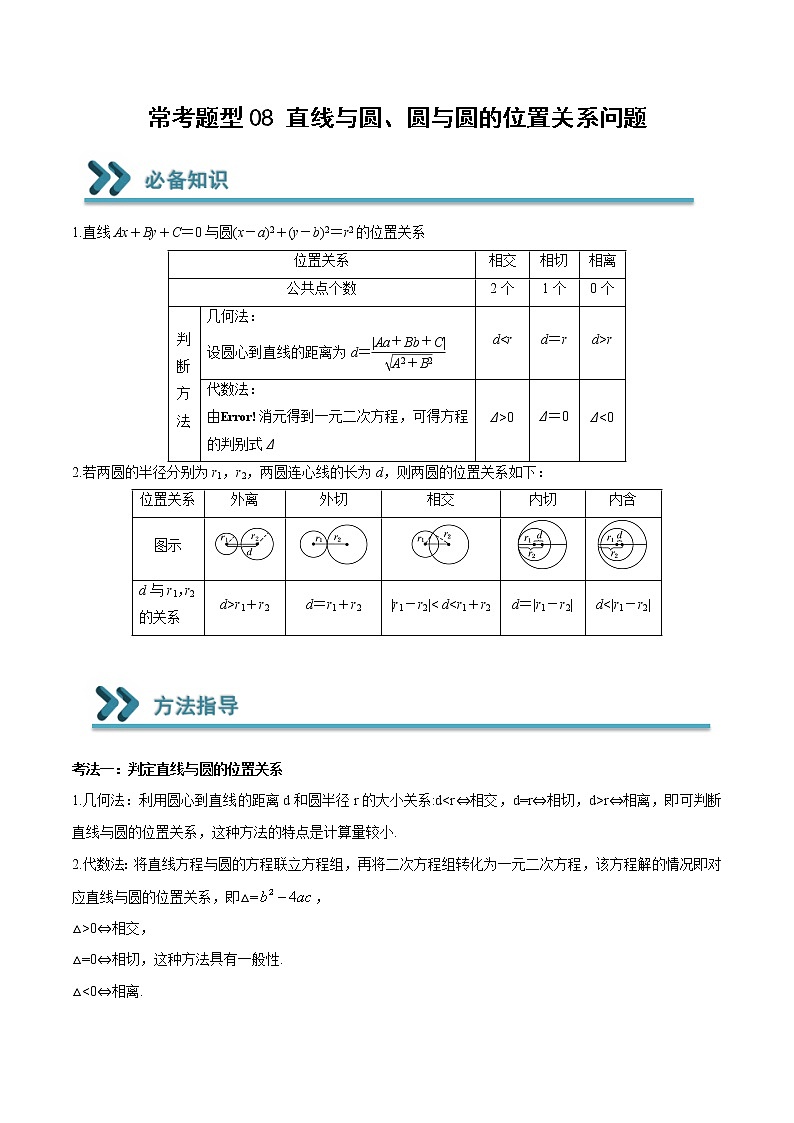
2022-2023学年高二数学上学期期末常考题型重点突破08 直线与圆、圆与圆的位置关系问题

这是一份2022-2023学年高二数学上学期期末常考题型重点突破08 直线与圆、圆与圆的位置关系问题，文件包含常考题型08直线与圆圆与圆的位置关系问题解析版docx、常考题型08直线与圆圆与圆的位置关系问题原卷版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
常考题型08 直线与圆、圆与圆的位置关系问题 1.直线Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2的位置关系位置关系相交相切相离公共点个数2个1个0个判断方法几何法：设圆心到直线的距离为d＝d<rd＝rd>r代数法：由消元得到一元二次方程，可得方程的判别式ΔΔ>0Δ＝0Δ<02.若两圆的半径分别为r1，r2，两圆连心线的长为d，则两圆的位置关系如下：位置关系外离外切相交内切内含图示d与r1，r2的关系d>r1＋r2d＝r1＋r2|r1－r2|< d<r1＋r2d＝|r1－r2|d<|r1－r2| 考法一：判定直线与圆的位置关系1.几何法：利用圆心到直线的距离d和圆半径r的大小关系:d<r⇔相交，d=r⇔相切，d>r⇔相离，即可判断直线与圆的位置关系，这种方法的特点是计算量较小.2.代数法：将直线方程与圆的方程联立方程组，再将二次方程组转化为一元二次方程，该方程解的情况即对应直线与圆的位置关系，即△=，△>0⇔相交，△=0⇔相切，这种方法具有一般性.△<0⇔相离.考法二：求圆的切线方程1.求过圆上一点(，)的圆的切线方程的方法先求切点与圆心连线的斜率k，若k不存在，则结合图形可直接写出切线方程为y=；若k=0，则结合图形可直接写出切线方程为x=；若k存在且k≠0，则由垂直关系知切线的斜率为一，由点斜式可写出切线方程.2.求过圆外一点(，)的圆的切线方程的两种方法(1)几何法当斜率存在时，设为k，则切线方程为y-=k(x-)，即kx-y+-k=0.由圆心到直线的距离等于半径，即可求出k的值，进而写出切线方程.(2)代数法当斜率存在时，设为k，则切线方程为y-=k(x-)，即y=kx-k+，代入圆的方程，得到一个关于x的一元二次方程，由△=0，求得k，进而写出切线方程.考法三：圆的弦长问题1.几何法：设直线l被圆C截得的弦为AB，圆的半径为r，圆心到直线l的距离为d，则有关系式:|AB|=2。2.代数法：若斜率为k的直线l与圆C相交于A(，)，B(，)两点，则|AB|==●=●(其中k≠0).特别地，当k=0时，|AB|=；当斜率不存在时，|AB|=。考法四：圆与圆的位置关系1.两圆位置关系的判断方法：多用圆心距与半径和或差的关系判断，一般不采用代数法.2.两相交圆的公共弦所在直线方程及公共弦长的求法若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差得到，即若圆：与圆：相交，则两圆公共弦所在直线的方程为。探究一：判定直线与圆的位置关系对于任意实数，圆与直线的位置关系是（   ）A．相交 B．相切C．相离 D．与的取值有关【变式练习】1．在平面直角坐标系xOy中，已知直线l：，当变化时，动直线始终没有经过点P，定点Q的坐标为，则的取值范围为（    ）A． B． C． D．2．圆与直线的位置关系为（    ）A．相切 B．相离 C．相交 D．无法确定探究二：求圆的切线方程设圆与y轴的正半轴交于点A，过点A作圆O的切线为l，对于切线l上的点B和圆O上的点C，下列命题中正确的是（    ）A．若，则点B的坐标为 B．若，则C．若，则 D．若，则【变式练习】1．过直线上任一点P作圆O：的两条切线，切点分别为A，B，若直线AB与圆M：恒有公共点，则t的取值范围是（       ）A． B． C． D．2．从原点O引圆的切线，当m变化时，切点P的轨迹方程是（    ）A． B．C． D．探究三：圆的弦长问题已知二次函数交轴于两点(不重合)，交轴于点. 圆过三点.下列说法正确的是（    ）① 圆心在直线上；② 的取值范围是；③ 圆半径的最小值为；④ 存在定点，使得圆恒过点.A．①② B．③④ C．②③ D．①④【变式练习】1．已知直线与圆交于两点，过分别作的垂线与轴交于两点，则当最小时，（    ）A．4 B． C．8 D．2．已知圆：，直线过点与圆交于A，B两点，若点为线段的中点，则直线的方程为（    ）A． B．C． D．探究四：圆与圆的位置关系已知直线与圆交于两个不同点，则当弦最短时，圆与圆的位置关系是（    ）A．内切 B．相离 C．外切 D．相交【变式练习】1．已知直线，过直线l上的动点P作圆的两条切线，切点分别为A，B，则点到直线的距离最大值为（    ）A． B． C． D．2．若圆与圆的公共弦的长为1，则下列结论正确的有（    ）A．B．C．中点的轨迹方程为D．中点的轨迹方程为一、单选题1．关于的方程有两个不相等的实数根，则实数的取值范围为（    ）A． B． C． D．2．设圆的圆心为C，直线l过点，且与圆C交于A，B两点，若，则直线l的方程为（    ）A． B．或C．x=0 D．x=0或3．过点作圆C：的切线l，直线m：与切线l平行，则切线l与直线m间的距离为（    ）A．4 B．2 C． D．4．过点的直线与圆相切，则直线的方程为（    ）A．或 B．或C．或 D．或5．已知圆：，直线：，直线被圆截得的弦长最短时，的方程为（    ）A． B． C． D．6．圆与圆至少有三条公切线，则m的取值范围是（    ）A． B．C． D．7．过点作圆的两条切线，设切点分别为、，则直线的方程为（    ）A． B． C． D．8．圆与的公共弦长为（    ）A． B． C． D．二、多选题9．已知圆与直线，下列选项正确的是（    ）A．圆的圆心坐标为 B．直线过定点C．直线与圆相交且所截最短弦长为 D．直线与圆可以相切10．过点的直线与圆交于A，B两点，线段MN是圆C的一条动弦，且，则（    ）A．面积的最大值为 B．面积的最大值为C．的最小值为 D．的最小值为11．已知圆与圆，则下列说法正确的是（    ）A．若圆与轴相切，则B．若，则圆C1与圆C2相离C．若圆C1与圆C2有公共弦，则公共弦所在的直线方程为D．直线与圆C1始终有两个交点12．已知圆和圆的交点为、，则（    ）A．两圆的圆心距B．圆上存点，圆上存在点，使得C．圆上存在两点和使得D．圆上的点到直线的最大距离为三、填空题13．圆与直线的位置关系为__________.14．过圆外一点引圆的两条切线，则经过两切点的直线方程是________．15．平面直角坐标系xOy中，已知圆C1：(x－4)2＋(y－8)2＝1，圆C2：(x－6)2＋(y＋6)2＝9，若圆心在x轴上的圆C同时平分圆C1和圆C2的圆周，则圆C的方程是________．16．已知的圆心在轴上，半径为1，且过点，，则与的公共弦长为___________.四、解答题17．已知圆M：，Q是x轴上的动点，、分别与圆相切于两点.(1)若，求切线方程；(2)求四边形面积的最小值；18．已知圆，Q是x轴上的动点，QA、QB分别与圆M相切于A、B两点．(1)若，求切线方程；(2)求四边形QAMB面积的最小值；(3)若，求直线MQ的方程．19．已知圆，圆.(1)求圆与圆的公共弦长；(2)求过两圆的交点且圆心在直线上的圆的方程.20．已知圆与y轴相切于点，圆心在经过点与点的直线l上．(1)求圆的方程；(2)若圆与圆相交于M，N两点，求两圆的公共弦长．