河南省驻马店市平舆县2022-2023学年九年级上学期期中数学试卷+

这是一份河南省驻马店市平舆县2022-2023学年九年级上学期期中数学试卷+，共12页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
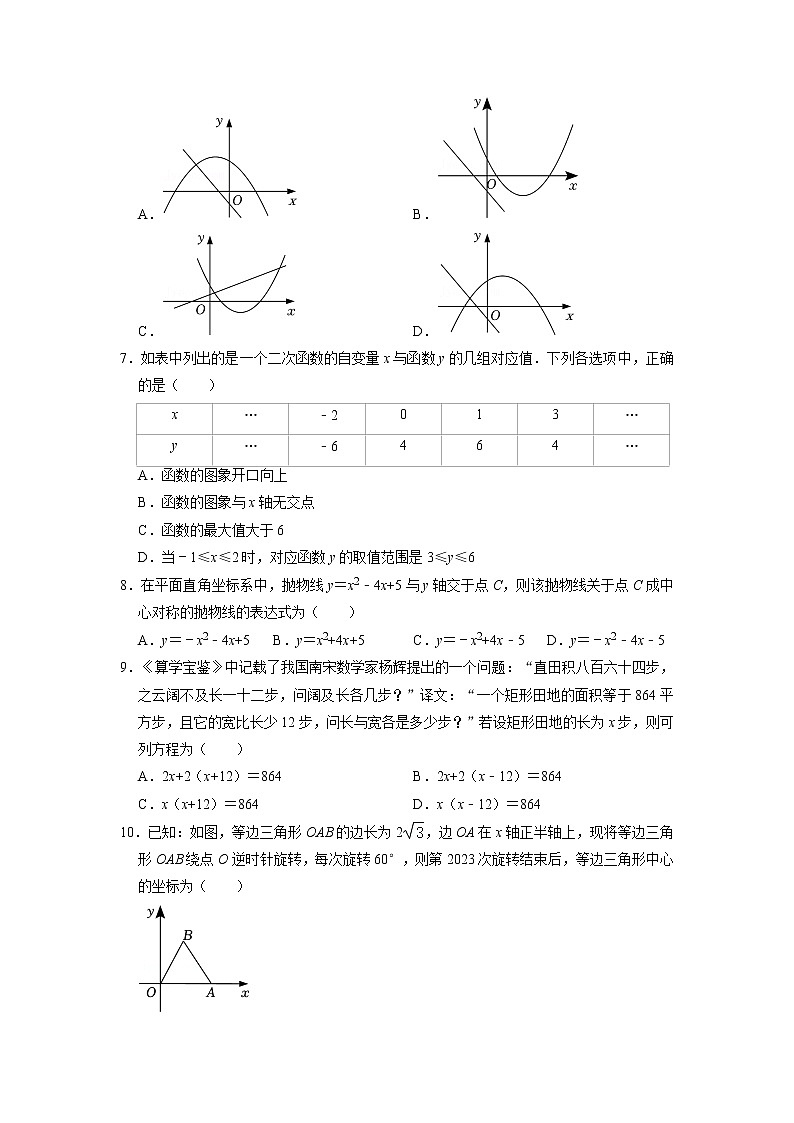
河南省驻马店市平舆县2022-2023学年九年级（上）期中数学试卷一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案填涂在答题卡上.1．下列图形中，既是轴对称图形又是中心对称图形的是（　　）A． B． C． D．2．若方程ax2+bx+c＝x2（a，b，c为常数）是关于x的一元二次方程，则（　　）A．a＝0 B．a≠0 C．a≠1 D．b≠03．如图，AB为⊙O直径，点C，D在⊙O上，＝，AD与CO交于点E，∠DAB＝30°，若，则CE的长为（　　）A．1 B． C． D．4．将抛物线y＝x2﹣2x的图象向左平移2个单位，再向下平移1个单位得到将抛物线必经过（　　）A．（1，2） B．（﹣1，2） C．（1，﹣2） D．（0，﹣2）5．关于x的一元二次方程（a﹣1）x2﹣2x﹣1＝0有两个实数根，则实数a的取值范围是（　　）A．a≥0 B．a≥0且a≠1 C．a≤0 D．a＞0且a≠16．在同一直角坐标系中，函数y＝ax+a和函数y＝ax2+x+2（a是常数，且a≠0）的图象可能是（　　）A． B． C． D．7．如表中列出的是一个二次函数的自变量x与函数y的几组对应值．下列各选项中，正确的是（　　）x…﹣2 013…y…﹣6 464…A．函数的图象开口向上 B．函数的图象与x轴无交点 C．函数的最大值大于6 D．当﹣1≤x≤2时，对应函数y的取值范围是3≤y≤68．在平面直角坐标系中，抛物线y＝x2﹣4x+5与y轴交于点C，则该抛物线关于点C成中心对称的抛物线的表达式为（　　）A．y＝﹣x2﹣4x+5 B．y＝x2+4x+5 C．y＝﹣x2+4x﹣5 D．y＝﹣x2﹣4x﹣59．《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔不及长一十二步，问阔及长各几步？”译文：“一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽各是多少步？”若设矩形田地的长为x步，则可列方程为（　　）A．2x+2（x+12）＝864 B．2x+2（x﹣12）＝864 C．x（x+12）＝864 D．x（x﹣12）＝86410．已知：如图，等边三角形OAB的边长为2，边OA在x轴正半轴上，现将等边三角形OAB绕点O逆时针旋转，每次旋转60°，则第2023次旋转结束后，等边三角形中心的坐标为（　　）A．（0，2） B．（0，﹣1） C．（﹣，﹣1） D．（﹣，1）二、填空题：（每小题3分，共15分）11．方程x（x﹣3）＝5（x﹣3）的解是 　   　．12．已知点A（x1，y1），B（x2，y2）在二次函数y＝（x﹣3）2﹣2的图象上，若x1＜x2＜3，则y1　   　y2（填“＞”、“＜”或“＝”）．13．如图，△ODC是由△OAB绕点O顺时针旋转30°后得到的图形，若点D恰好落在AB上，则∠ADO的度数为 　   　．14．如果关于x的一元二次方程x2﹣3x﹣7＝0的两根分别为m、n，那么m2﹣4m﹣n＝　   　．15．二次函数y＝ax2+bx+c（a≠0）的图象如图，则下列结论：（1）abc＞0；（2）b2﹣4ac＜0；（3）a﹣b+c＞0；（4）2a+b＝0；（5）若方程ax2+bx+c（a≠0）的两个根为x1，x2，则x1+x2＝2；（6）当x＞0时，y随x的增大而减小．其中正确的结论是：　   　．三、解答题：（本大题8个小题，共75分）16．（8分）解方程：（1）（2x﹣1）2＝16；（2）2x2+8x﹣1＝0．17．（9分）如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上．（1）画出将△ABC向左平移5个单位长度，再向上平移1个单位长度得到的图形△A1B1C1，则点A1的坐标为A1（ 　   　，　   　）；（2）画出△ABC关于点O成中心对称的图形△A2B2C2，则点A2的坐标为A2（ 　   　，　   　）；（3）画出将△ABC绕点B顺时针旋转90°得到的图形△A3B3C3，则点A3的坐标为A3（ 　   　，　   　）．18．（9分）已知关于x的一元二次方程x2﹣6x+m+4＝0有两个实数根x1，x2．（1）求m的取值范围．（2）若x1，x2满足3x1＝x2+2，求m的值．19．（9分）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面（要求用尺规作图，保留作图痕迹，不写作法）；（2）若这个输水管道有水部分的水面宽AB＝16cm，水面最深地方的高度（即的中点到弦AB的距离）为4cm，求这个圆形截面所在圆的半径．20．（9分）某小区有一个半径为3m的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心1m处达到最大高度为3m，且各个方向喷出的水柱恰好在喷水池中心的装饰物处汇合，以水平方向为x轴，喷水池中心为原点建立如图所示的平面直角坐标系．（1）求水柱所在抛物线对应的函数关系式；（2）王师傅在喷水池维修设备期间，喷水池意外喷水，如果他站在与池中心水平距离为2m处，通过计算说明身高1.8m的王师傅是否被淋湿？21．（10分）为防控新冠疫情，减少交叉感染，某超市在线上销售优质农产品，该超市于今年一月底收购一批农产品，二月份销售256盒，三、四月该商品十分畅销，销售量持续走高，在售价不变的基础上，四月份的销售量达到400盒．若农产品每盒进价25元，原售价为每盒40元．（1）求三、四这两个月销售量的月平均增长率；（2）该超市五月份降价促销，经调查发现，若该农产品每盒降价1元，销售量可增加5盒，当农产品每盒降价多少元时，这种农产品在五月份可获利4250元？22．（11分）在平面直角坐标系xOy中，直线y＝4x+4与x轴，y轴分别交于点A，B，抛物线y＝ax2+bx﹣3a经过点A，将点B向右平移5个单位长度，得到点C．（1）求点C的坐标；（2）求抛物线的对称轴；（3）若抛物线与线段BC恰有一个公共点，结合函数图象，求a的取值范围．23．（10分）阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形片△ABC和△C1DE叠放在一起（C与C1重合）的图形．操作与证明：（1）操作：固定△ABC，将△C1DE绕点C按顺时针方向旋转30°，连接AD，BE（如图2），线段BE与AD之间具有的大小关系为　   　．（2）操作：若将图1中的△C1DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE（如图3），线段BE与AD之间具有怎样的大小关系？证明你的结论．猜想与发现：（3）根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大？是多少？当α为多少度时，线段AD的长度最小？是多少？
河南省驻马店市平舆县2022-2023学年九年级（上）期中数学试卷参考答案一、选择题（每小题3分，共30分）下列各小题均有四个答案，其中只有一个是正确的，将正确答案填涂在答题卡上.1．D    2．C   3．C   4．A   5．B   6．D   7．D     8．A9．D    10．A二、填空题：（每小题3分，共15分）11．答案为：x1＝3，x2＝5．12．答案为：＞．13．答案为：75°．14．答案为：4．15．答案为：（3）（4）（5）．三、解答题：（本大题8个小题，共75分）16．（8分）解：（1）（2x﹣1）2＝16，开方得：2x﹣1＝4或2x﹣1＝﹣4，解得：x1＝2.5，x2＝﹣1.5；（2）2x2+8x﹣1＝0，整理得：x2+4x＝，配方得：x2+4x+4＝，即（x+2）2＝，开方得：x+2＝±，解得：x1＝﹣2+，x2＝﹣2﹣．17．（9分）解：（1）如图，△A1B1C1即为所求，点A1的坐标为（﹣3，6）．故答案为：﹣3，6．（2）如图，△A2B2C2即为所求，点A2的坐标为（﹣2，﹣5）．故答案为：﹣2，﹣5．（3）如图，△A3B3C3即为所求，点A3的坐标为（5，0）．故答案为：5，0．18．（9分）解：（1）∵关于x的一元二次方程x2﹣6x+m+4＝0有两个实数根x1，x2，∴Δ＝（﹣6）2﹣4（m+4）＝20﹣4m≥0，解得：m≤5，∴m的取值范围为m≤5；（2）∵关于x的一元二次方程x2﹣6x+m+4＝0有两个实数根x1，x2，∴x1+x2＝6①，x1•x2＝m+4②．∵3x1＝x2+2③，∴联立①③解得：x1＝2，x2＝4，∴8＝m+4，m＝4；∴m的值为4．19．（9分）解：（1）如图所示，⊙O为所求作的圆形截面． （2）连接OA，则AD＝AB＝8cm，点C为的中点，进而，CD＝4cm．设这个圆形截面所在圆的半径为r cm，则OD＝（r﹣4）cm．在Rt△ADO中，有82+（r﹣4）2＝r2，解得r＝10．即这个圆形截面所在圆的半径为10cm．20．（9分）解：（1）由题意知抛物线顶点坐标为（1，3），设抛物线解析式为y＝a（x﹣1）2+3，将点C（3，0）代入，得：4a+3＝0，解得a＝﹣，∴抛物线解析式为y＝﹣（x﹣1）2+3；（2）当x＝2时，y＝﹣（x﹣1）2+3＝﹣×（2﹣1）2+3＝＞1.8，∴身高1.8m的王师傅不会被淋湿．21．（10分）解：（1）设三、四这两个月销售量的月平均增长率为x，依题意得：256（1+x）2＝400，解得：x1＝0.25，x2＝﹣2.25（不符合题意，舍去）．答：三、四这两个月销售量的月平均增长率为25%．（2）设农产品每盒降价y元，则每盒的销售利润为（40﹣y﹣25）元，五月份可售出（400+5y）盒，依题意得：（40﹣y﹣25）（400+5y）＝4250，整理得：y2+65y﹣350＝0，解得：y1＝5，y2＝﹣70（不符合题意，舍去）．答：当农产品每盒降价5元时，这种农产品在五月份可获利4250元．22．（11分）解：（1）与y轴交点：令x＝0代入直线y＝4x+4得y＝4，∴B（0，4），∵点B向右平移5个单位长度，得到点C，∴C（5，4）；（2）与x轴交点：令y＝0代入直线y＝4x+4得x＝﹣1，∴A（﹣1，0），将点A（﹣1，0）代入抛物线y＝ax2+bx﹣3a中得0＝a﹣b﹣3a，即b＝﹣2a，∴抛物线的对称轴x＝﹣＝﹣＝1；（3）∵抛物线y＝ax2+bx﹣3a经过点A（﹣1，0）且对称轴x＝1，由抛物线的对称性可知抛物线也一定过A的对称点（3，0），①a＞0时，如图1，将x＝0代入抛物线得y＝﹣3a，∵抛物线与线段BC恰有一个公共点，∴﹣3a＜4，a＞﹣，将x＝5代入抛物线得y＝12a，∴12a≥4，解得a≥；②a＜0时，如图2，将x＝0代入抛物线得y＝﹣3a，∵抛物线与线段BC恰有一个公共点，∴﹣3a＞4，解得a＜﹣；③当抛物线的顶点在线段BC上时，则顶点为（1，4），如图3，将点（1，4）代入抛物线得4＝a﹣2a﹣3a，解得a＝﹣1．综上所述，a≥或a＜﹣或a＝﹣1．23．（10分）解：（1）∵点C与C1重合，△ABC和△C1DE，∴△ABC和△CDE都是等边三角形，∴AC＝BC，CE＝CD，由旋转知，∠BCE＝∠ACD＝30°，在△BCE和△ACD中，，∴△BCE≌△ACD（SAS），∴BE＝AD，故答案案为：BE＝AD；（2）BE＝AD，证明：∵△ABC和△CDE都是等边三角形，∴AC＝BC，CE＝CD，由旋转知，∠BCE＝∠ACD，在△BCE和△ACD中，，∴△BCE≌△ACD（SAS），∴BE＝AD；（3）当点D在AC的延长线上时，AD最大，最大值为AC+CD＝a+b，即当α为180度时，线段AD的长度最大，最大值为a+b，当点D在线段AC上时，AD最小，最小值为AC﹣CD＝a﹣b，即当α为0度或360度时，线段AD的长度最小，最小值为a﹣b．