

福建省厦门市逸夫中学2021-2022学年八年级上学期期末数学试卷(含答案)
展开
厦门市逸夫中学2021-2022学年第一学期期末质量检测
八 年 级 数 学
(试卷满分:150分;考试时间:120分钟)
注意事项:
请把所有答案填涂或书写到答题卡上!请不要错位、越界答题!作图请用2B铅笔画出,并保留作图痕迹!在本试题上答题无效.
一、选择题(本大题共有10小题,每小题4分,共40分,在每小题所给出的四个选项恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
2.“”表示此类型的口罩能过滤空气中的粒径约为的非油性颗粒,其中用科学记数法表示为().
A. B. C. D.
3.2x3可以表示为( )
A.2x4﹣x B.x3+x3 C.x3•x3 D.2x6÷x2
4.袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
5.一个多边形的内角和为360°,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
6.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,可得△ABC≌△EDC,这时测得DE的长就是AB的长.判定△ABC≌△EDC最直接的依据是( )
A.HL B.SAS C.ASA D.SSS
7.一艘轮船顺水航行100km后返回,返回时用同样的时间只航行了80km,若列方程表示题中的等量关系,则关于方程中x和25这两个量的描述正确的是( )
A.x表示轮船在静水中的速度为x km/h
B.x表示水流速度为x km/h
C.25 表示轮船在静水中的速度为25 km/h
D.25 表示轮船顺水航行速度为25km/h
8.如图,将边长为的大正方形剪去一个边长为的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图所示长方形.这两个图能解释下列哪个等式( )
A. B. C. D.
9.把分式方程,的两边同时乘以x-2,约去分母,得( )
A.1-(1-x)=1 B.1+(1-x)=1 C.1-(1-x)=x-2 D.1+(1-x)=x-2
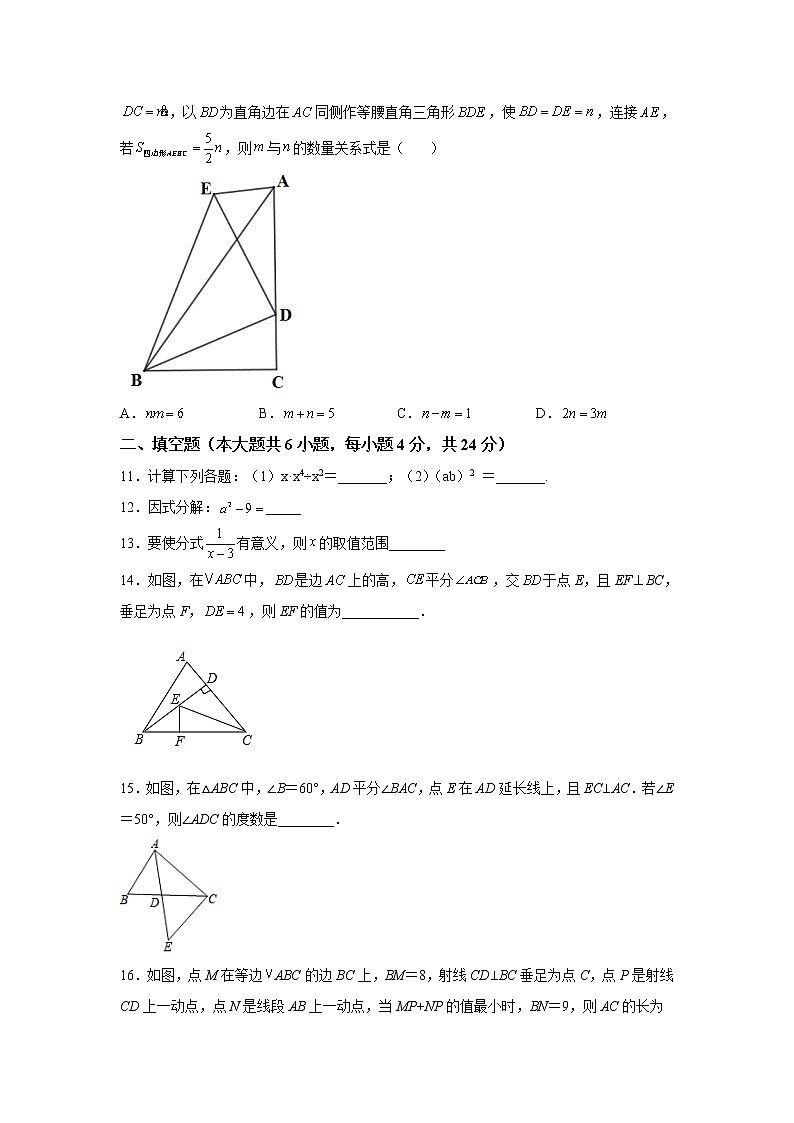
10.如图,中,,点在的边上,,以为直角边在同侧作等腰直角三角形,使,连接,若,则与的数量关系式是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题4分,共24分)
11.计算下列各题:(1)x·x4÷x2=_______;(2)(ab)2 =_______.
12.因式分解:_____
13.要使分式有意义,则的取值范围________
14.如图,在中,是边上的高,平分,交于点E,且EFBC,垂足为点F,,则EF的值为___________.
15.如图,在△ABC中,∠B=60°,AD平分∠BAC,点E在AD延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是________.
16.如图,点M在等边ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为_____.
三、解答题(本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤)
17.计算:
(1);
(2).
18.如图,已知点B,F,C,E在同一直线上,∥,,AB=ED,求证:.
19.先化简,再求值:,其中.
20.△ABC在平面直角坐标系中的位置如图所示(每个小正方形的边长为1).
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出点C1的坐标;
(3)若P(a,a-1)是△ABC内部一点,点P关于y轴对称点为P',且PP’=6,求点P'的坐标.
21.如图,已知△ABC,AC>AB,∠C=45°.
(1)尺规作图:在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹,不写作法)
(2)在(1)中延长BP到Q,使PQ=BP,连接QC,求证:QCBC.
22.京东快递仓库使用机器人分拣货物,已知一台机器人的工作效率相当于一名分拣工人工作效率的20倍,若用一台机器人分拣8000件货物,比原先16名工人分拣这些货物要少用小时.
(1)求一台机器人一小时可分拣多少件货物?
(2)受“双十一”影响,石家庄某京东仓库11月11日当天收到快递72万件,为了在8小时之内分拣完所有快递货物,公司调配了20台机器人和20名分拣工人,工作3小时之后,又调配了15台机器人进行增援,该公司能否在规定的时间内完成任务?请说明理由.
23.如图,在△ABC中,已知AB=BC,∠ABC=90°,点P是斜边AC上一点,作射线BP,过点A作ADBP于点D,过点C作CEBP于点E.
(1)依题意补全图形(不用尺规作图),并求证AD=BE;
(2)若AP=BC,△BPC的面积为9,求CE的长.
24.阅读材料一:可以展开成一个有规律的多项式:
;
;
;
;
……
阅读材料二:我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.下面我们依次对展开式的各项系数进一步研究发现,当取正整数时可以单独列成表中的形式:例如,在三角形中第二行的三个数1,2,1,恰好对应展开式中的系数,
(1)结合两个材料,写出的展开式:
(2)多项式的展开式是一个_____次_____项式?并预测第三项的系数是_____;
(3)请你猜想多项式取正整数)的展开式的各项系数之和,并进行合理说明(结果用含字母的代数式表示);
(4)利用材料中的规律计算:(不用材料中的规律计算不给分).
25.如图,等边△ABC中,点D为AB边上的一动点(D不与A、B重合).过点D作DE∥BC交AC于点E.把△ADE沿直线DE折叠,点A的对应点为P.
(1)求证:△ADE为等边三角形;
(2)连接AP,点D在运动过程中线段AP与线段DE是否存在一定的位置关系?证明你的结论;
(3)若等边△ABC的边长为3,当△BDP为直角三角形时,求的值.
参考答案
1.A
2.B
3.B
4.D
5.B
6.C
7.A
8.B
9.D
10.B
11. (1)x3; (2)a2b2.
【详解】
(1)x·x4÷x2=x5÷x2= x3;
(2)(ab)2 =a2b2
12.
【详解】
解:a2-9=(a+3)(a-3),
故答案为:(a+3)(a-3).
13.
【详解】
解:要使分式有意义,则,
解得,
故答案为:.
14.4
【详解】
解:是边上的高,
,
平分,且,
,
故答案为:4.
15.##100度
【详解】
解:,
,
平分,
,
,
,
故答案为:.
16.13
【详解】
解:∵△ABC是等边三角形,
∴AC=BC,∠B=60°,
作点M关于直线CD的对称点G,过G作GN⊥AB于N,交CD于P,
则此时,MP+PN的值最小,
∵∠B=60°,∠BNG=90°,
∴∠G=30°,
∵BN=9,
∴BG=2BN=18,
∴MG=BG-BM=18-8=10,
∴CM=CG=5,
∴AC=BC=13,
故答案为:13.
17.(1)3;(2).
【详解】
解:(1)原式
;
(2)原式
.
18.证明见解析.
【详解】
证明:,
,
在和中,,
,
.
19.,.
【详解】
解:原式
,
将代入得:原式.
20.(1)见解析;
(2)(-5,1);
(3)(-3,-4)
【分析】
(1)根据轴对称的性质得到点A1、B1、C1,顺次连线即可得到△A1B1C1;
(2)根据坐标系中位置直接得到;
(3)根据轴对称的性质得到P'(-a,a-1),由PP’=6,得到a-(-a)=6,求出a,即可得到点P'的坐标.
(1)
解:如图:
(2)
解:点C1的坐标为(-5,1);
(3)
解:∵P(a,a-1)是△ABC内部一点,点P关于y轴对称点为P',
∴P'(-a,a-1),
∵PP’=6,
∴a-(-a)=6,
解得a=3,
求点P'的坐标为(-3,-4).
21.(1)图见解析;(2)证明见解析.
【详解】
解:(1)如图,即为所作;
(2)如图,,
,
由(1)作图可知,,
又,
,
,
,
.
22.(1);(2)能在规定时间内完成任务,见解析
【详解】
(1)设一名工人每小时可分拣件货物,则一台机器人每小时可分拣件货物,
根据题意得:,
解得:,
经检验:是原方程的根,
∴,
答:一台机器人每小时可以分拣件货物;
(2)由(1)得台机器人和名分拣工小时的分拣量为:件
收到快递总件数为万件
未分拣的快递件数为:件
调配了台机器人进行增援
未分拣的件数由台机器人和名分拣工人分拣完所需的时间
解得:小时
分拣完万件快递需要的时间约为小时
该公司能在规定的时间内完成任务
23.(1)图见解析,证明见解析
(2)
【分析】
(1)先根据射线和垂线的作法补全图形,再根据直角三角形的性质可得,然后根据三角形全等的判定定理证出,最后根据全等三角形的性质即可得证;
(2)先根据等腰三角形的三线合一可得,再根据全等三角形的性质可得,设,从而可得,然后利用三角形的面积公式可得的值,由此即可得.
(1)
证明:补全图形如下:
,
,
,
在和中,,
,
;
(2)
解:,
(等腰三角形的三线合一),
由(1)已证:,
,
设,则,
的面积为9,
,即,
解得或(不符题意,舍去),
则.
24.(1)5,10,10,5
(2),,
(3),理由见解析
(4)1
(1)
解:由材料二得:,
故答案为:5,10,10,5;
(2)
解:是一次二项式,的展开式是二次三项式,的展开式是三次四项式,
则多项式的展开式是次项式,
由材料二的图可知,的第三项的系数是,
的第三项的系数是,
的第三项的系数是,
的第三项的系数是,
归纳类推得:的第三项的系数是,
故答案为:,,;
(3)
解:多项式取正整数)的展开式的各项系数之和为,理由如下:
的展开式的各项系数之和是,
的展开式的各项系数之和是,
的展开式的各项系数之和是,
的展开式的各项系数之和是,
归纳类推得:多项式的展开式的各项系数之和为;
(4)
解:
.
25.(1)见解析;(2)点D在运动过程中线段AP与线段DE互相垂直平分,见解析;(3)或
【详解】
解:(1)证明:∵△ABC为等边三角形,∴∠BAC=∠C=∠ABC=60°
又∵DE∥BC,∴∠ADE=∠ABC=60°,∠AED=∠C=60°,
∴∠ADE=∠AED=∠BAC=60° ,
∴△ADE为等边三角形.
(2)点D在运动过程中线段AP与线段DE互相垂直平分
证明:∵△ADE与△PDE关于直线DE成轴对称,
∴DE垂直平分AP,
∵△ADE为等边三角形,AP⊥DE,
∴AP平分DE,
∴ AP、DE互相垂直平分
(3)由于∠BDP=60°,所以,分∠BPD=90°或∠DBP=90°两种情况
① 当∠BPD=90°时,∵∠BDP=60°,∴∠PBD=30°,∴.
∵AD=PD, ∴ 即
②当∠DBP=90°时, 同理可得
即,
综上所述,当△BDP是直角三角形时,当或.
厦门市逸夫中学2021-2022学年七年级上学期期末质量检测数学试卷: 这是一份厦门市逸夫中学2021-2022学年七年级上学期期末质量检测数学试卷,共13页。
福建省厦门市逸夫中学2022-2023学年九年级上学期期中质量检测数学试卷: 这是一份福建省厦门市逸夫中学2022-2023学年九年级上学期期中质量检测数学试卷,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
福建省厦门市逸夫中学2022-2023学年九年级上学期期中质量检测数学试卷(含答案): 这是一份福建省厦门市逸夫中学2022-2023学年九年级上学期期中质量检测数学试卷(含答案),共28页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












