精品解析：黑龙江省哈尔滨方正县部分学校2021-2022学年七年级上学期期末联考数学试题-A4答案卷尾

这是一份精品解析：黑龙江省哈尔滨方正县部分学校2021-2022学年七年级上学期期末联考数学试题-A4答案卷尾，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

七年级上学期期末试卷
一、选择题（每题3分，共计30分）
1．2018的相反数是（     ）
A．2018 B．－ C． D．－2018
2．下列计算正确的是(            )
A．2a+3b=5ab B．3ab-2ba=ab C．6a2b−6ab2=0 D．2a2+3a3=5a5
3．在有理数：，2，0，-2中，最小的数是(            )
A． B．2 C．0 D．-2
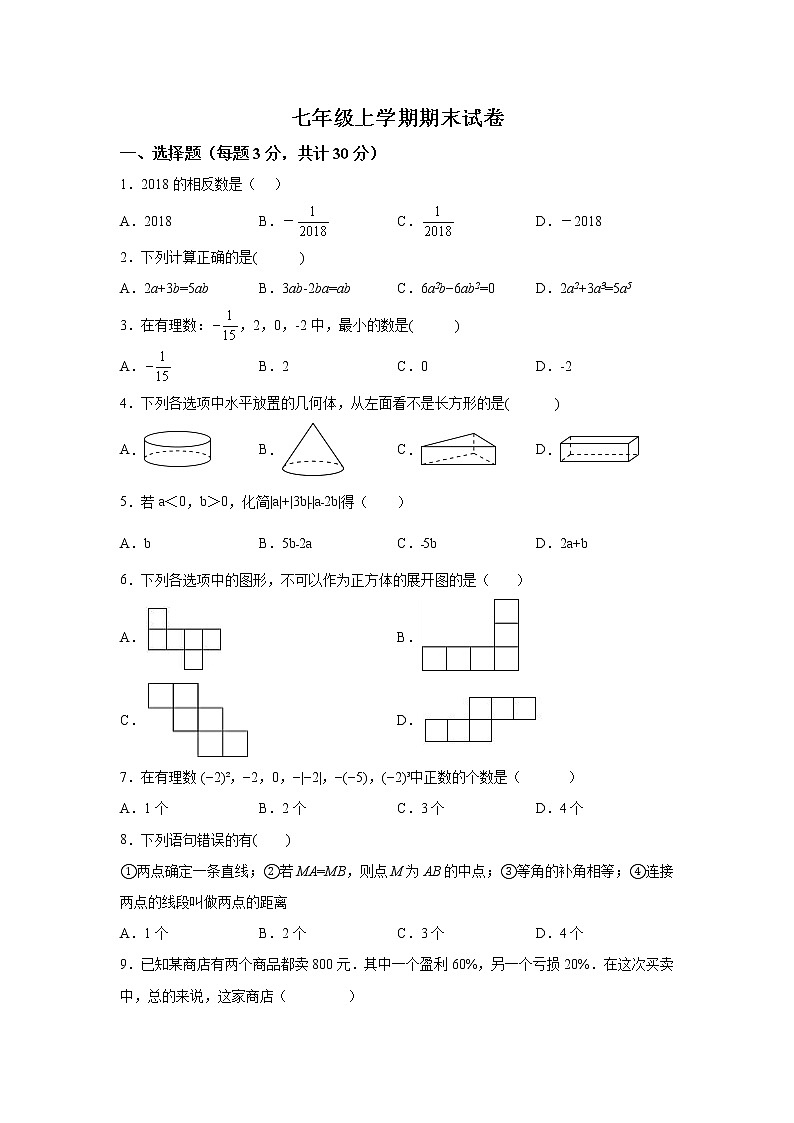
4．下列各选项中水平放置的几何体，从左面看不是长方形的是(             )
A． B． C． D．
5．若a＜0，b＞0，化简|a|+|3b|﹣|a﹣2b|得（　　）
A．b B．5b﹣2a C．﹣5b D．2a+b
6．下列各选项中的图形，不可以作为正方体的展开图的是（       ）
A． B．
C． D．
7．在有理数 (−2)²，−2，0，−|−2|，−(−5)，(−2)³中正数的个数是（             ）
A．1个 B．2个 C．3个 D．4个
8．下列语句错误的有(        )
①两点确定一条直线；②若MA=MB，则点M为AB的中点；③等角的补角相等；④连接两点的线段叫做两点的距离
A．1个 B．2个 C．3个 D．4个
9．已知某商店有两个商品都卖800元．其中一个盈利60%，另一个亏损20%．在这次买卖中，总的来说，这家商店（                 ）
A．盈利100元 B．亏损100元 C．不盈不亏 D．盈利200元
10．下列说法：①-a是负数；②两点确定一条直线；③的系数是2，次数是3；④38°15'大于38.15°；⑤射线AB和射线BA是同一条射线；⑥连接两点间的线段，叫做这两点间的距离，正确的个数是（       ）
A．1个 B．2个 C．3个 D．4个
二、填空题(每小题3分，共计30分)
11．的倒数是_____.
12．单项式的次数是____．
13．要在墙壁上固定一根小木条，至少需要两枚钉子，其数学原理是_____．
14．已知代数式的值是3，则代数式的值是______________
15．如果一个角的余角是50°，那么这个角的补角是________________．
16．一张试卷上有25道选择题：对一道题得4分，错一道得-1分，不做得-1分，某同学做完全部25题得70分，那么它做对题数为___________________
17．已知在数轴上A点表示数﹣2，B点表示数6，则AB的中点M在数轴上所对应的数_______
18．已知∠AOC=2∠BOC,若∠BOC=30°，则∠AOB=  _________
19．观察下列图形：它们是按一定规律排列的，依照此规律，第9个图形中共有___个★

20．如图，已知线段，点、分别是线段上的两点，且满足，点是线段的中点，求线段的长．

三、解答题(共计60分)
21．计算：
(1)(−2)²×2+(−2)³÷4
(2)×()×6÷2
解方程：
(1)7x-7=4x-5   
(2)−2=
22．先化简，再求值其中
23．若方程+=1−与关于x的方程2x−=m−6x解相同，求m的值．
24．如图，已知，∠AOB=120°，在∠AOB内画射线OC，∠AOC=40°．

（1）如图1，求∠BOC的度数；
（2）如图2，OD平分∠AOC，OE平分∠BOC，求∠DOE的度数．
25．某中学开学初到商场购买A、B两种品牌的足球，购买A种品牌的足球50个，B种品牌的足球25个，共花费4500元，已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元．
(1)求购买一个A种品牌、一个B种品牌的足球各需多少元?
(2)学校为了响应习总书记“足球进校园”的号召，决定第二次购买A、B两种品牌足球共50个，正好赶上商场对商品价格进行调整，A种品牌足球售价比第一次购买提高了4元，B种品牌足球按第一次购买时售价的九折出售，如果学校第二次购买A、B两种品牌足球的总费用是第一次购买足球总费用的70%，求学校第二次购买A种品牌的足球多少个?
26．如图，已知O为直线AB上一点，过点O向直线AB上方引三条射线OC、OD、OE，且OC平分∠AOD，∠2=3∠1．

(1)若∠AOD=140°，求∠1的度数．
(2)若∠1=15°，求∠COE的度数
(3)在(2)的条件下，若OF为一条过点O的射线，∠COF=2∠1，求∠BOF的度数．
27．如图，已知数轴上的点A对应的数为6，B是数轴上的一点，且AB=10，动点P从点A出发，以每秒6个单位长度的速度沿着数轴向左匀速运动，设运动时间为t秒(t>0)，

(1)数轴上点B对应的数是 ，点P对应的数是 (用t的式子表示)；
(2)动点Q从点B与点P同时出发，以每秒4个单位长度的速度沿着数轴向左匀速运动，试问：运动多少时间点P可以追上点Q？
(3)M是AP的中点，N是PB的中点，当点P在线段AB上运动时，线段MN的长度是否发生变化？若有变化，说明理由；若没有变化，请你画出图形，并求出MN的长．


1．D
【详解】
只有符号不同的的两个数互为相反数，由此可得2018的相反数是－2018，故选D.
2．B
【分析】
根据合并同类项法则，逐项判断即可求解．
【详解】
A、2a和3b不是同类项，无法合并，故本选项错误，不符合题意；
B、3ab-2ba=ab，故本选项正确，符合题意；
C、6a2b和6ab2不是同类项，无法合并，故本选项错误，不符合题意；
D、2a2和3a3不是同类项，无法合并，故本选项错误，不符合题意；
故选：B
【点睛】
本题主要考查了合并同类项，熟练掌握合并同类项法则是解题的关键．
3．D
【分析】
根据有理数的大小比较法则比较即可．
【详解】
根据有理数比较大小的方法，可得：，
故最小的有理数是−2．
故选：D．
【点睛】
本题考查了有理数大小比较的方法，解题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．
4．B
【分析】
根据左视图是从左面看到的视图，从而结合选项逐项判定左视图即可得到结论．
【详解】
解：A、圆柱的左视图是长方形，故本选项不符合题意
B、圆锥的左视图是等腰三角形，故本选项符合题意；
C、三棱柱的左视图是长方形，故本选项不符合题意；
D、长方体的左视图是长方形，故本选项不符合题意；
故选：B．
【点睛】
本题考查了简单几何体的三视图-左视图，熟练掌握常见几何体的三视图是解题的关键．
5．A
【分析】
直接利用绝对值的性质结合a，b的符号化简得出答案．
【详解】
解：∵a＜0，b＞0，
∴a﹣2b＜0，
∴|a|+|3b|﹣|a﹣2b|
＝﹣a+3b+a﹣2b
＝b．
故选A．
【点睛】
本题考查绝对值，正确掌握绝对值的性质是解题的关键．
6．B
【分析】
根据正方体展开图的特征进行判断即可．
【详解】
解：根据正方体展开图的“田凹应弃之”可得选项B中的图形不能折叠出正方体，
故选：B．
【点睛】
本题考查正方体的展开与折叠，掌握正方体展开图的特征是正确判断的前提．
7．B
【分析】
根据有理数的乘方化简，即可解答．
【详解】
解：（−2）2＝4，−|−2|＝−2，−（−5）＝5，（−2）3＝−8，
正数的个数有2个，
故选：B．
【点睛】
本题考查了有理数的乘方和绝对值的化简，解决本题的关键是有理数的乘方化简．
8．B
【分析】
根据直线的定义、线段中点的性质、补角的意义可进行排除选项．
【详解】
解：①两点确定一条直线，说法正确，故不符合题意；②若MA=MB，则点M为AB的中点，说法错误，有可能三点不在同一直线上，故符合题意；③等角的补角相等，说法正确，故不符合题意；④连接两点的线段长叫做两点的距离，原说法错误，故符合题意；
故选B．
【点睛】
本题主要考查直线的定义、线段中点的性质、补角的意义，熟练掌握直线的定义、线段中点的性质、补角的意义是解题的关键．
9．A
【分析】
设盈利60%的进价为x元，亏损20%的进价为y元，根据销售问题的数量关系建立方程求出其解即可．
【详解】
解：设盈利60%的进价为x元，亏损20%的进价为y元，由题意得：
x（1+60%）=800，y（1-20%）=800，
解得：x=500，y=1000，
∴成本为：500+1000=1500元．
∵售价为：800×2=1600元，
∴利润为：1600-1500=100元，
故选：A．
【点睛】
本题考查了列一元一次方程解实际问题的运用，根据题意得到等量关系是解题的关键．
10．B
【分析】
根据度分秒的进制，正数和负数，单项式，两点间的距离，直线、射线、线段，直线的性质，逐一判断即可．
【详解】
解：①-a可能是负数，正数或0，故①错误；
②两点确定一条直线，故②正确；
③的系数是，次数是3，故③错误；
④因为38.15°=38°9′，所以38°15'大于38.15°，故④正确；
⑤射线AB和射线BA不是同一条射线，故⑤错误；
⑥连接两点间的线段的长度，叫做这两点间的距离，故⑥错误；
上列说法中，正确的有2个，
故选：B．
【点睛】
本题考查了度分秒的换算，正数和负数，单项式，两点间的距离，直线、射线、线段，直线的性质，熟练掌握这些数学概念是解题的关键．
11．-5
【分析】
如果两个数互为倒数，则它们的乘积等于1.
【详解】
的倒数是，
故答案为-5.
【点睛】
本题考查倒数的概念.掌握倒数的概念是解决本题的关键.
12．4
【分析】
根据单项式中所有字母的指数的和是单项式的次数解答即可．
【详解】
解：单项式的次数是1+3=4，
故答案为：4．
【点睛】
本题考查单项式的次数，解答的关键是熟知单项式的次数是所有字母的指数的和．
13．两点确定一条直线
【分析】
根据两点确定一条直线解答．
【详解】
解：要在墙壁上固定一根小木条，至少需要两枚钉子，其数学原理是：两点确定一条直线，
故答案为:两点确定一条直线．
【点睛】
本题考查了直线的性质，熟记两点确定一条直线是解题的关键．
14．2
【分析】
前两项提取2变形后，把的值代入计算即可求出值．
【详解】
解：∵，
∴


．
故答案为：2
【点睛】
本题考查了代数式求值，熟练掌握运算法则是解本题的关键．
15．140°##140度

【分析】
先根据题意求出这个角的度数，再根据补角的定义求解即可．
【详解】
解：∵一个角的余角是50°，则这个角为90°-50°=40°，
∴这个角的补角的度数是180°-40°=140°．
故答案为：140°．
【点睛】
本题考查了余角和补角的定义，属于基础题，解题时牢记定义是关键，难度一般．
16．19
【分析】
设某同学做对题数为x道，那么他做错和不做的题数为（25-x）道题，他的得分应该是4x-（25-x）×1，据此可列出方程．
【详解】
解：某同学做对题数为x道，那么他做错和不做的题数为（25-x）道题，依题意有
4x-（25-x）×1=70，
解得x=19．
答：他做对题数为19．
故答案为：19．
【点睛】
本题考查了一元一次方程的应用，难度不大，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
17．2
【分析】
根据线段AB的中点M所表示的数为，即可解答.
【详解】
解：∵A点表示数-2，B点表示数6，
∴AB的中点M在数轴上所对应的数为：=2，
故答案为2.
【点睛】
本题考查了数轴，解决本题的关键是明确线段AB的中点M所表示的数为.
18．30 º或90 º
【分析】
分两种情况讨论：①当OC在∠AOB内部；②当OC在∠AOB外部，分别求得∠AOB的度数．
【详解】
①当OC在∠AOB内部时；
∵∠AOC=2∠BOC，∠BOC=30°，
∴∠AOC=60°，
∴∠AOB=30°+60°=90°；
②当OC在∠AOB外部时，
∵∠AOC=2∠BOC，∠BOC=30°，
∴∠AOC=60°，
∴∠AOB=60°-30°=30°；
故答案为30°或90°．
【点睛】
本题考查了角的计算，掌握分类讨论思想是解题的关键．
19．20
【分析】
观察图形可知后面一个图形比前面一个图形多2枚五角星，所以可得规律为：第n个图形中共有[4+2（n－1）]枚五角星．
【详解】
由图片可知：规律为五角星的总枚数=4+2（n－1）=2n+2．
n=9时，五角星的总枚数=2×9+2=20．
故答案为：20．
【点睛】
此题考查了规律型问题：图形的变化，是找规律题，目的是培养同学们观察、分析问题的能力．注意由特殊到一般的分析方法，此题的规律为：第n个图形中共有（2n+2）枚五角星．
20．25
【分析】
根据线段的比例，可用x表示AC，CD，DB，根据线段的和差，可得关于x的方程，根据解方程，可得x，再根据线段中点的性质，可得KC的长，根据线段的和差，可得答案．
【详解】
设AC＝3x，则CD＝4x，DB＝5x，
∵AB＝AC＋CD＋DB＝60
∴AB＝3x＋4x＋5x＝60．
∴x＝5．
∴AC＝15，CD＝20，
∵点K是线段CD的中点．
∴KC＝CD＝10．
∴AK＝KC＋AC＝25．
【点睛】
本题考查了两点间的距离，利用线段的和差得出关于x的方程是解题关键．
21．计算：（1）6；（2）；解方程：（1）；（2）x=2
【分析】
计算：（1）先计算乘方运算及乘除运算，然后计算加减运算即可；
（2）先计算乘方及小括号内的运算，然后计算乘除运算即可；
解方程：（1）直接进行移项合并同类项，系数化为1求解即可；
（2）先去分母，然后去括号，移项合并同类项，系数化为1求解即可．
【详解】
解：（1）原式=4×2+()÷
=8+（-2）
=6
（2）原式


解方程：
（1）7x-7=4x-5，
移项合并同类项得：3x=2
系数化为1得：x=；
（2），
去分母得：5（2x+1）-20=3x-1，
去括号得：10x+5-20=3x-1，
移项合并同类项得：7x=14
系数化为1得：x=2．
【点睛】
题目主要考查含乘方的有理数的混合运算及解一元一次方程，熟练掌握运算法则及求解方法是解题关键．
22．，-9
【分析】
先去括号，再合并同类项，然后再将x的值代入计算.
【详解】




当时，原式
【点睛】
此题考查整式的化简求值，依据整式的加减法法则正确化简整式是解题的关键.
23．m=13.2
【分析】
先求出第一个方程的解，把求出的x的值代入第二个方程，求出所得方程的解即可．
【详解】
解得：x=0.6，
将x=0.6代入，
得：，
解得：m=13.2．
即m的值为13.2．
【点睛】
本题考查了解一元一次方程和同解方程，解题关键是得出关于m的方程．
24．（1）80°；（2）60°
【分析】
（1）利用两个角的和进行计算即可；
（2）根据角平分线的意义和等式的性质，得出∠DOE═∠AOB即可．
【详解】
解：（1）如图1，

∵∠AOB =120°，∠AOC =40°；                            
∴∠BOC=∠AOB－∠AOC
=120°－40°=80°；
（2）如图2，

∵OD平分∠AOC，
∴∠AOD=∠COD=∠AOC
∵OE平分∠BOC，
∴∠BOE=∠COE=∠BOC      
∴∠DOE=∠COD+∠COE
=（∠AOC+∠BOC）
=∠AOB
=×120°
＝60°．
【点睛】
本题考查角平分线的意义，根据图形直观，得出角的和或差，是解决问题的关键．
25．(1)购买一个A种品牌的足球需要50元，购买一个B种品牌的足球需80元
(2)学校第二次购买A种品牌的足球25个

【分析】
（1）设A种品牌足球的单价为x元，B种品牌足球的单价为y元，根据“总费用=买A种足球费用+买B种足球费用，以及B种足球单价比A种足球贵30元”可得出关于x、y的二元一次方程组，解方程组即可得出结论；
（2）设购买B品牌足球m个，则购买A品牌足球（50-m）个，根据“A种品牌足球售价比第一次购买提高了4元，B种品牌足球按第一次购买时售价的九折出售，如果学校第二次购买A、B两种品牌足球的总费用是第一次购买足球总费用的70%”可得出关于m的一元一方程，解出m，由此即可得出结论．
（1）设A种品牌足球的单价为x元，B种品牌足球的单价为y元，依题意得，解得，答：A、B两品牌足球每个分别为50元、80元；
（2）设第二次购买A种品牌足球m个B种品牌足球(50-m)个，根据题意得(50+4)m+80×0.9×(50-m)=4500×70%m=25答：学校第二次购买A种品牌的足球25个．
【点睛】
本题考查了二元一次方程组的应用以及一元一次方程的应用，解题的关键是：（1）根据数量关系找出关于x、y的二元一次方程组；（2）根据数量关系找出关于m的一元一次议程．
26．(1)10°
(2)60°
(3)150°

【分析】
（1）先求出∠BOD的大小，再根据∠2＝3∠1求出∠1的大小；
（2）先求出∠BOD的大小，再求出∠AOD的大小，最后根据角平分线求出∠COE；
（3）先根据OF的位置，画出两种可能的图形，再分别计算．
（1）
解：∵∠AOD=140°，∠AOB=180°，
∴∠BOD=40°，
∵∠2=3∠1，∠2+∠1=∠BOD，
∴ ；
（2）
解：∵∠1=15°，∠2=3∠1，
∴∠BOD=∠1+∠2=4∠1=60°，
∴∠AOD=180°-∠BOD=120°，
∵OC平分∠AOD，
∴°，
∴∠COE=∠COD+∠1=75°；
（3）
解：∵∠COF=2∠1，
∴∠COF=30°，
当OF在OC右侧时，
∵∠DOF=∠COD-∠COF-30°，
∴∠BOF-∠DOF+∠BOD=90°，
当OF在OC左侧时，
∵∠DOF=∠COD+∠COF=90°，
∴∠BOF=∠DOF+∠BOD=150°．
【点睛】
本题考查角平分线中的角度计算．解题的关键是能够结合图形和角平分线的定义，表示各个角的数量关系．
27．(1)-4，6-6t
(2)t=5
(3)MN=5

【分析】
（1）根据点A对应的数为6，B是数轴上的一点，且AB=10，可得B点表示的数；点P表示的数为6-6t；
（2）根据题意可得：AP=6t，BQ=4t，根据点P追上点Q时，点P比点Q多运动10个单位，列出方程求解即可；
（3）利用中点的定义和线段的和差，求出MN，即可求解．
（1）解：点A对应的数为6，且AB=10，∴点B对应的数是6-10=-4；∵点P从点A出发，以每秒6个单位长度的速度沿着数轴向左匀速运动，∴AP=6t，∴点P对应的数是6-6t；故答案为：-4，6-6t；
（2）解：根据题意得：AP=6t，BQ=4t，∴6t-4t=10，解得：t=5；即运动5秒，点P可以追上点Q；
（3）解：线段MN的长度不发生变化．理由如下：∵M是AP的中点，N是PB的中点，∵，，∵AB=10，∴MN=5．
【点睛】
本题考查了数轴上的动点问题，一元一次方程的应用以及数轴上两点之间的距离，利用数形结合思想解答是解题的关键．