





八年级上册第十五章 分式15.3 分式方程多媒体教学课件ppt
展开【学习目标】1.学会用分式方程解决比较简单的实际问题并会验根.2.以工程问题为例,能将此类实际问题中的相等关系用分式方程表示,提高学生运用方程思想解决问题的能力.3.通过对实际问题的分析,进一步感受分式方程是刻画现实世界的有效模型.
【学习重点】1.实际生活中相关工程问题类的分式方程应用题的分析应用.2.建立数学模型,列分式方程解决行程问题和销售问题.
我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
(1)行程问题: 路程=速度×时间以及它的两个变式;
(2)数字问题: 在数字问题中要掌握十进制数的表示法;
(3)工程问题: 工作量=工时×工效以及它的两个变式;
(4)顺逆问题: 顺速=静速+水速;逆速=静速-水速;
(5)利润问题:批发成本=批发数量×批发价;批发数量=批发成本÷批发价;打折销售价=定价×折数;销售利润=销售收入一批发成本;每本销售利润=定价一批发价;每本打折销售利润=打折销售价一批发价,利润率=利润÷进价。
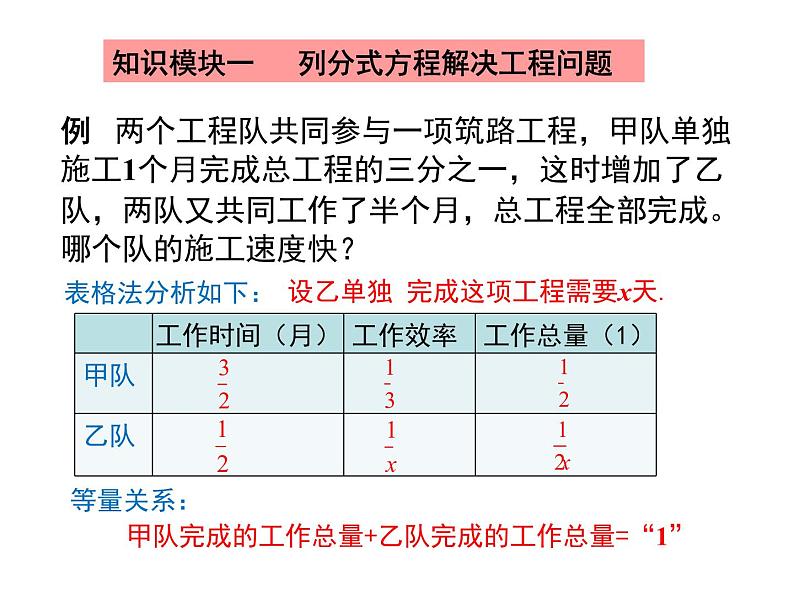
例 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独 完成这项工程需要x天.
知识模块一 列分式方程解决工程问题
方程两边都乘以6x,得
检验:当x=1时,6x≠0.所以,原分式方程的解为x=1.由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
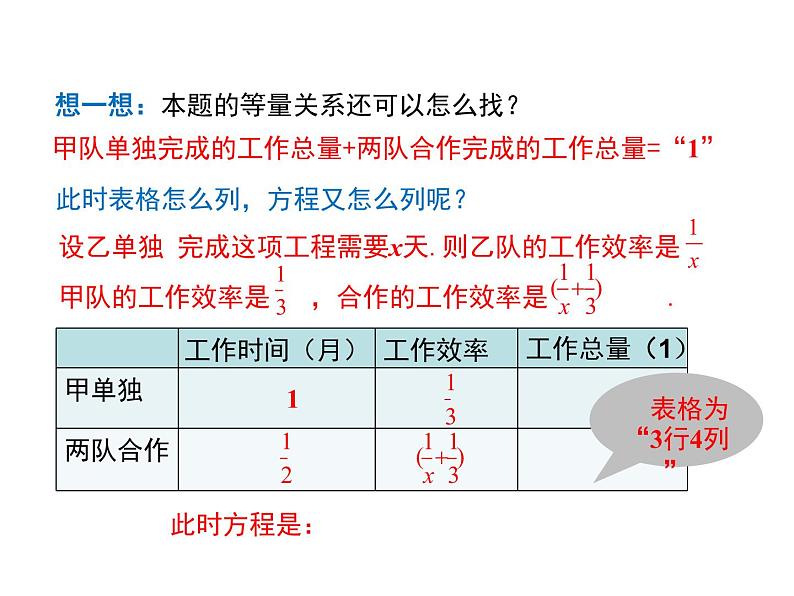
想一想:本题的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
此时表格怎么列,方程又怎么列呢?
设乙单独 完成这项工程需要x天.则乙队的工作效率是 甲队的工作效率是 ,合作的工作效率是 .
表格为“3行4列”
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如× ×单独完成需 x(单位时间),则可表示出其工作效率;
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如行程问题有工作效率,工作时间,工作量;2指该类问题中的“两个主人公”如甲队和乙队,或“甲单独和两队合作”;1指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
3.弄清基本的数量关系.如本题中的“合作的工效=甲乙两队工作效率的和”.
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.2.设:选择恰当的未知数,注意单位和语言完整.3.列:根据数量和相等关系,正确列出方程.4.解:认真仔细解这个分式方程.5.验:检验.(第一:是否是分式方程的解, 第二 :是否符合题意)6.答:注意单位和语言完整.
练习 某工程队需要在规定日期内完成任务。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
等量关系:甲工作量+乙工作量=1
解:设规定日期是x天,得
经检验,x=6是原分式方程的解
例 某次列车平均提速v千米/时,用相同的时间,列车提速前行使s千米,提速后比提速前多行使50千米,提速前列车的平均速度为多少?
设提速前列车的平均速度为x千米/时.
提速前行驶时间=提速后行驶时间
知识模块二 列分式方程解决行程问题
解:设提速前列车的平均速度为x千米/时,根据题意得
答:提速前列车的速度为 千米/时.
1.注意关键词“提速”与“提速到”的区别;
2.明确两个“主人公”的行程问题中三个量用代数式表示出来;
3.行程问题中的等量关系通常抓住“时间线”来建立方程。
列分式方程解应用题的一般步骤
1.审:清题意,并设未知数; 2.找:相等关系,3.列:出方程;4.解:这个分式方程;5.验:根(包括两方面 :(1)是否是分式方程的根;(2)是否符合题意);6.写:答案.
列分式方程解决实际问题有什么方法技巧?
列分式方程解应用题的基本思路和列整式方程解应用题的基本思路是相同的,关键步骤是根据题意寻找“等量关系”.
同时,解出分式方程后注意检验求出的值是不是方程的解,是否符合实际意义.
P154习题3 甲、乙两人分别从相距目的地6千米和10千米的两地同时出发,甲、乙的速度比是3:4,结果甲比乙提前20分到达目的地。求甲、乙的速度。
解:设甲速度为3x千米/时,乙速度为4x千米/时
解:设甲的速度3x千米/时,则乙的速度是4x千米/时,得
答:甲的速度4.5千米/时,乙的速度是6千米/时。
经检验,x=1.5是原分式方程的解
∴ 3x=4.5 ,4x=6
P155习题4 A、B两种机器人都被用来搬运化工原料,A型 机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
解:设机器人A每小时搬运xkg
等量关系:第二组用的时间-第一组用的时间=15分钟
练习 两个小组同时开始攀登一座450米高的山,第一组的速度是第二组的1.2倍,他们比第二组早15分到达顶峰,两个小组的速度各是多少? (若山高h米,第一组的速度是第二组的a倍,并比第二组早t分到达顶峰,则两组速度各是多少?)
解:设第二组的速度为x米/分
1. A,B两地相距135千米,有大,小两辆汽车从A地开往B地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟.已知大、小汽车速度的比为2:5,求两辆汽车的速度.
2. 某工人师傅先后两次加工零件各1500个,当第二次加工时,他革新了工具,改进了操作方法,结果比第一次少用了18个小时.已知他第二次加工效率是第一次的2.5倍,求他第二次加工时每小时加工多少零件?
初中数学人教版八年级上册15.3 分式方程优质课件ppt: 这是一份初中数学人教版八年级上册15.3 分式方程优质课件ppt,文件包含人教版初中数学八年级上册1532分式方程的应用课件pptx、人教版初中数学八年级上册1532分式方程的应用分层练习docx、人教版初中数学八年级上册1532分式方程的应用教案docx、人教版初中数学八年级上册1532分式方程的应用预习案docx等4份课件配套教学资源,其中PPT共36页, 欢迎下载使用。
初中数学人教版八年级上册15.3 分式方程课文ppt课件: 这是一份初中数学人教版八年级上册15.3 分式方程课文ppt课件,共19页。PPT课件主要包含了例题欣赏,15x等内容,欢迎下载使用。
初中数学人教版八年级上册15.3 分式方程图文ppt课件: 这是一份初中数学人教版八年级上册15.3 分式方程图文ppt课件,共19页。PPT课件主要包含了解得x=2000等内容,欢迎下载使用。













