






华师大版七年级下册第7章 一次方程组7.4 实践与探索教学演示ppt课件
展开2.进一步经历和体验列方程组解决实际问题的过程,体会方程组是刻画现实世界数量关系的有效数学模型,发展模型思想和应用意识.
1.能借助表格分析较为复杂问题中的数量关系,建立方程组解决问题.
1.列二元一次方程组解决实际问题的步骤是什么?2.列二元一次方程组解决实际问题的关键是什么?
(1)认真审清题意,分析等量关系;(2)设两个未知数;(3)根据等量关系列方程,联立成方程组;(4)解方程组;(5)检验所得的解是否为方程组的解,是否符合题意;(6)作答(注意写单位).
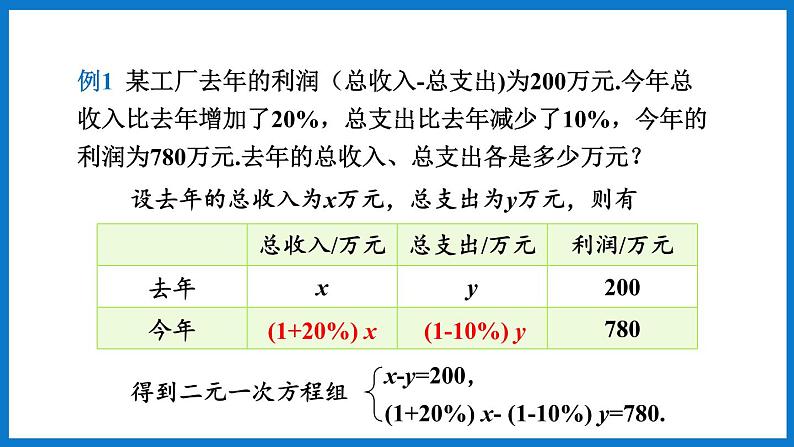
例1 某工厂去年的利润(总收入-总支出)为200万元.今年总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总收入、总支出各是多少万元?
去年的总收入-去年的总支出=200万元,今年的总收入-今年的总支出=780万元,
今年的总收入=去年的总收入×(1+20%),今年的总支出=去年的总支出×(1-10%).
设去年的总收入为x万元,总支出为y万元,则有
x-y=200,(1+20%) x- (1-10%) y=780.
解:设去年的总收入为x万元,总支出为y万元.
根据等量关系列方程组为
x-y=200 ,(1+20%) x- (1-10%) y=780 .
x-y=200,4x-3y=2 600.
x=2 000,y=1 800.
答:去年的总收入为2 000万元,总支出为1 800万元.
每餐甲原料中含蛋白质量+每餐乙原料中含蛋白质量=35单位,每餐甲原料中含铁质量+每餐乙原料中含铁质量=40单位.
例2 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质.若病人每餐需要35单位蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰好满足病人的需要?
设每餐需甲原料x g,乙原料y g,则有
解:设每餐需甲原料x g,乙原料y g.
0.5x+0.7y=35, x+0.4y=40.
5x+7y=350, 5x+2y=200.
答:每餐需甲原料28g,乙原料30g.
图表分析有利于理清题中的未知量,已知量以及等量关系,条理清楚.
1.根据题意绘制图表,理清题中的未知量.
2.根据绘制图表,整理出等量关系式.
3.列出方程组,解决实际问题.
1.对于较复杂的问题,可以通过列表格的方法理清题中的未知量,已知量以及等量关系,条理清楚.
2.要注意的是,处理实际问题的方法是多种多样的,图表分析是一种直观简洁的方法,应根据具体问题灵活选用.
1.某公司用30 000元购进甲、乙两种货物.货物卖出后,甲种货物获利10%,乙种货物获利11%,共得利润3 150元,问两种货物各进多少钱的货?设甲种货物进x元的货,乙种货物进 y元的货,填写下表并求出x,y的值.
答:甲种货物进15 000元的货,乙种货物进15 000元的货.
3 100 ×(1+4.4%)
2.学校去年有学生3 100名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名?设该校去年有寄宿学生x名,走读学生y名,填写下表并求出x,y的值.
初中数学华师大版七年级下册第7章 一次方程组7.4 实践与探索课文内容ppt课件: 这是一份初中数学华师大版七年级下册<a href="/sx/tb_c15959_t3/?tag_id=26" target="_blank">第7章 一次方程组7.4 实践与探索课文内容ppt课件</a>,共19页。PPT课件主要包含了解方程组得,x23y7,x30y10等内容,欢迎下载使用。
初中数学华师大版七年级下册7.4 实践与探索优秀ppt课件: 这是一份初中数学华师大版七年级下册<a href="/sx/tb_c15959_t3/?tag_id=26" target="_blank">7.4 实践与探索优秀ppt课件</a>,文件包含74实践与探索pptx、74实践与探索教学设计doc、74实践与探索学案doc等3份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
数学七年级下册第6章 一元一次方程6.3 实践与探索说课ppt课件: 这是一份数学七年级下册第6章 一元一次方程6.3 实践与探索说课ppt课件,文件包含第2课时一元一次方程的实际应用pptx、第3课时一元一次方程的实际应用pptx、第1课时一元一次方程的实际应用pptx等3份课件配套教学资源,其中PPT共70页, 欢迎下载使用。













