初中数学华师大版七年级下册9.2 多边形的内角和与外角和课堂教学ppt课件

这是一份初中数学华师大版七年级下册9.2 多边形的内角和与外角和课堂教学ppt课件，文件包含第1课时多边形及其内角和pptx、第2课时多边形的外角和pptx等2份课件配套教学资源，其中PPT共30页， 欢迎下载使用。

了解多边形的外角概念，知道与每个内角相邻的外角分别有两个；通过探索多边形的外角和，掌握多边形的外角和公式、内角和公式的应用.
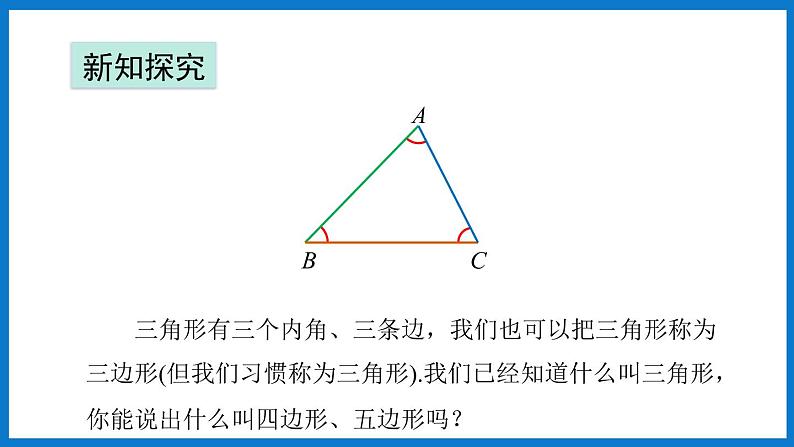
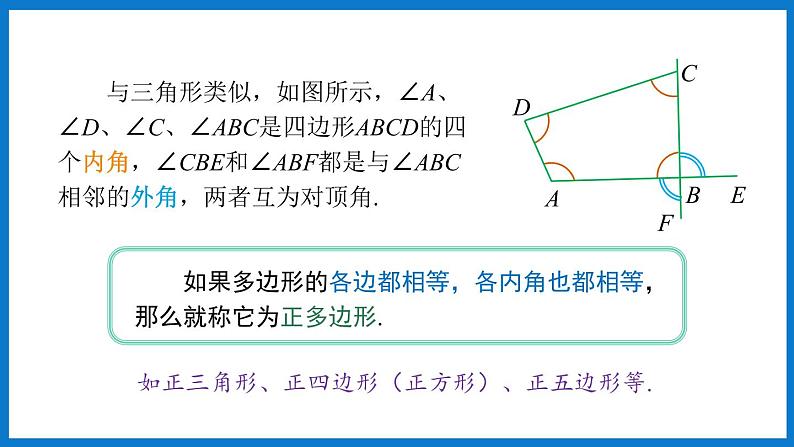
1.与三角形的每个内角相邻的外角有几个？它们是什么关系？三角形外角和的定义是什么？
2.n边形的内角和为___________.
与三角形的每个内角相邻的外角分别有两个，这两个外角是对顶角. 从与每个内角相邻的两个外角中分别取一个相加，得到的和称为三角形的外角和.
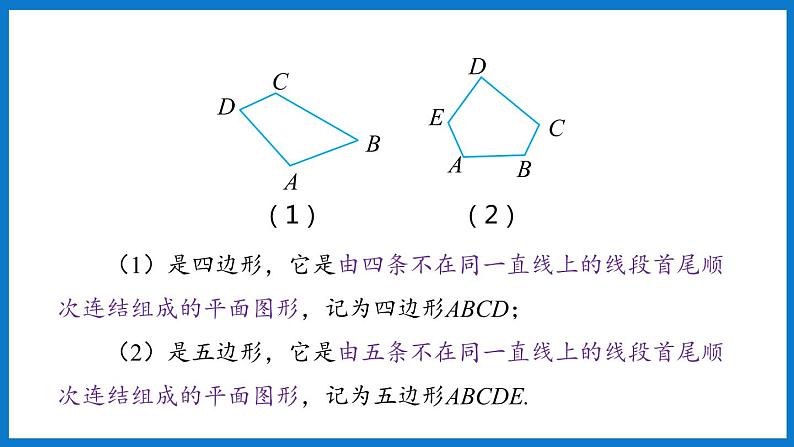
类比三角形的外角知识，你能得到关于多边形的外角知识吗？
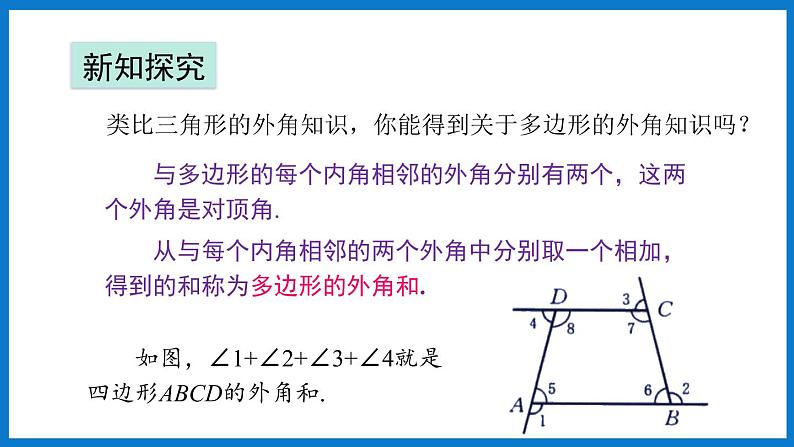
与多边形的每个内角相邻的外角分别有两个，这两个外角是对顶角. 从与每个内角相邻的两个外角中分别取一个相加，得到的和称为多边形的外角和.
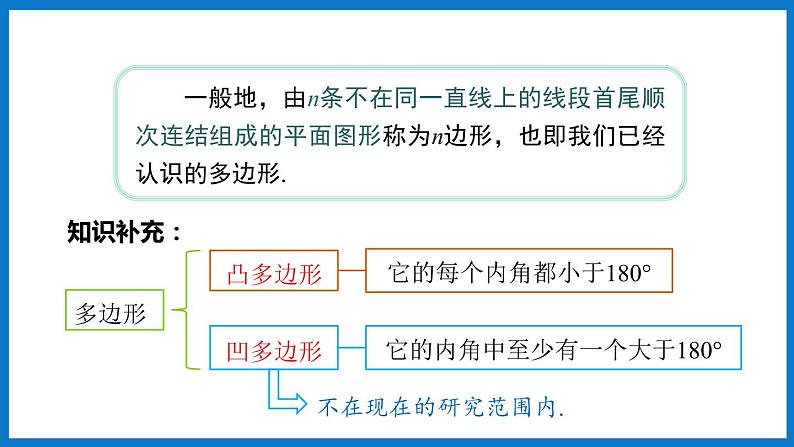
如图，∠1+∠2+∠3+∠4就是四边形ABCD的外角和.
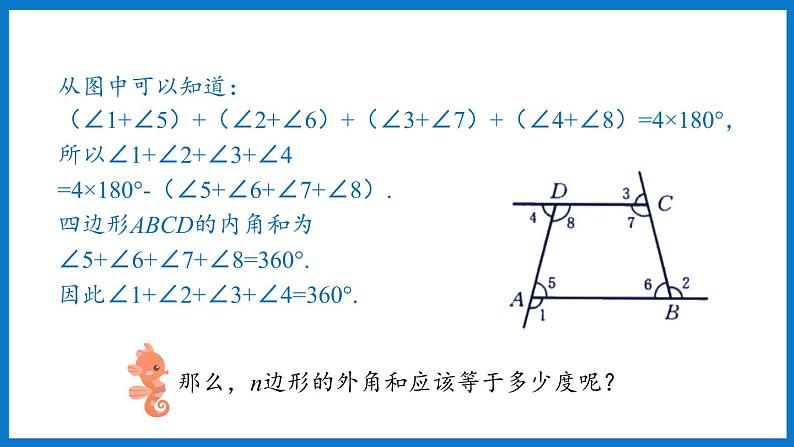
从图中可以知道：（∠1+∠5）+（∠2+∠6）+（∠3+∠7）+（∠4+∠8）=4×180°，所以∠1+∠2+∠3+∠4=4×180°-（∠5+∠6+∠7+∠8）.四边形ABCD的内角和为∠5+∠6+∠7+∠8=360°.因此∠1+∠2+∠3+∠4=360°.
那么，n边形的外角和应该等于多少度呢？
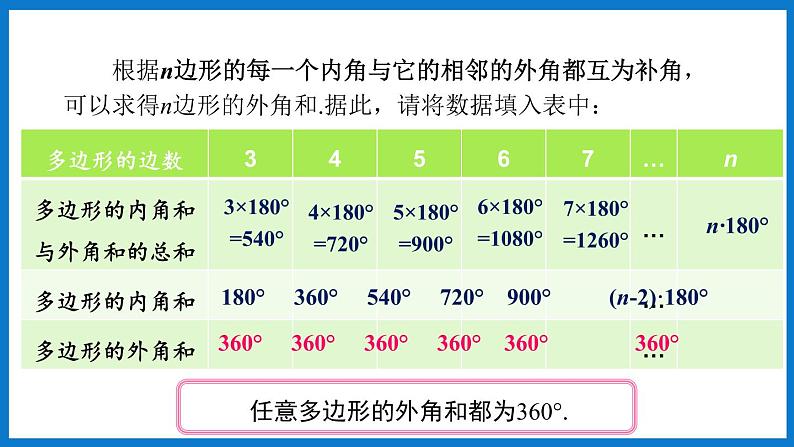
根据n边形的每一个内角与它的相邻的外角都互为补角，可以求得n边形的外角和.据此，请将数据填入表中：
3×180°=540°
4×180°=720°
5×180°=900°
6×180°=1080°
7×180°=1260°
180° 360° 540° 720° 900° (n-2)·180°
360° 360° 360° 360° 360° 360°
例1 一个多边形的每个外角都是72°，这个多边形是几边形？
解：设多边形的边数为n，根据题意，得 　 n·72°=360°.解得 n=5.因此，这个多边形是五边形.
例2 一个多边形的内角和等于它外角和的5倍，这个多边形是几边形？
解：设多边形的边数为n，根据题意，得 （n-2）·180°=5×360°.解得 n=12.因此，这个多边形是十二边形.
多边形的内角和与外角和的两点区别
（1）多边形的内角和是指所有内角的度数之和，而它的外角和是各个顶点处只取一个外角的和.（2）多边形的内角和与边数有关，而其外角和与边数无关.由多边形的边数可求得其内角和，反之亦可，而由外角和无法确定多边形的边数（已知外角度数，且外角均相等的多边形除外）.
____________________________________________，得到的和称为多边形的外角和.
与多边形的每个内角相邻的外角分别有_______，它们是_________.
任意多边形的外角和都为_______.
从与每个内角相邻的两个外角中分别取一个相加
1.如图，一个四边形的三个外角分别为110°，85°，30°，则∠α等于（ ） A.30° B.45°C.70° D.85°
解析：因为∠α的外角为180°-∠α，由“任意多边形的外角和都为360°”，知(180°-∠α)+110°+85°+30°=360°，解得∠α=45°.
2.一个多边形的内角和加上它的外角和等于900°，求此多边形的边数.
解：设这个多边形的边数是n，则(n-2)×180°+360°=900°，解得 n=5.所以此多边形的边数为5.
3.一个正多边形的每个内角比相邻外角大36°，求这个正多边形的边数.
解：设内角为x°，则外角为（x-36）°，根据题意得 x+x-36=180，解得 x=108，则外角为 108°-36°=72°，所以这个正多边形的边数为：360°÷72°=5.