华师大版七年级数学下册9.3 用正多边形铺设地面（课件）

这是一份华师大版七年级数学下册9.3 用正多边形铺设地面（课件），共27页。

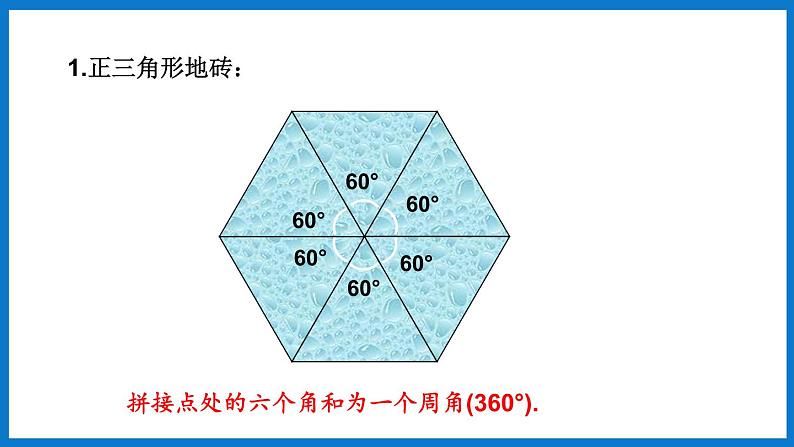
第9章 多边形9.3 用正多边形铺设地面1. 进一步巩固多边形内角和与外角和公式；2. 掌握用相同的正多边形铺满地面的条件；3. 掌握用多种正多边形铺满地面的条件.1.什么叫正多边形？① n 边形的内角和公式：(n – 2)×180°.② n 边形的外角和：360°.③正 n 边形每个内角度数：如果多边形的各边都相等，各内角也都相等，那么就称它为正多边形.2.完成下列问题：  小明家最近装修房子，客厅准备用同一种正多边形的地砖来铺设，卧室准备用多种正多边形的地砖来铺设.现有正三角形、正四边形、正五边形、正六边形和正八边形五种地砖可供选择，那么哪些正多边形地砖可分别用来铺设客厅和卧室呢？探究一：用相同的正多边形铺设地面请各小组拿出准备好的正三角形、正四边形、正五边形、正六边形和正八边形卡片，拼一拼，看看哪些能铺满地面，哪些不能.探究一：用相同的正多边形铺设地面经过动手验证，结果如下：正三角形正四边形正五边形正六边形正八边形√√√××思考：1.正三角形地砖：拼接点处的六个角和为一个周角(360°).2.正四边形地砖：拼接点处的四个角和为一个周角(360°).3.正五边形地砖：拼接点处的三个或四个角的和不是一个周角.4.正六边形地砖：拼接点处的三个角和为一个周角(360°).5.正八边形地砖：拼接点处的三个角的和不是周角.有重叠使用给定的某种正多边形，当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时，就可以铺满地面.探究二：用多种正多边形铺设地面两种正多边形铺设地面1.正三角形和正四边形(1)90°+60°+90°+60°+60°=360°.1.正三角形和正四边形(2)90°+90°+60°+60°+60°=360°.2.正三角形和正六边形(1)120°+120°+60°+60°=360°.2.正三角形和正六边形(2)120°+60°+60°+60°+60°=360°.3.正四边形和正八边形135°+135°+90°=360°.三种正多边形铺设地面探究二：用多种正多边形铺设地面正六边形、正四边形和正三角形.120°+90°+90°+60°=360°.正多边形的组合能否铺满地面，关键是看位于同一顶点处的几个内角之和是否为360°.若是，则说明能铺满，否则说明不能铺满.1. 用一种正多边形能进行平面铺设的条件是( )A. 内角都是整数度数B. 边数是 3 的整数倍C. 内角整除 180°D. 内角整除 360°D2. 下列不能铺满地面的正多边形组合是( )A. 正三角形和正方形B. 正三角形和正六边形C. 正方形和正八边形D. 正五边形和正八边形D3.用正十二边形能铺满地面吗？为什么？解：用正十二边形不能铺满地面.因为正十二边形的每一个内角的度数为150°，而360°不能被150°整除，即由150°的整数倍不能得到一个周角，故不能铺满地面.4.同时用正五边形和正六边形组合能否铺满地面？为什么？解：不能.因为正六边形的每个内角为120°，而正五边形的每个内角为108°，假设m个正五边形和n个正六边形能铺满地面，则m·108°+n·120°=360°，化简，得9m+10n=30，不存在m,n均为正整数，使等式成立.故不能铺满地面.使用给定的某种正多边形，当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时，就可以铺满地面.用相同的正多边形铺设地面用多种正多边形铺设地面对于情境引入中的问题，针对小明家客厅及卧室的地砖选择，你能给出什么建议呢？