中考总复习数学（安徽地区）-第7章尺规作图课件

这是一份中考总复习数学（安徽地区）-第7章尺规作图课件，共60页。PPT课件主要包含了目录安徽·中考，考点尺规作图，命题角度尺规作图，尺规作图，命题角度，考点1，三视图，考点2，长对正，高平齐等内容，欢迎下载使用。

1.尺规作图的工具 没有刻度的直尺和圆规.
2.五种基本的尺规作图 (1)作一条线段等于已知线段
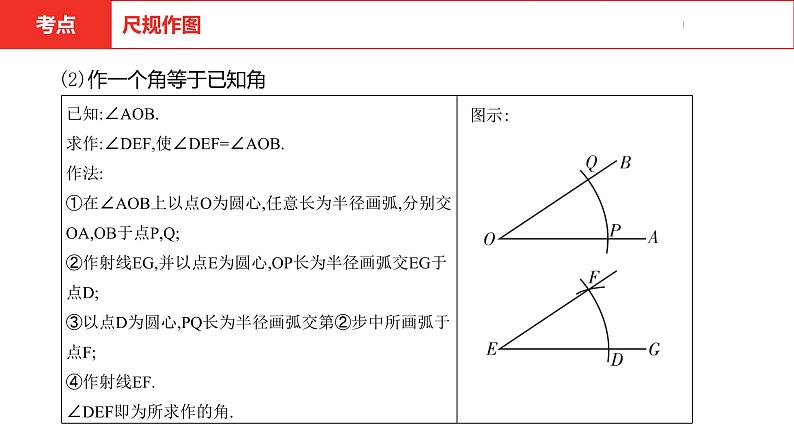
(2)作一个角等于已知角
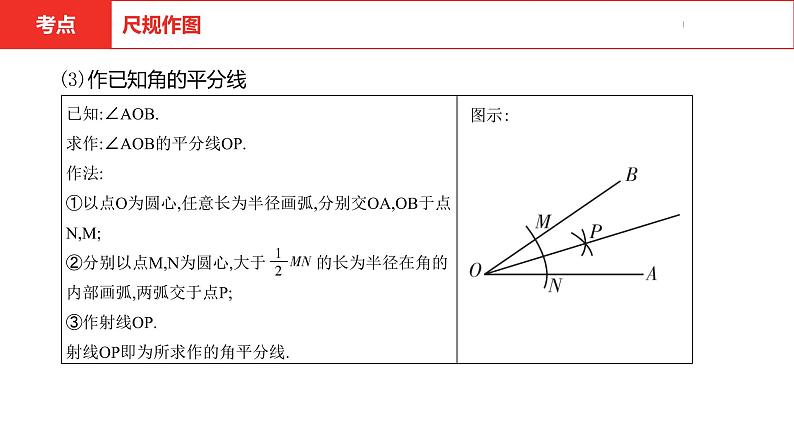
(3)作已知角的平分线
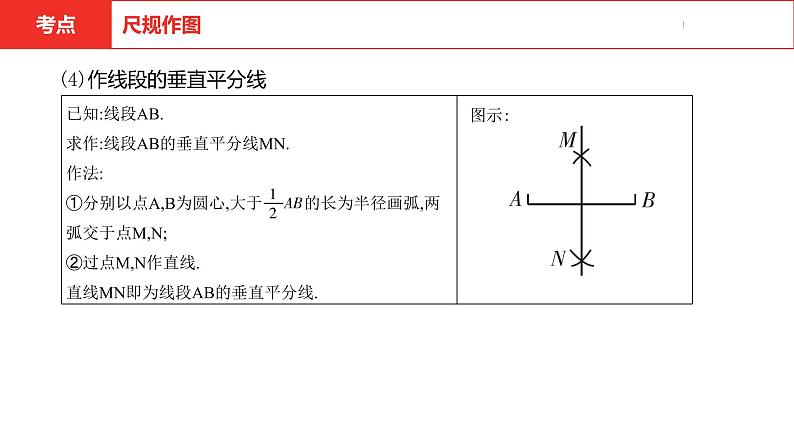
(4)作线段的垂直平分线
(5)经过一点作已知直线的垂线 ①经过已知直线上的一点作这条直线的垂线.
②经过已知直线外一点作这条直线的垂线
例[2020山东济宁]如图,在△ABC中,AB=AC,点P在BC上.(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若∠APC=2∠ABC,求证:PD∥AB.
【思路分析】　(1)根据三角形相似得到对应角相等,再根据利用尺规作一个角等于已知角的方法作图即可.(2)利用相似三角形的性质及平行线的判定定理求证即可.
(1)△PCD如图所示.(2)证明:∵∠APC=∠ABC+∠BAP=2∠ABC,∴∠BAP =∠ABC.又∠BAP=∠CPD,∴∠CPD=∠ABC,∴PD∥AB.
第二节 投影与视图
考点1 投影考点2 三视图考点3 几何体的展开与折叠
命题角度1 常见几何体的三视图命题角度2 由三视图还原几何体
一个物体放在阳光下或者灯光前,就会在地面上或者墙面上留下它的影子,这个影子称为物体的投影.
1.视图一个几何体在一个平面上的正投影叫做这个几何体的视图.
3.三视图画法的规律主视图与俯视图要①　　　　, 主视图与左视图要②　　　　, 俯视图与左视图要③　　　　. 注:看得见的部分的轮廓线要画成④　　　　,看不见的画成⑤　　　　.
4.常见几何体的三视图
5.由三视图确定几何体由三视图想象几何体时,首先分别根据主视图、左视图、俯视图想象几何体的正面、左侧和底面,然后综合起来考虑整体.
1.常见几何体的展开图
2.正方体展开图的常见类型
一个几何体能展开成一个平面图形,这个平面图形就可以折叠成相应的几何体,展开和折叠是一个互逆的过程.
1.[2020广西河池]下列立体图形中,主视图为矩形的是(　　)
2.[2020天津]如图是一个由5个相同的正方体组成的立体图形,它的主视图是(　　)
3.[2020辽宁抚顺]如图是由一个长方体和一个圆锥组成的几何体,它的主视图是(　　)
4.[2020山东青岛]如图所示的几何体,其俯视图是(　　)
5.[2020北京]如图是某几何体的三视图,该几何体是(　　)
6.[2020湖北宜昌]诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图是对某物体从不同角度观察的记录情况,对该物体的判断最接近本质的是(　　)
A.圆柱 B.圆锥 C.三棱柱D.长方体
A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管C.是圆柱形物体,里面有两个垂直的空心管D.是圆柱形物体,里面有两个平行的空心管
第三节 图形的对称、平移、旋转与位似
考点1 轴对称与轴对称图形考点2 图形的中心对称考点3 图形的平移与旋转变换考点4 位似图形
命题角度1 图形的对称命题角度2 图形的平移命题角度3 图形的旋转命题角度4 网格作图
1.轴对称与轴对称图形
2.折叠的性质(1)位于折痕两侧的图形关于折痕成轴对称;(2)折叠前后的两部分图形全等,对应边、对应角、对应线段均相等,周长、面积均相等;(3)折叠前后,非重合对应点的连线均被折痕所在直线垂直平分.
3.常见的轴对称图形及其对称轴
4.作轴对称图形的一般步骤(1)找:在原图形上找关键点(如线段的端点、线与线的交点等);(2)作:作各个关键点关于已知直线(对称轴)的对称点;(3)连:按原图形依次连接各关键点的对称点.
1.中心对称与中心对称图形
2.常见的中心对称图形及其对称中心
1.定义 如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,那么这两 个图形叫做位似图形,这个点叫做　 　　　,此时的相似比又称为　　　　 .如图,五边形ABCDE与五边形A'B'C'D'E'是位似图形.
2.性质(1)对应点的连线或其延长线都相交于同一点(位似中心);(2)位似图形对应边平行或共线,且成比例;(3)位似图形上任意一对对应点到位似中心的距离之比等于　　　 　,位似图形的面积比等于　 　　　; (4)位似图形是具有特殊位置关系的相似图形,具有相似图形的一切性质.
3.在网格中作位似图形的步骤(1)确定位似中心;(2)连接位似中心和原图形的关键点并延长或反向延长;(3)根据位似比,确定原图形关键点的对应点;(4)按原图形顺次连接所作各点,得到放大或缩小的图形.
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的同侧,位似中心只有一个.
例1 [2020广东]如图,在正方形ABCD中,AB=3,点E,F分 别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF 折叠,点B恰好落在AD边上的B'处,则BE的长度为 (　　) A.1 B. C.D.2
解决折叠问题的一般思路1.找出隐含的折叠前后的位置关系(平行或垂直)和数量关系(相等);2.一般运用全等三角形、勾股定理、相似三角形等知识及方程思想,设出恰当的未知数,解方程来求得答案.当折叠问题中涉及分类讨论时,应注意以下问题:(1)要先考虑分哪些情况,画出各种情况所对应的图形,再作出适当的辅助线,根据题中的等量关系,通过勾股定理、相似三角形等列出方程,求得答案;(2)在分类讨论时,可先画出折叠后对应点的轨迹,再确定满足题干条件的情况,这样不仅能避免遗漏答案,而且还能快速确定分类情况.
例2[2020浙江台州]如图,把△ABC先向右平移3个单位 长度,再向上平移2个单位长度,得到△DEF,则顶点 C(0,-1)对应点的坐标为 (　　) A.(0,0) B.(1,2) C.(1,3)D.(3,1)
【思路分析】　利用点的平移规律求解即可.
解决与平移相关的问题的方法平移可结合函数图象、几何图形进行设问.1.平移前后,几何图形的形状、大小不发生变化,即平移前后两图形是全等的,可利用全等三角形的性质解题;2.平移后,可得到互相平行的对应线段,故可结合平行线的性质进行解题;3.在平移函数图象的过程中,图象上所有点的平移方式是相同的,可据此求函数解析式.
例3[2020湖北孝感]如图,点E在正方形ABCD的边CD上, 将△ADE绕点A顺时针旋转90°到△ABF的位置,连接 EF,过点A作EF的垂线,垂足为点H,与BC交于点G.若 BG=3,CG=2,则CE的长为 (　　)
【思路分析】　第一步,求AB,BC的长;第二步,设DE=x,用含x的代数式表示出CF,CE的长;第三步,证明△ABG∽△FCE,列比例式求解即可.
例4[2020安庆模拟]如图,在平面直角坐标系中,给出了 格点三角形ABC(顶点是网格线的交点),已知点B的 坐标为(1,2).(1)画出△ABC关于y轴对称的△A1B1C1,并写出点B1的坐标(点A,B,C的对应点分别为点A1,B1,C1);(2)在给定的网格中,以点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,画出△A2B2C2,并写出点B2的坐标(点A1,B1,C1的对应点分别为点A2,B2,C2).
常见的图形变换作图步骤1.对称作图(1)找出原图形的关键点;(2)作出关键点的对称点(关于x轴对称,横坐标相等,纵坐标互为相反数;关于y轴对称,纵坐标相等,横坐标互为相反数.关于一点对称,则关键点与其对应点的横坐标之和、纵坐标之和分别为对称中心的横、纵坐标的2倍);(3)按照原图形顺次连接得到的各对称点,得到原图形的对称图形.2.平移作图(1)确定平移的方向和平移的距离;(2)找出原图形的关键点,确定平移后的各对应点,其中横坐标左减右加,纵坐标上加下减;(3)按照原图形顺次连接得到的各对应点,即可得到平移后的图形.
3.旋转作图(1)确定旋转方向、旋转中心及旋转角度;(2)找出原图形的关键点;(3)确定旋转后的各对应点;(4)按照原图形顺次连接得到的各对应点,即可得到旋转后的图形.4.位似作图(1)确定位似中心;(2)确定原图形的关键点;(3)确定位似比,即要将图形放大或缩小的倍数;(4)确定各对应点;(5)按照原图形顺次连接得到的各对应点,即可得到所求位似图形.
例5[2020阜阳颍州区模拟]如图,在边长为1个单位长度 的小正方形组成的13×12的网格中,给出了以格点 (网格线的交点)为端点的线段AB.(1)将线段AB向上平移5个单位长度,得到线段A1B1(点A,B的对应点分别为点A1,B1),画出线段A1B1;连接AA1,BB1,并直接判断四边形ABB1A1的形状.(2)以点B为旋转中心,将线段BA顺时针旋转90°得到线段BC,画出线段BC,并直接写出 的长.
网格作图中常见的计算及其解题方法1.求角度及三角函数值 构造直角三角形或将要求的角进行等量代换,通常需要用到勾股定理.2.求通过旋转形成的图形的路径长(或周长)或面积(1)计算在旋转过程中某点经过的路径长:实质上是求旋转中心与该点的连线在旋转过程中形成的 扇形的弧长.首先确定旋转中心,再确定该点与旋转中心的距离,结合旋转角度,利用弧长公式 计算即可.(2)计算在旋转过程中某线段扫过的面积:先确定旋转中心及该线段的长度,再结合旋转角度,利用 扇形面积公式计算即可.3.求线段长的和的最小值及相关点坐标 一般为“将军饮马”问题,可通过对称作图进行解答.
利用对称解决与线段长有关的最值问题
例1 如图,在平面直角坐标系中,∠AOB的边OB与x轴正 半轴重合,点P是OA上的一动点,点N(3,0)在OB上, 点M是ON的中点,若∠AOB=30°,要使PM+PN的值最 小,则点P的坐标为　　　　.
【思路分析】　点M,N为两个定点(两定),点P为动点(一动),利用“模型1”即可求解.
例2 如图,在△ABC中,AB=AC=4,∠BAC=120°,P为AB上一动点,Q是BC上一动点,则AQ+PQ的最小值为(　　)
【思路分析】　点A为定点(一定),点P,Q分别为AB,BC上的动点(两动),根据“模型2”即可找到使得AQ+PQ的值最小的点P,Q,据此计算即可.
例3 [2020湖南永州]∠AOB在平面直角坐标系中的位 置如图所示,且∠AOB=60°,在∠AOB内有一点 P(4,3),点M,N分别是OA,OB上的动点,连接 PM,PN,MN,则△PMN周长的最小值是　　　　.
【思路分析】　点P为∠AOB内一点(一定),点M,N分别是OA,OB上的动点(两动),根据“模型3”即可找到△PMN的周长最小时点M,N的位置,再利用对称的性质、勾股定理等求解即可.