河南省南阳市南召县2022年九年级上学期期末数学试卷及答案

这是一份河南省南阳市南召县2022年九年级上学期期末数学试卷及答案，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
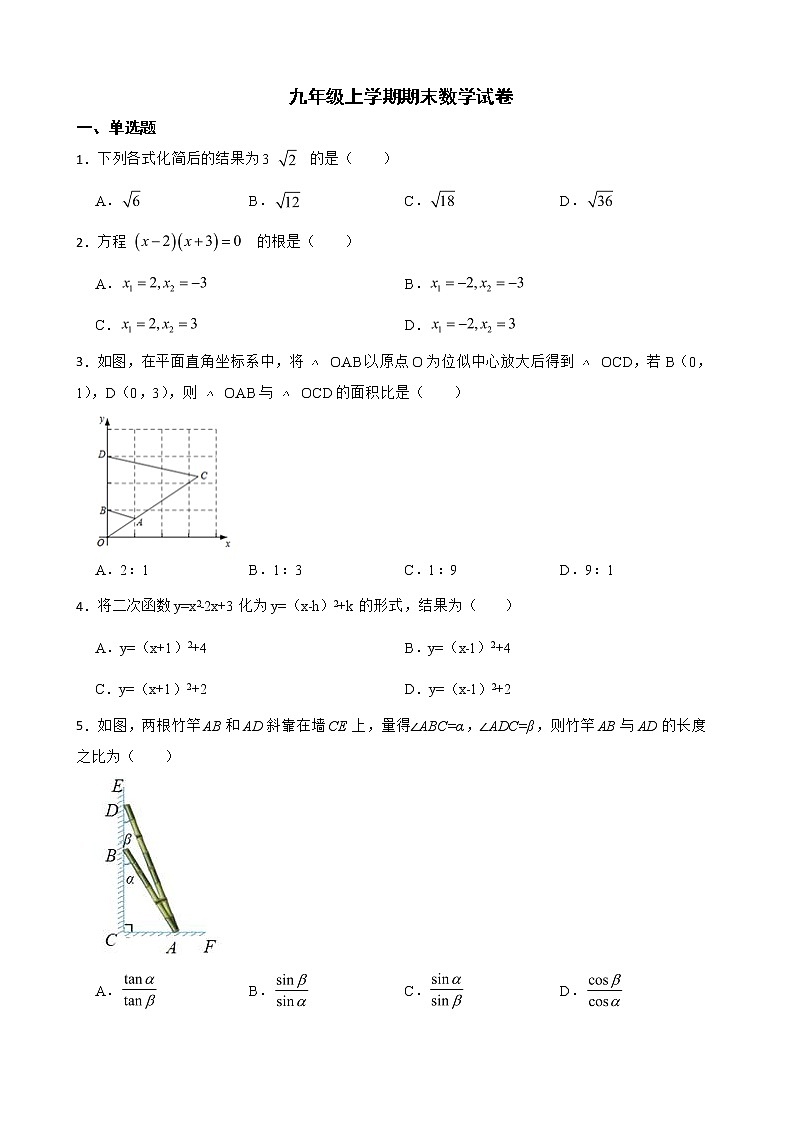
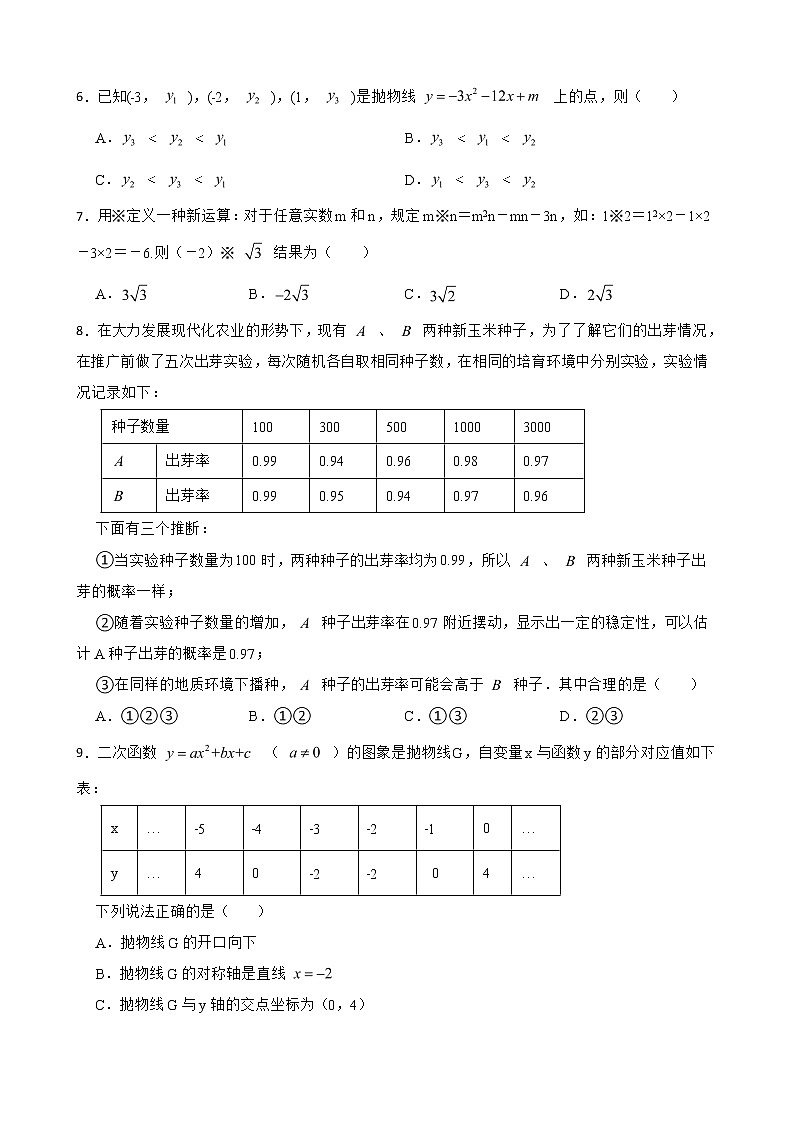
 九年级上学期期末数学试卷一、单选题1．下列各式化简后的结果为3 的是（　　）  A． B． C． D．2．方程 的根是（　　）   A． B．C． D．3．如图，在平面直角坐标系中，将 OAB以原点O为位似中心放大后得到 OCD，若B（0，1），D（0，3），则 OAB与 OCD的面积比是（　　）  A．2：1 B．1：3 C．1：9 D．9：14．将二次函数y=x2﹣2x+3化为y=（x﹣h）2+k的形式，结果为（　　）  A．y=（x+1）2+4 B．y=（x﹣1）2+4C．y=（x+1）2+2 D．y=（x﹣1）2+25．如图，两根竹竿AB和AD斜靠在墙CE上，量得∠ABC=α，∠ADC=β，则竹竿AB与AD的长度之比为（　　）A． B． C． D．6．已知(﹣3， )，(﹣2， )，(1， )是抛物线 上的点，则（　　）A．  B． C．  D． 7．用※定义一种新运算：对于任意实数m和n，规定m※n＝m2n－mn－3n，如：1※2＝12×2－1×2－3×2＝－6.则（－2）※ 结果为（　　）  A． B． C． D．8．在大力发展现代化农业的形势下，现有 、 两种新玉米种子，为了了解它们的出芽情况，在推广前做了五次出芽实验，每次随机各自取相同种子数，在相同的培育环境中分别实验，实验情况记录如下：  种子数量10030050010003000出芽率0.990.940.960.980.97出芽率0.990.950.940.970.96下面有三个推断：①当实验种子数量为100时，两种种子的出芽率均为0.99，所以 、 两种新玉米种子出芽的概率一样；②随着实验种子数量的增加， 种子出芽率在0.97附近摆动，显示出一定的稳定性，可以估计A种子出芽的概率是0.97；③在同样的地质环境下播种， 种子的出芽率可能会高于 种子．其中合理的是（　　）A．①②③ B．①② C．①③ D．②③9．二次函数 （ ）的图象是抛物线G，自变量x与函数y的部分对应值如下表：  x…﹣5﹣4﹣3﹣2﹣10…y…40﹣2﹣2 04…下列说法正确的是（　　）A．抛物线G的开口向下B．抛物线G的对称轴是直线 C．抛物线G与y轴的交点坐标为（0，4）D．当x＞﹣3时，y随x的增大而增大10．如图，已知菱形OABC的顶点O（0，0），B（2，2），菱形的对角线的交于点D；若将菱形OABC绕点O逆时针旋转，每秒旋转45°，从如图所示位置起，经过60秒时，菱形的对角线的交点D的坐标为（　　）A．（1，1） B．（﹣1，﹣1）C．（-1，1） D．（1，﹣1）二、填空题11．林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：移植的棵数n10001500250040008000150002000030000成活的棵数m8651356222035007056131701758026430成活的频率 0.8650.9040.8880.8750.8820.8780.8790.881估计该种幼树在此条件下移植成活的概率为　     　．12．如图，为了测量操场上一棵大树的高度，小英拿来一面镜子，平放在离树根部5m的地面上，然后她沿着树根和镜子所在的直线后退，当她后退1m时，正好在镜中看见树的顶端．小英估计自己的眼睛到地面的距离为1.6m，则大树的高度是　     　m．13．在平面直角坐标系 中，过点P（0，2）作直线 （b为常数且b<2）的垂线，垂足为点 ，则sin∠OPQ=　     　.  14．如图，已知函数 与 的图象交于点 ，点 的纵坐标为1，则关于 的方程 的解为　     　.  15．点P（m，n）在以y轴为对称轴的二次函数y=x2+ax+4的图象上，则m-n的最大值为　     　.三、解答题16．    （1）计算：4sin30°﹣ cos45°﹣ tan30°+2sin60°  （2）计算： 17．关于 的一元二次方程 ．  （1）若方程有两个相等的实数根用含 的代数式表示 ；  （2）若方程有两个不相等的实数根，且 ．  ①求 的取值范围；②写出一个满足条件的 的值，并求此时方程的根．18．根据公安部交管局下发的通知，春节前开展一次“一带一盔”安全守护行动，其中要求骑行摩托车、电动车需要佩戴头盔，某日交警部门在某个十字路口共拦截了50名不带头盔的骑行者，根据年龄段和性别得到如下表的统计信息，根据表中信息回答下列问题：年龄x（岁）人数男性占比x＜20450%20≤x＜30m60%30≤x＜402560%40≤x＜50875%x≥503100%（1）统计表中m的值为　     　；（2）若要按照表格中各年龄段的人数来绘制扇形统计图，则年龄在“30≤x＜40”部分所对应扇形的圆心角的度数为　     　；（3）若从年龄在“x＜20”的4人中随机抽取2人参加交通安全知识学习，请用列表或画树状图的方法，求恰好抽到1名男性和1名女性的概率.19．如图，在 ABC中，点D，E分别在边AB，AC上，连接DE.  （1）若AD•AB＝AE•AC.求证： ADE∽ ACB；  （2）若AB=8，AC=6，AD=3，直接写出：当AE=　     　时， ADE与 ACB相似.  20．（材料阅读）2020年5月27日，2020珠峰高程测量登山队成功登顶珠穆朗玛峰，将用中国科技“定义”世界新高度，其基本原理之一是三角高程测量法，在山顶上立一个标杆，找到2个以上测量点，分段测量山的高度，再进行累加.因为地球面并不是水平的，光线在空气中会发生折射，所以当两个测量点的水平距离大于300m时，还要考虑球气差，球气差计算公式为 （其中d为两点间的水平距离，R为地球的半径，R取6400000m），即：山的海拔高度=测量点测得山的高度+测量点的海拔高度+球气差.  （问题解决）某校科技小组的同学参加了一项野外测量某座山的海拔高度活动.如图，点A，B的水平距离d=800m，测量仪AC=1.5m，觇标DE=2m，点E，D，B在垂直于地面的一条直线上，在测量点A处用测量仪测得山顶标杆顶端E的仰角为37°，测量点A处的海拔高度为1800m.（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）.请你计算该山的海拔高度（要计算球气差，结果精确到0.01m）.21．某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙，它由长方形和抛物线构成，长方形的长AD=4米，宽AB=3米，抛物线的最高点E到BC的距离为4米.（1）按如图①所示的直角坐标系，抛物线可以用 表示.直接写出抛物线的函数表达式　          　 .  （2）现将A型活动板房改造为B型活动板房.如图②，在抛物线与AD之间的区域内加装一扇长方形窗户FGMN，点G，M在AD上，点N，F在抛物线上，窗户每平方米的成本为50元.已知GM=2米，直接写出：每个B型活动板房的成本是　     　元.（每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本）（3）根据市场信息，这样的B型活动板房公司每月最多能生产 个，若以单价 元销售B型活动板房，每月能售出 个；若单价每降低 元，每月能多售出 个这样的B型活动板房.不考虑其他因素，公司将销售单价 （元）定为多少时，每月销售B型活动板房所获利润 （元）最大？最大利润是多少？  22．如图，已知抛物线 经过 ABC的三个顶点，其中点A（0，1），点B（-9，10）， 轴，点P是直线AC下方抛物线上的动点.  （1）直接写出：b=　     　 ，c=　     　；（2）过点P且与y轴平行的直线l与直线AB，AC分别交于点E，F，当四边形AECP的面积最大时，求点P的坐标；（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C，P，Q为顶点的三角形与 ABC相似，若存在，直接写出点Q的坐标，若不存在，请说明理由.  23．如图，在 中，点 为斜边 上一动点，将 沿直线 折叠，使得点 的对应点为 ，连接 ， ， ， .  （1）如图①，若 ，证明： .  （2）如图②，若 ， ，求 的值.  （3）如图③，若 ，是否存在点 ，使得 .若存在，求此时 的值；若不存在，请说明理由. 
答案解析部分1．【答案】C2．【答案】A3．【答案】C4．【答案】D5．【答案】B6．【答案】B7．【答案】A8．【答案】D9．【答案】C10．【答案】B11．【答案】0.88012．【答案】813．【答案】14．【答案】15．【答案】16．【答案】（1）解：原式＝4× ﹣ × ﹣ × +2× ＝2﹣1﹣1+ ＝ （2）解：原式= = = = = 17．【答案】（1）解：∵关于 的一元二次方程 有两个相等的实数根，  ∴ ，∴ ．（2）解：①∵方程有两个不相等的实数根，且 ，  ∴ ，解得 ；②∵ ，∴ 可以是3此时方程为 ， ，解得 ， ．18．【答案】（1）10（2）180°（3）解：设两名男性用  表示，两名女性用  表示，根据题意，列表如下，   　 　                             　                             　                             　由上表可知，共有12种等可能的结果，符合条件的结果有8种，故P(恰好抽到1名男性和1名女性)=   19．【答案】（1）证明：∵AD⋅AB＝AE⋅AC， ∴又∵∠A＝∠A， ∴△ADE∽△ACB（2） 或420．【答案】解：如图，过点 作 于点 由题意，得 ， ， 在 中， ， 又 ，由题意，得 ， 故山的海拔高度为   21．【答案】（1）（2）500（3）解：根据题意，得 ， 每月最多能生产 个B型活动板房， ，解得 ， ， 时， 随 的增大而减小， 当 时， 有最大值，且最大值为 答：公司将销售单价 定为 元时，每月销售B型活动板房所获利润 最大，最大利润是 元.22．【答案】（1）2；1（2）解：因为 轴， .  所以 ，所以 ， ，所以点 的坐标 ， 因为点 ， ，所以直线 的解析式为 ，设点 所以 ，所以 ，因为 ， ，所以 因为 ，所以当 时，四边形 的面积的最大值是 ，此时点 （3）存在，Q（-4，1）或（3，1） 23．【答案】（1）证明： ， ，  ， ，由折叠的性质得： ， ， ， 四边形 是平行四边形，又 ， 平行四边形 是菱形，（2）解：如图，设 与 的交点为点 ，过点 作 于点 ，  ， 是等腰三角形， ，设 ，则 ， ， ，由折叠的性质得： ，在 和 中， ， ， ，设 ，则 ， ，解得 ， ，在 中， ， ，则 （3）解： ，  ，设 ，则 ，由折叠的性质得： ， ，由题意，分以下两种情况：①如图，当点 在直线 的左侧时，过点 作 于点 ， （等腰三角形的三线合一）， ， 在 中， ， ，又 ， ， ， ， 是等边三角形， ， ；②如图，当点 在直线 的右侧时，过点 作 于点 ，同理可得： ， ， 点 在 上，由折叠的性质得： ，在 中， ， ， ，综上，存在点 ，使得 ，此时 的值为 或