江苏南京市六合区2022_2023学年上学期九年级期中数学试题(含答案)

这是一份江苏南京市六合区2022_2023学年上学期九年级期中数学试题(含答案)，共12页。试卷主要包含了本试卷共8页，方程x2＝x的根为　▲　.等内容，欢迎下载使用。

2022～2023学年度第一学期期中学情分析样题
九年级数学
注意事项：
1．本试卷共8页．全卷满分120分．考试时间为120分钟．考生答题全部答在答题卡上，答在本试卷上无效．
2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．
3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效．
4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．
一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．下列方程中，关于x的一元二次方程的是
A．2x＝7
B．x2＋y＝5
C．x＝＋1
D．x2＋x＝4
2．若关于x的方程x2－mx＋2＝0有一个根是1，则m的值为
A．3
B．2
C．1
D．－3
3．用配方法解方程x2－4x＋3＝0，下列变形正确的是
A．(x－2)2＝－7
B．(x＋2)2＝1
C．(x＋2)2＝－1
D．(x－2)2＝1
4．如图，在△ABC中，∠C＝90°，∠B＝25°．若以点C为圆心，CA长为半径的圆与AB交于点D，则的度数为
B
A
C
D
（第4题）
A．25°
B．50°
A
B
C
O
C．60°
D．65°
A
B
D
C
（第5题）




（第6题）

5．如图，C是的中点，弦AB＝8，CD⊥AB，且CD＝2，则所在圆的半径为
A．4
B．5
C．6
D．10
6．如图，点A，B，C在⊙O上，∠AOC＝90°，AB＝，BC＝1，则⊙O的半径为
A．
B．
C．
D．
二、填空题（本大题共10小题，每小题2分，共20分．请把答案填写在答题卡相应位置上）
7．方程x2＝x的根为　▲　.
8．已知⊙O的半径为6cm，线段OP的长为4cm，则点P在⊙O　▲　(填“内”、“外”或“上”）.
9．若关于x的方程x2－2x＋m＝0没有实数根，则m的值可以是　▲　 (写出一个符合条件的值即可）.
A
B
C
O
（第16题）
O
A
B
D
C
（第10题）
（第11题）
C
A
P
B
O
10．如图，AB是⊙O的直径，弦CD∥AB．若∠B＝65°，则∠ADC＝　▲　°．






11．如图，AC，BC是⊙O的弦，PA，PB是⊙O的切线．若∠C＝50°，则∠P＝　▲　°．
12．某口罩厂六月份的口罩产量为100万只，由于市场需求量减少，八月份的产量减少到64万只．设七、八月份口罩产量的月平均减少率为x，则可列方程为 ▲ ．
13．已知a，b是方程x2＋x－3＝0的两个根，则ab－2022a－2022b的值是　▲　．
14．用半径为30cm，圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面，则这个圆锥底面圆的半径为　▲　cm．
15．若关于x的一元二次方程a(x＋h)2＋k＝0的两根分别为－3、2，则方程a(x－1＋h)2＋k＝0的根为 ▲ ．
16．如图，AB是⊙O的一条弦，点C在⊙O内，∠ACB＝90°，∠ABC＝30°，连接OC，若
⊙O的半径是4，则OC长的最小值为 ▲ ．
三、解答题（本大题共11小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（8分）解方程：
（1）x2－2x－1＝0； （2）(x＋1)＝3x＋3．


18．（8分）关于x的方程2x2＋(m＋2)x＋m＝0．
（1）求证：不论m取何值，方程总有两个实数根；
（2）若方程有两个相等的实数根，请求出m的值并求此时方程的根．


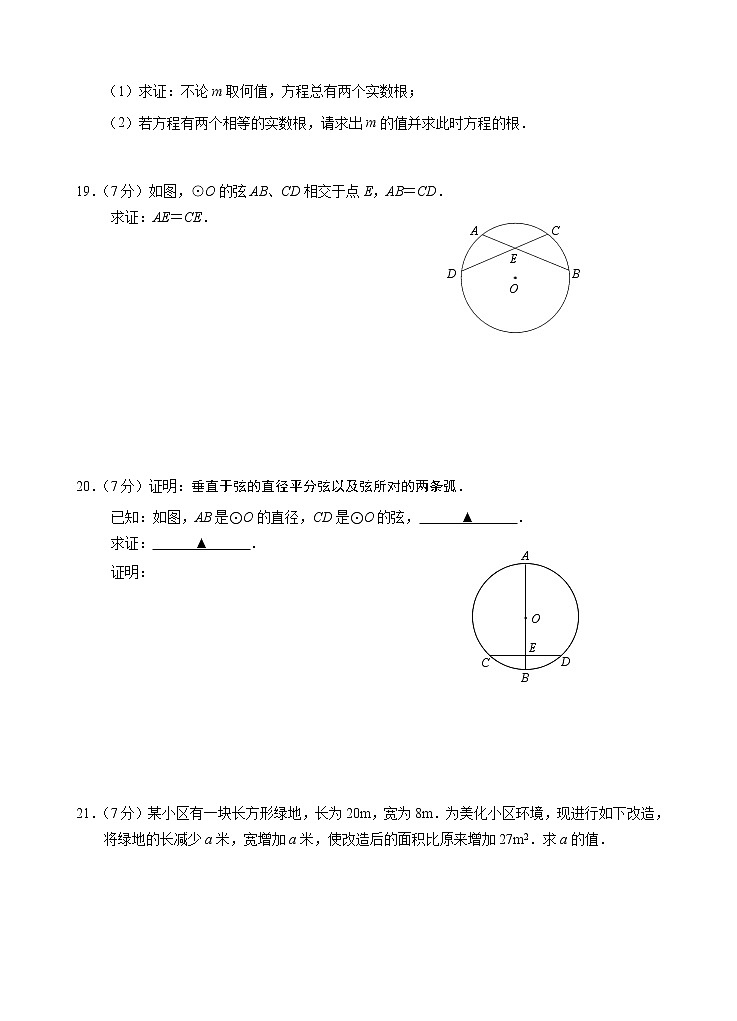
19．（7分）如图，⊙O的弦AB、CD相交于点E，AB＝CD．
A
D
E
C
B
O
求证：AE＝CE．








20．（7分）证明：垂直于弦的直径平分弦以及弦所对的两条弧．
已知：如图，AB是⊙O的直径，CD是⊙O的弦，　 ▲ 　．
D
E
C
A
B
O


求证：　 ▲ 　．
证明：








21．（7分）某小区有一块长方形绿地，长为20m，宽为8m．为美化小区环境，现进行如下改造，将绿地的长减少a米，宽增加a米，使改造后的面积比原来增加27m2．求a的值．







22.（7分）如图，在△ABC中，∠ACB＝90°，⊙O与AB相切，且与BC相切于点C．
（1）用直尺与圆规作出⊙OA
B
C


（不写作法，保留作图痕迹）；
（2）若AC＝3，BC＝4，则⊙O的半径为 ▲ ．







23．（7分）如图，在△ABC中，AE平分∠BAC，BE平分∠ABC，AE的延长线交△ABC的外接圆于点D，连接BD．
A
B
C
E
D
求证：DB＝DE．










24．（8分）如果关于x的一元二次方程ax2＋bx＋c＝0有两个实数根，且其中一个根是另一个根的3倍，那么称这样的方程为“三倍根方程”．例如，方程x2－4x＋3＝0的两个根是1和3，则这个方程就是“三倍根方程”．
（1）下列方程是三倍根方程的是 ▲ ；
①x2－3x＋2＝0 ②x2－3x＝0 ③x2－8x＋12＝0
（2）若关于x的方程x2－6x＋c＝0是“三倍根方程”，则c＝ ▲ ；
（3）若x2－(m＋n)x＋mn＝0是关于x的“三倍根方程”，求代数式的值．



25．（9分）某商场销售一批球鞋，其进价为每双200元．经市场调查发现，按每双300元出售，平均每天可售出20双. 假设球鞋的单价每降5元，商场平均每天可多售出10双. 该商场若想平均每天盈利4800元，则每双球鞋的定价为多少元？














D
O
C
E
B
A


26．（9分）在四边形ABCD中，∠C＝90°，E是BC上一点，以AE为直径的⊙O经过B，D两点，＝．
（1）求证：CD是⊙O的切线；
（2）若AD＝12，BE＝2，求AE的长．

















27. （11分）
为了解决一些较为复杂的数学问题，我们常常采用从特殊到一般的思想，先从特殊的情形入手，从中找到解决问题的方法．
已知四边形ABCD是⊙O的内接四边形，对角线AC与BD相交于点E．
【特殊情形】
E
O
A
C
D
B
①
F
（1）如图①，AC⊥BD，过圆心O作OF⊥AD，垂足为F．当BD是⊙O的直径时，求证：OF＝BC．





【一般情形】
E
O
A
C
D
B
②
F
（2）如图②，AC⊥BD，过圆心O作OF⊥AD，垂足为F．当BD不是⊙O的直径时，求证：OF＝BC．





【经验迁移】
A
B
C
D
F
M
E
O
③
（3）如图③，∠AED＝60°，AD＝12， F为上的一点，AF＝BC，若M为DF的中点，连接AM，则AM长的最小值为 ▲ ．





2022～2023学年度第一学期期中学情分析样题
九年级数学数学试卷参考答案及评分标准
说明：本评分标准每题给出了一种或几种解法供参考．如果考生的解法与本解答不同，参照本评分标准的精神给分．
一、选择题（本大题共6小题，每小题2分，共12分）
题号
1
2
3
4
5
6
答案
D
A
D
B
B
C



二、填空题（每小题2分，共20分，
7．x1＝0，x2＝1
8．内
9．答案不唯一，m大于1即可
10．25
11．80
12．100(1－x)2＝64
13．2019
14．10
15．x1＝－2，x2＝3
16．2－2．
三、解答题（本大题共11小题，共88分）
17．（8分）
（1）解：x2－2x＝1，
x2－2x＋1＝2 …………………………………………………………1分
（x－1）2＝2 …………………………………………………………2分
x－1＝± …………………………………………………………3分
∴x1＝1＋，x2＝1－．……………………………………………4分
（2）解：（x＋1）2－3（x＋1）＝0………………………………………………5分
（x＋1）（x＋1－3）＝0…………………………………………………6分
x＋1＝0或x＋1－3＝0． ………………………………………………7分
∴x1＝－1，x2＝2． ……………………………………………………8分
18．（8分）
（1）证明：b2－4ac＝（m＋2）2－4×2×m＝（m－2）2，……………2分
∵无论m取何值时，（m－2）2≥0，……………………………………3分
∴原方程总有两个实数根．………………………………………………4分
（2） 解：∵原方程有两个相等的实数根，
∴（m－2）2＝0，…………………………………………5分
解得m1＝m 2＝2，…………………………………………6分
将m＝2代入原方程得2x2＋4x＋2＝0…………………………………7分
∴原方程的根为：x1＝x2＝－1．………………………………………8分
19．（7分）证明：连接AC，AD，BC
∵AB＝CD，
D
B
A
O
C
E
∴＝．………………………………………2分
∴－＝－，即＝．…………4分
∴∠ACE＝∠CAE．………………………………6分
（第19题）
∴AE＝CE．………………………………………7分
20．（7分）
AB⊥CD，垂足为D ……………………………………………1分
D
E
C
A
B
O
（第20题）

求证：CE＝DE，＝，＝．…………2分
证明：连接OC、OD，…………3分
在△OCD中，∵OC＝OD，AB⊥CD，…………4分
∴CE＝DE，∠BOD＝∠BOC，…………………5分
∴∠AOD＝∠AOC…………………………………6分
∴＝，＝．…………………………7分
21．（7分）
解：由题意得，（20－a）（8＋a）－20×8＝27………………………………3分
整理，得a2－12a＋27＝0， ………………………………4分
解得a1＝3，a2＝9．………………………………………………………6分
答：a的值为3或9． …………………………………………………………7分A
B
C
（第22题）

O

22．（7分）
（1）如图所示，⊙O即为所求．………………………………5分


（2）．………………………………7分
23．（7分）

A
B
C
E
D
证明：∵ AE平分∠BAC，BE平分∠ABC，
∴∠ABE＝∠CBE，∠BAE＝∠CAD．………………1分
∴和所对的圆心角相等. ………………2分
∴＝． …………………………………………3分
∴∠DBC＝∠CAD． ………………4分
∴∠DBC＝∠BAE．
∵ ∠DBE＝∠CBE＋∠DBC，∠DEB＝∠ABE＋∠BAE，………………5分
∴ ∠DBE＝∠DEB． …………………………………6分
∴ DE＝DB． ……………………………………7分

24．（8分）
解：（1）③…………………………………………………………………………2分
（2）c＝．…………………………………………………………………4分
（3）设一个根为a，则另一个根为3a，
所以m＋n＝4a，mn＝3a2 ………………………………6分
＝＝＝ ………………………………8分

25．（9分）解：设每双球鞋降价x元，
由题意，得（300－x－200）（20＋×10）＝4800；……………5分
整理，得x2－90x＋1400＝0， …………………………………6分
解得x1＝20，x2＝70． …………………………………8分
所以定价为300－20＝280（元）
300－70＝230（元）…………………………………9分
答：每双球鞋定价为230或280元．
26．（9分）
D
O
C
E
B
A
（第26题）

F
（1）证明：连接DO并延长交AB于点F，连接OB、BD．
∵＝，
∴AD＝BD …………………………1分
又OA＝OB，
∴O、D都在AB的垂直平分线上．
∴DO是AB垂直平分线．…………………………2分
∴∠OFB＝90°，AF＝BF．
∵AE为⊙O的直径，
∴∠ABE＝90°．……………………………………………………………………3分
又∠C＝90°，
∴四边形BCDF是矩形．
∴OD⊥CD． ……………………………………………………………………4分
又∵点D在⊙O上，
∴CD是⊙O的切线．………………………………………………………………5分
（2）解：∵AO＝OE，AF＝BF ，
∴OF是△AEB的中位线，
∴OF＝BE＝1． …………………………6分
设⊙O的半径为r，在Rt△DAF中，AF2＝AD2－DF2＝122－(r＋1)2 ；
在Rt△OAF中，AF2＝OA2－OF2＝r2－12 ；
∴ 122－(r＋1)2＝r2－12 …………………………8分
解得 r1＝8，r 2＝－9 (舍去)．
∴ AE＝2r＝16． …………………………9分
27．（11分）
（1）证明：
E
O
A
C
D
B
②
F
∵在⊙O中，OF⊥AD，
∴DF＝AF．………………………………1分
又DO＝OB，
∴OF是△ADB的中位线，
∴OF＝AB．……………………………2分
∵BD为⊙O的直径，BD⊥AC，
∵＝，
∴AB＝BC．……………………………3分
∴OF＝BC．……………………………4分
E
O
A
C
D
B
③

F
G
（2）证明：作直径DG，连接AG．
∵在⊙O中，OF⊥AD，
∴DF＝AF．
又DO＝OG，
∴OF是△ADG的中位线，
∴AG＝2OF………………………………5分
∵＝，
∴∠G＝∠ACD．
∵DG是⊙O的直径，
∴∠DAG＝90°．
又AC⊥BD，∠DAG＋∠ADG＋∠AGD＝∠DEC＋∠EDC＋∠ACD＝180°，
∴∠ADG＝∠EDC．……………………6分
∴和所对的圆心角相等．
∴AG＝BC． ……………………7分
∴BC＝2OF，即OF＝BC．…………8分
（3）3．………………………………11分