2022-2023学年浙江省杭州地区（含周边）重点中学高一上学期期中考试数学

这是一份2022-2023学年浙江省杭州地区（含周边）重点中学高一上学期期中考试数学，共13页。试卷主要包含了考试结束后，只需上交答题卷，我国著名数学家华罗庚曾说，设函数，若，则的值为，已知，，，则下列结论正确的是等内容，欢迎下载使用。
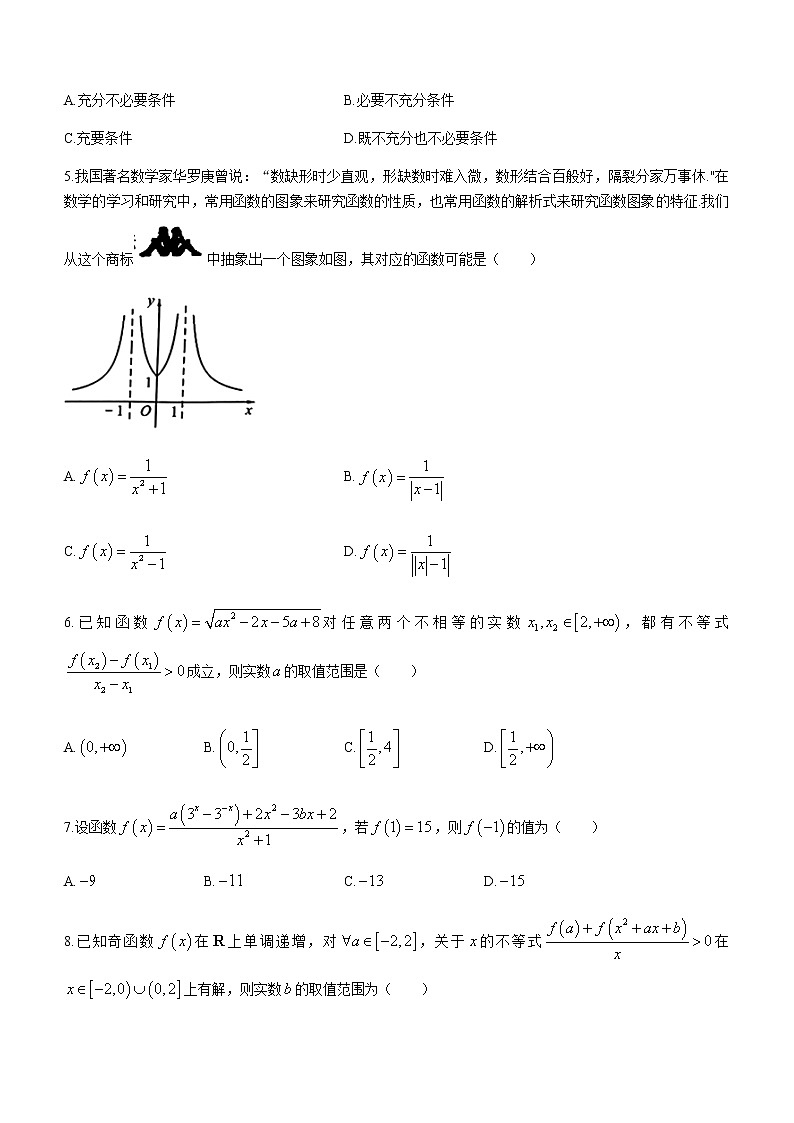
2022-2023学年浙江省杭州地区（含周边）重点中学高一上学期期中考试 数学 考生须知：1.本卷满分150分，考试时间120分钟；2.答题前，在答题卷密封区内填写班级、考试号和姓名；3.所有答案必须写在答题卷上，写在试卷上无效；4.考试结束后，只需上交答题卷。选择题部分一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。1.已知集合，，，则（    ）A. B. C. D.2.命题“，”的否定是（    ）A.，  B.，C.，  D.，3.下列函数与是同一个函数的是（    ）A.  B.C.  D.4.若，则“”是“”的（    ）A.充分不必要条件  B.必要不充分条件C.充要条件  D.既不充分也不必要条件5.我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休."在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来研究函数图象的特征.我们从这个商标中抽象出一个图象如图，其对应的函数可能是（    ）A.  B.C.  D.6.已知函数对任意两个不相等的实数，都有不等式成立，则实数的取值范围是（    ）A. B. C. D.7.设函数，若，则的值为（    ）A. B. C. D.8.已知奇函数在上单调递增，对，关于的不等式在上有解，则实数的取值范围为（    ）A.或  B.或C.  D.或二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，有选错的得0分，部分选对的得2分。9.若幂函数的图象过，下列说法正确的有（    ）A.且  B.是偶函数C.在定义域上是减函数 D.的值域为10.已知，，，则下列结论正确的是（    ）A. B. C. D.11.设，且，则下列结论正确的是（    ）A.的最小值为 B.的最大值为1C.的最小值为 D.的最大值为612.一般地，若函数的定义域为，值域为，则称为的“倍美好区间”。特别地，若函数的定义域为，值域也为，则称为的“完美区间”。下列结论正确的是（    ）A.若为的“完美区间”，则B.函数存在“完美区间”C.二次函数存在“2倍美好区间”D.函数存在“完美区间”，则实数的取值范围为非选择题部分三、填空题：本题共4小题，每小题5分，共20分。13.计算：______.14.秋冬季是流感的高发季节，为了预防流感，某学校决定用药熏消毒法对所有教室进行消毒。如图所示，已知药物释放过程中，室内空气中的含药量与时间（h）成正比；药物释放完毕后，与的函数关系式为（为常数），据测定，当空气中每立方米的含药量降低到0.25（）以下时，学生方可进教室，则学校应安排工作人员至少提前______小时进行消毒工作.15.已知定义在上的函数满足，若与的交点为，则______.16.若不等式对任意的恒成立，则的最大值为______.四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。17.（10分）已知（1）当时，求不等式的解集；（2）若命题：，使得为假命题。求实数的取值范围.18.（10分）已知全集为全体实数，集合，（1）在①，②，③这三个条件中选择一个合适的条件，使得，并求和；（2）若“”是“”的必要不充分条件，求实数的取值范围.19.（10分）已知定义在的奇函数，当时，.（1）求的值；（2）求在上的解析式；（3）若方程有且只有一个实数根，求实数的取值范围.20.（10分）截至2022年10月，杭州地铁运营线路共12条。杭州地铁经历了从无到有，从单线到多线，从点到面，从面到网，形成网格化运营，分担了公交客流，缓解了城市交通压力，激发出城市新活力。已知某条线路通车后，列车的发车时间间隔（单位：分钟）满足，经市场调研测算，列车的载客量与发车时间间隔相关，当时，列车为满载状态，载客量为600人，当时，载客量会减少，减少的人数与的平方成正比，且发车时间间隔为3分钟时的载客量为502人，记列车载客量为.（1）求的表达式，并求当发车时间间隔为5分钟时的载客量；（2）若该线路每分钟净收益为（单位：元），则当发车时间间隔为多少时，该线路每分钟的净收益最大，并求出最大值.21.（15分）已知函数（1）若为偶函数，求的值并证明函数在上的单调性；（2）在（1）的条件下，若函数在区间上的最小值为，求实数的值；（3）若为奇函数，不等式在上有解，求实数的取值范围.22.（15分）已知，（1）若在区间上不单调，求实数的取值范围；（2）若在区间上的最大值为，最小值为，且的最小值为1，求实数的值；（3）若对恒成立，求实数的取值范围.  2022学年第一学期期中杭州地区（含周边）重点中学高一年级数学学科参考答案 一、二、选择题123456789101112CABADCBAABACDACBCD三、填空题13．  14．1    15．10    16．四、解答题17．解：（1）当时，原不等式的解集为                ……………（占3分）（第（1）问共占3分）（2）∵命题：，使得为假命题∴：恒成立为真命题即：对恒成立            ………（占2分）①当即时，恒成立，∴符合题意； ………（占1分）②当即时∴    ………（占3分）综上所述：                         ………（占1分）（第（2）问共占7分，如果没写命题的否定直接讨论，答案对的也给7分）18．解：（1）由题知：集合，  ………………（占2分）∵，∴需选条件③                      ……………………（占1分）此时，    ………………（占2分）                                 ………………（占1分）（第（1）问共占6分）（2）∵“”是“”的必要不充分条件∴是的真子集     …………（占1分）∴                                   ………………（占2分）∴                 …………（占1分）（第（2）问共占4分） 19．解：（1）       ………………（占2分）（第（1）问共占2分）（2）（第（2）问共占4分，第一条式子不占分，第二条式子占1分，第三条式子占3分）（3）由图知：   ………………（占2分）∴     ………………（占2分）（第（3）问共占4分）20．解：（1）当时，当时，设而，∴∴    ………………（占3分）∴，即发车时间间隔为5分钟时的载客量为550人.  ………………（占1分）（第（1）问共占4分）（2）当时当且仅当，即时等号成立.     ………………（占4分）当时，单调递减，∴当时，取到最大为67.6（占1分）∵ 67.6<116∴当发车时间间隔为分钟时，该线路每分钟的净收益最大，最大值为116元（占1分）（第（2）问共占6分）21．解：（1）∵为偶函数，∴代入计算得： ∴  …（占2分）对，当时，∵       ∴∴∴函数在上单调递增       ………………（占3分）（第（1）问共占5分）（2）令   ∵  ∴∴   …………（占1分）①当时，  解得： ∴无解     ………（占2分）②当时，  解得：  ∵∴  …（占2分）综上所述：（第（2）问共占5分，答案不对有分类讨论思想酌情给分）（3）∵为奇函数，∴  ∴，   ………（占1分）又∵不等式在上有解∴∴由平方差和立方差公式得：  ………（占1分）令∵   ∴ ∴而在上单调递增，所以∴    ………（占3分）（第（3）问共占5分，用根的分布做答案对也给5分）22．解：（1）∵在区间上不单调，∴，∴   ………………（占3分）（第（1）问共占3分）（2）的对称轴为，要使达到最小，与必关于对称轴对称，∴     ①                                 …………（占2分），代入化简得：    ②   …………（占2分）由①②解得：        …………（占1分）（第（2）问共占5分，用分类讨论求最值能得出答案的也给5分）（3）法1：∵∴令∴           …………（占2分）而为偶函数，且在单调递增，∴对恒成立           …………（占2分）（这个式子不是同构得到而是代入化简得到的也给4分）∴法1：参变量分离得：令∵  ∴∴当时， 的最小值为同理：的最大值为   综上所述：      …………（占3分）（第（3）问共占7分）（3）法2：∵∴令∴           …………（占2分）而为偶函数，且在单调递增，∴对恒成立           …………（占2分）（这个式子不是同构得到而是代入化简得到的也给4分）∴∵  ∴对恒成立，令∴  解得：令当时， ∴当时， ∴无解当时， ∴         综上所述：   …………（占3分）（第（3）问共占7分）