初中数学人教版九年级上册24.4 弧长及扇形的面积同步练习题

这是一份初中数学人教版九年级上册24.4 弧长及扇形的面积同步练习题，共44页。试卷主要包含了米.，cm等内容，欢迎下载使用。
九年级上册数学24.4 弧长和扇形的面积 试题分类选编2附答案
1．（2022·山东烟台·九年级期末）如图，正方形的边长为4，以点为圆心，为半径画圆弧得到扇形（阴影部分，点在对角线上）．若扇形正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（    ）

A． B．1 C． D．
2．（2022·山东·烟台市福山区教学研究中心九年级期末）如图，公园内有一个半径为18米的圆形草坪，从地走到地有观赏路（劣弧）和便民路（线段）.已知、是圆上的点，为圆心，，小强从走到，走便民路比走观赏路少走（    ）米.

A． B．
C． D．
3．（2022·山东·济宁学院附属中学九年级期末）如图，面积为的正方形内接于⊙O，则的长度为（    ）

A． B． C． D．
4．（2022·山东临沂·九年级期末）如图，的内接正六边形的边长为，则的长为（    ）

A． B． C． D．
5．（2022·山东聊城·九年级期末）如图，四边形ABCD是半径为2的⊙O的内接四边形，连接OA，OC．若∠ADC＝72，则的长为（　　）

A． B． C． D．
6．（2022·山东泰安·九年级期末）一个几何体的三视图如下：其中主视图和左视图都是腰长为4，底边为2的等腰三角形，则这个几何体侧面展开图的面积和圆心角分别是（    ）


A．4π  60° B．4π  90° C．2π  90° D．8π  60°
7．（2022·山东德州·九年级期末）如图，从一张腰长为90cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面圆的半径为（　　）cm．


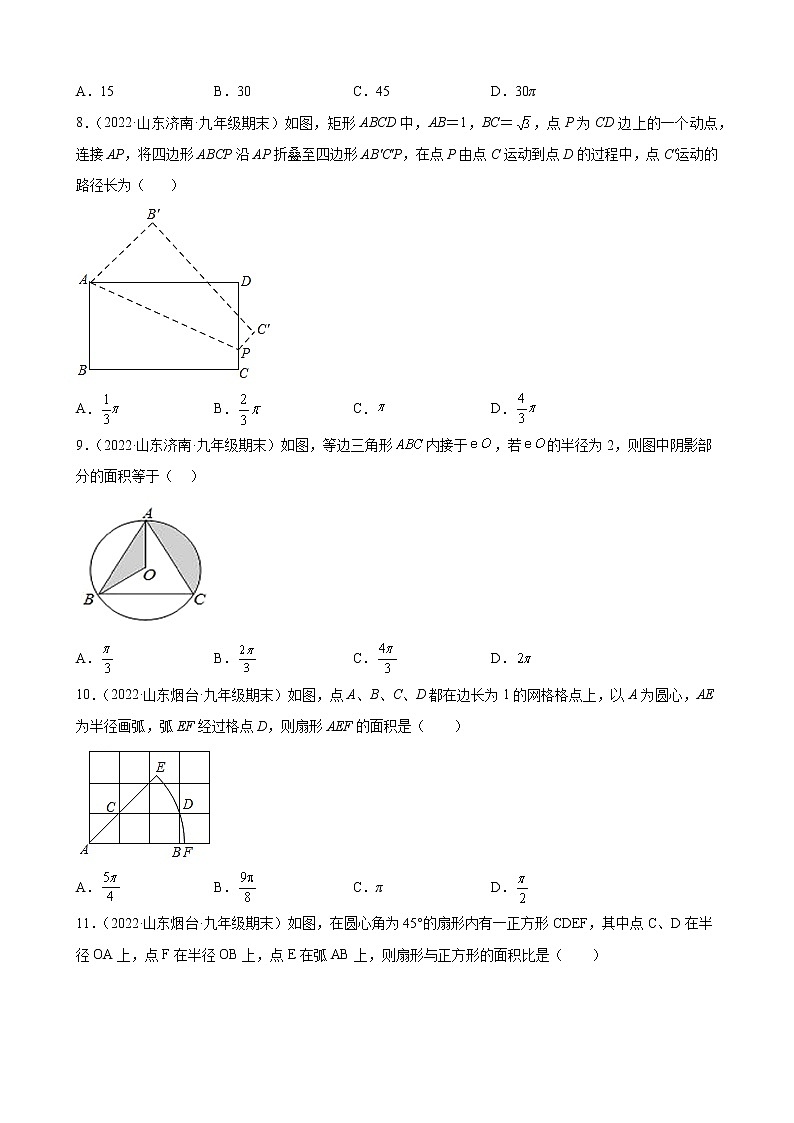
A．15 B．30 C．45 D．30π
8．（2022·山东济南·九年级期末）如图，矩形ABCD中，AB＝1，BC＝，点P为CD边上的一个动点，连接AP，将四边形ABCP沿AP折叠至四边形AB'C'P，在点P由点C运动到点D的过程中，点C'运动的路径长为（      ）

A． B． C． D．
9．（2022·山东济南·九年级期末）如图，等边三角形内接于，若的半径为2，则图中阴影部分的面积等于（    ）

A． B． C． D．
10．（2022·山东烟台·九年级期末）如图，点A、B、C、D都在边长为1的网格格点上，以A为圆心，AE为半径画弧，弧EF经过格点D，则扇形AEF的面积是（　　）

A． B． C．π D．
11．（2022·山东烟台·九年级期末）如图，在圆心角为45°的扇形内有一正方形CDEF，其中点C、D在半径OA上，点F在半径OB上，点E在弧AB上，则扇形与正方形的面积比是（　　）

A．π：8 B．5π：8 C．π：4 D．π：4
12．（2022·山东淄博·九年级期末）如图，以为直径，点为圆心的半圆经过点，若，则图中阴影部分的面积为（    ）

A． B． C． D．
13．（2022·山东德州·九年级期末）如图，四边形ABCD内接于圆O，对角线AC是圆O的直径，DB平分，AC长6cm，求阴影部分的面积（    ）

A． B． C． D．
14．（2022·山东泰安·九年级期末）如图，的内切圆与分别相切于点D，E，F，连接，，，，，则阴影部分的面积为（ ）

A． B． C． D．
15．（2022·山东济南·九年级期末）如图，正方形ABCD内接于圆O，AB＝4，则图中阴影部分的面积是（  ）

A． B． C． D．
16．（2022·山东烟台·九年级期末）如图，AB⊥OB，AB=2，OB=4，把∠ABO绕点O顺时针旋转60°得∠CDO，则AB扫过的面积（图中阴影部分）为（　　）

A．2 B．2π C．π D．π
17．（2022·山东临沂·九年级期末）如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是（    ）

A．3π B．6π C．5π D．4π
18．（2022·山东·济宁学院附属中学九年级期末）如图，正方形的边长为4，分别以正方形的三条边为直径在正方形内部作半圆，则阴影部分的面积是（    ）

A． B． C． D．
19．（2022·山东烟台·九年级期末）已知圆锥的底面半径为6，母线长为10，则这个圆锥的全面积为（    ）
A． B． C． D．
20．（2022·山东东营·九年级期末）用一个半径为面积为的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径为（  ）
A． B． C． D．
21．（2022·山东·武城县教育教学研究中心九年级期末）一个母线是6的圆锥侧面展开图的圆心角是120°，则圆锥的高是（    ）
A． B． C．4 D．8
22．（2022·山东日照·九年级期末）如图，圆锥体的高，底面圆半径，则该圆锥体的侧面展开图的圆心角的度数是（    ）

A．60° B．90° C．120° D．150°
23．（2022·山东聊城·九年级期末）如图，分别以等边三角形的每个顶点为圆心、以边长为半径，在另两个顶点间作一段圆弧，三段圆弧围成的曲边三角形称为勒洛三角形．若等边三角形的边长为，则勒洛三角形的周长为_____．

24．（2022·山东临沂·九年级期末）已知圆锥的底面半径为40cm， 母线长为90cm， 则它的侧面展开图的圆心角为_______．
25．（2022·山东临沂·九年级期末）如图，，以O为圆心，4为半径作弧交于点A，交于点B，分别以点A，B为圆心，大于的长为半径画弧，两弧在的内部相交于点C，画射线交于点D，E为上一动点，连接，，则阴影部分周长的最小值为_________．

26．（2022·山东德州·九年级期末）圆心角为，半径为2的扇形的弧长是_______.
27．（2022·山东菏泽·九年级期末）如图，将线段AB绕点A顺时针旋转30°，得到线段AC．若AB＝5，则点B经过的路径BC长度为____．（结果保留π）


28．（2022·山东德州·九年级期末）已知扇形的圆心角为120°，弧长为6π，则它的半径为________．
29．（2022·山东临沂·九年级期末）如图所示，在矩形纸片上剪下一个扇形和一个圆形，使之恰好能围成一个圆锥模型.若扇形的半径为R，圆的半径为r，则R与r满足的数量关系是 ___.

30．（2022·山东·烟台市福山区教学研究中心九年级期末）如图①是山东舰航徽的构图，采用航母45度破浪而出的角度，展现山东舰作为中国首艘国产舰母横空出世的气势，将舰徽中第一条波浪抽象成几何图形，则是一条长为的弧，若该弧所在的扇形是高为12的圆锥侧面展开图（如图②），则该圆锥的母线长为____________．

31．（2022·山东济宁·九年级期末）如图，在中，，，，将绕直角顶点顺时针旋转，当点的对应点落在边上时，停止转动，则点经过的路径长为__．

32．（2022·山东德州·九年级期末）如图，边长为的正六边形在足够长的桌面上滚动(没有滑动)一周，则它的中心点所经过的路径长为______．

33．（2022·山东临沂·九年级期末）如图，等腰直角三角形中，．分别以点B、点C为圆心，线段长的一半为半径作圆弧，交、、于点D、E、F，则图中阴影部分的面积为____．

34．（2022·山东滨州·九年级期末）如图，以A为圆心AB为半径作扇形ABC，线段AC交以AB为直径的半圆弧的中点D，若AB＝4，则阴影部分图形的面积是_______（结果保留π）．

35．（2022·山东德州·九年级期末）如图，边长为2的正方形ABCD内接于⊙O，点E是上一点（不与A、B重合），点F是上一点，连接OE，OF，分别与AB，BC交于点G，B，且∠EOF＝90°．有下列结论：①＝；②四边形OGBH的面积随着点E位置的变化而变化；③△GBH周长的最小值为2+；④若BG＝1﹣，则BG，GE，围成的面积是，其中正确的是_____．（把所有正确结论的序号都填上）

36．（2022·山东济南·九年级期末）如图，分别以等边三角形的3个顶点为圆心，边长为半径画弧，三段弧围成的图形称为菜洛三角形，若等边三角形边长为3cm，则该莱洛三角形的面积为________．

37．（2022·山东泰安·九年级期末）如图，是的直径，点在上，，，．若的半径为1，则图中阴影部分的面积是______（结果保留）．

38．（2022·山东泰安·九年级期末）如图，在扇形中，，点为的中点，交于点，以点为圆心，的长为半径作交于点．若，则图中阴影部分的面积为__________．

39．（2022·山东青岛·九年级期末）在△ABC中，已知∠ABC＝90°，∠BAC＝30°，BC＝1，如图所示，将△ABC绕点A按逆时针方向旋转90°后得到△AB′C′．则图中阴影部分的面积为_____．

40．（2022·山东烟台·九年级期末）如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交于点E，以点O为圆心，OC的长为半径作交OB于点D，若OA=2，则阴影部分的面积为 .

41．（2022·山东泰安·九年级期末）如图，AB是半圆O的直径，且AB=8，点C为半圆上的一点．将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是____．（结果保留π）

42．（2022·山东烟台·九年级期末）如图，在扇形OAB中，点C在 上，∠AOB＝90°，∠ABC＝30°，AD⊥BC于点D，连接AC，若OA＝4，则图中阴影部分的面积为 _____．

43．（2022·山东泰安·九年级期末）如图，四边形ABCD是矩形，AB＝2，AD＝，以点A为圆心，AB长为半径画弧，交CD于点E，交AD的延长线于点F，则图中阴影部分的面积是_____．

44．（2022·山东济南·九年级期末）如图，是的直径，弦，垂足为，，，则______．

45．（2022·山东济宁·九年级期末）一个圆锥的底面圆的半径为 2，母线长为 4，则它的侧面积为______．
46．（2022·山东东营·九年级期末）圆锥的侧面展开图的面积是15πcm2，母线长为5cm，则圆锥的底面半径长为_____cm．
47．（2022·山东·济宁学院附属中学九年级期末）如图，将半径为3cm的圆形纸片剪掉三分之一，余下部分围成一个圆锥的侧面，则这个圆锥的高是 cm．

48．（2022·山东烟台·九年级期末）如图，圆锥母线长BC＝18cm，若底面圆的半径OB＝4cm，则侧面展开扇形图的圆心角为______．

49．（2022·山东临沂·九年级期末）如图，在平面直角坐标系中，A(3，3)，B(4，0)，C(0，﹣1)．
（1）以点C为旋转中心，把ABC逆时针旋转90°，画出旋转后的图形C；
（2）在（1）的条件下，
①点A经过的路径的长为　 　（结果保留π）；
②则此时B'点的坐标为　 　．

50．（2022·山东济宁·九年级期末）如图，AB为⊙O的直径，射线AD交⊙O于点F，点C为劣弧的中点，CE为⊙O的切线交AD于点E，连接AC．
（1）求证：CE⊥AD；
（2）若∠BAC＝30°，AB＝4，求阴影部分的面积．


51．（2022·山东聊城·九年级期末）如图，为的直径，是上一点，过点的直线交的延长线于点，，垂足为，是与的交点，平分．

（1）求证：是的切线；
（2）若，，求图中阴影部分的面积．

52．（2022·山东·武城县教育教学研究中心九年级期末）如图，线段AB为⊙O的直径，点C、点D为半圆AB的三等分点，点F为线段AB延长线上一点，且OB=BF．

(1)求证：直线DF是⊙O的切线；
(2)⊙O的半径为2，求图中阴影部分的面积．




53．（2022·山东淄博·九年级期末）如图，已知扇形AOB的圆心角为120°，半径OA为9cm．

(1)求扇形AOB的弧长和扇形面积；
(2)若把扇形纸片AOB卷成一个圆锥形无底纸帽，求这个纸帽的高OH．

参考答案：
1．D
【解析】根据题意，扇形ADE中弧DE的长即为圆锥底面圆的周长，即通过计算弧DE的长，再结合圆的周长公式进行计算即可得解．
∵正方形的边长为4
∴
∵是正方形的对角线
∴
∴
∴圆锥底面周长为，解得
∴该圆锥的底面圆的半径是，
故选：D．
本题主要考查了扇形的弧长公式，圆的周长公式，正方形的性质以及圆锥的相关知识点，熟练掌握弧长公式及圆的周长公式是解决本题的关键．
2．D
【解析】作OC⊥AB于C，如图，根据垂径定理得到AC=BC，再利用等腰三角形的性质和三角形内角和计算出∠A，从而得到OC和AC，可得AB，然后利用弧长公式计算出的长，最后求它们的差即可．
解：作OC⊥AB于C，如图，
则AC=BC，
∵OA=OB，
∴∠A=∠B=（180°-∠AOB）=30°，
在Rt△AOC中，OC=OA=9，
AC=，
∴AB=2AC=，
又∵=，
∴走便民路比走观赏路少走米，
故选D．

本题考查了垂径定理：垂径定理和勾股定理相结合，构造直角三角形，可解决计算弦长、半径、弦心距等问题．
3．C
【解析】连接BD、AC，由题意易得，然后根据弧长计算公式可求解．
解：连接BD、AC，

∵四边形是正方形，且面积为18，
∴，
∴，
∴，
∴的长度为；
故选C．
本题主要考查弧长计算及正多边形与圆，熟练掌握弧长计算及正多边形与圆是解题的关键．
4．B
【解析】如图（见解析），先根据圆内接正六边形的性质求出中心角，再根据等边三角形的判定与性质可得，然后利用弧长公式即可得．
图，连接OB、OC，


由题意得：，
正六边形是的内接正六边形，
中心角，
又，
是等边三角形，
，
则的长为，
故选：B．
本题考查了圆内接正六边形的性质、弧长公式等知识点，熟练掌握圆内接正六边形的性质是解题关键．
5．D
【解析】利用圆周角与圆心角的关系求得∠AOC=144°，结合弧长公式进行解答即可．
解：∵四边形内接于⊙O，∠AOC=2∠ADC，
∴∠AOC=2×72°=144°，
∴的长=，
故选：D．
本题考查了圆周角定理、弧长的计算，本题中利用圆周角定理中圆周角与圆心角的关系得出角的度数，从而得到∠AOC=144°，从而得出的长．
6．B
【解析】由三视图先确定几何体为圆锥，利用圆锥侧面积公式计算，根据侧面展开图扇形弧长与底面圆周长列方程，解方程即可．
解：从三视图看几何体为圆锥，母线长为4，底面圆的半径为1，
∴圆锥侧面积为：，
∴，
∴圆心角为：．
故选择B．
本题考查三视图还原几何体，圆锥侧面面积与侧面展开图扇形圆心角，掌握三视图还原几何体的方法，熟记圆锥侧面积公式，弧长公式是解题关键．
7．A
【解析】作出等腰三角形底边上的高线OE，首先根据直角三角形30°所对的直角边等于斜边的一半求出等腰三角形底边上的高线OE的长度，即得到扇形OCD所在的圆的半径R，然后根据弧长公式求出的长度，的长度即为圆锥底面圆的周长，最后根据周长求出半径即可．
如图，过点O作OE⊥AB，垂足为E，
∵△OAB为顶角为120°的等腰三角形，
∴=30°，cm，
∴cm，
设圆锥的底面圆半径为rcm，根据题意得，
，
解得，
所以该圆锥的底面圆的半径为15cm，
故选A．

本题考查了直角三角形30°所对的直角边等于斜边的一半、扇形的弧长公式、圆的周长公式，准确将扇形的弧长转化为底面圆的周长是解决本题的关键．
8．B
【解析】根据题意判断出C'点的运动轨迹是以A点为圆心，AC'为半径的一段圆弧，得出圆心角即可计算．
解：连接AC和AC'，
由题知，AC'的长度保持不变，
∴C'点的运动轨迹是以A点为圆心，AC'为半径的一段圆弧，

∵AB=1，BC=，
∴AC==2，
∴∠ACB=∠CAD=30°，
当点P由运动到点D时，∠CAC'=60°，
即AC'的旋转角度为60°，
∴点C'运动的路径长为，
故选：B．
本题主要考查点运动的路径长，根据题意得出C'点的运动轨迹是解题的关键．
9．C
【解析】连接OC，如图，利用等边三角形的性质得，，然后根据扇形的面积公式，利用图中阴影部分的面积进行计算．
解：连接OC，如图，
为等边三角形，
，，
图中阴影部分的面积

故选C．
本题考查了三角形的外接圆与外心：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心也考查了等边三角形的性质．
10．A
【解析】根据题意以及网格的特点求得，圆弧的半径为，进而根据扇形面积公式进行计算即可．
依题意，点A、B、C、D都在边长为1的网格格点上，
,，
扇形AEF的面积．
故选A．
本题考查了网格的特点，勾股定理，扇形面积，根据网格的特点求得圆心角和半径是解题的关键．
11．B
【解析】连接OE，设正方形的边长为a．根据等腰直角三角形的性质，得OC=CF=a，在直角三角形OFC中，根据勾股定理列方程，用a表示出r的值，再根据扇形及正方形的面积公式求解．
解：连接OE，设正方形的边长为a，则正方形CDEF的面积是a2，

在Rt△OCF中，a2+（2a）2=r2，即r=a，
扇形与正方形的面积比=：a2=：a2=5π：8．
故选B．
本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．
12．A
【解析】先利用圆周角定理可得，然后可得△ABC是等腰直角三角形，进而可得△AOC和△BOC都为等腰直角三角形，于是得到，然后根据扇形面积公式可进行求解．
解：∵为直径，
∴，
∵，
∴△ABC是等腰直角三角形，
∴，则OA=OB=1，
∴OC⊥AB，
∴△AOC和△BOC都为等腰直角三角形，
∴，
∴；
故选A．
本题主要考查扇形面积公式及圆周角定理，熟练掌握扇形面积公式及圆周角定理是解题的关键．
13．A
【解析】连接OD，求出，求出扇形ODC的面积，的面积，两者相减即可求出阴影部分的面积．
解：连接OD，

∵直径AC长6cm，
∴半径为3cm，，
∵DB平分，
∴，
∴，
∴扇形ODC的面积为，
的面积为，
∴阴影部分的面积为，
故选：A．
本题考查求弓形的面积，扇形面积，圆周角定理，同弧所对的圆周角等于圆心角的一半，解题的关键是求出，扇形ODC的面积，的面积．
14．C
【解析】连接OD，由题意，先利用勾股定理求出AB的长度，设半径为r，然后求出内切圆的半径，再利用正方形的面积减去扇形的面积，即可得到答案．
解：连接OD，如图：

在中，，，，
由勾股定理，则
，
设半径为r，则，
∴，
∴四边形CEOF是正方形；
由切线长定理，则，，
∵，
∴，
解得：，
∴；
∴阴影部分的面积为：；
故选：C．
本题考查了三角形的内切圆，切线的性质，切线长定理，求扇形的面积，勾股定理等知识，解题的关键是熟练掌握所学的知识，正确的进行解题．
15．B
【解析】连接OA、OB，利用正方形的性质得出OA=ABcos45°=2，根据阴影部分的面积=S⊙O-S正方形ABCD列式计算可得．
解：连接OA、OB，

∵四边形ABCD是正方形，
∴∠AOB=90°，∠OAB=45°，
∴OA=ABcos45°=4×=2，
所以阴影部分的面积=S⊙O-S正方形ABCD=π×（2）2-4×4=8π-16．
故选B．
本题主要考查扇形的面积计算，解题的关键是熟练掌握正方形的性质和圆的面积公式．
16．C
【解析】根据勾股定理得到OA，然后根据边AB扫过的面积==解答即可得到结论．
如图，连接OA、OC．
∵AB⊥OB，AB=2，OB=4，∴OA==，∴边AB扫过的面积=== =．

故选C．
本题考查了扇形的面积的计算，勾股定理，熟练掌握扇形的面积公式是解题的关键．
17．B
阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积．
则阴影部分的面积是：=6π
故选：B．
18．D
【解析】根据S阴影=2×(S半圆-S△AOD)求解即可．
如图，连接OA、OD，
则根据对称性可得：S阴影=2×(S半圆-S△AOD)=，
故选：D．

本题考查扇形的面积计算，正方形的性质，解题关键是表示出两个弓形面积之和与半圆与三角形面积之间的关系．
19．D
【解析】首先求得底面周长，即展开得到的扇形的弧长，然后利用扇形面积公式及底面积计算公式求出圆锥的侧面积和底面积，再根据圆锥的全面积=圆锥的侧面积+圆锥的底面积即可求解．
解：∵底面周长是：2×6π＝12π，
则圆锥的侧面积是：×12π×10＝60π，
圆锥的底面积是：==36π，
∴圆锥的全面积=圆锥的侧面积+圆锥的底面积=60π+36π=96π．
故选：D．
本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．
20．D
【解析】根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到•2π•r•3=3π，然后解方程即可．
解：根据题意得•2π•r•3=3π，
解得r=1．
故选：D．
本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
21．B
【解析】圆锥的侧面展开图为扇形，母线即为该扇形的半径，在圆心角已知的情况下，可得该扇形的弧长，该弧长也是圆锥底面圆的周长，由此可得底面圆半径，底面圆半径、母线、圆锥的高在一个直角三角形中，根据勾股定理可求得答案．
设圆锥底面圆的半径为r，由题意可得，圆锥底面圆的周长2πr=，
解得：r=2


圆锥的高= ，
故选B．
本题考查圆锥的有关计算，准确理解各个量之间的关系是解题的关键．
22．C
【解析】根据勾股定理，可求出母线长为=3，圆锥的底面周长为2πr=2π，根据圆锥展开图弧长公式即可求出圆心角.
解：圆锥的底面周长为2πr=2π
由勾股定理，得圆锥的母线长为==3，
∵=2π
∴n=120
故选：C.
本题主要考查了圆锥侧面展开图求圆心角的问题，注意等量的转化，圆锥的底面圆周长=展开图扇形弧长，圆锥母线长=展开图扇形半径，同时注意母线长=，熟练地掌握以上知识是解决问题的关键.
23．πa
【解析】首先根据等边三角形的性质得出∠A=∠B=∠C=60°，AB=BC=CA=a，再利用弧长公式求出的长=的长=的长=，那么勒洛三角形的周长为
解：如图．∵△ABC是等边三角形，

∴∠A=∠B=∠C=60°，AB=BC=CA=a，
∴的长=的长=的长=，
∴勒洛三角形的周长为
故答案为：πa．
本题考查了弧长公式，解题的关键是掌握（弧长为l，圆心角度数为n，圆的半径为R），也考查了等边三角形的性质．
24．
【解析】圆锥的底面半径为40cm，则底面圆的周长是80πcm，圆锥的底面周长等于侧面展开图的扇形弧长，即侧面展开图的扇形弧长是80πcm，母线长为90cm即侧面展开图的扇形的半径长是90cm．根据弧长公式即可计算．
根据弧长的公式l=得到：
80π=，
解得n=160度．
侧面展开图的圆心角为160度．
故答案为160°．
25．
【解析】先求出的长，作点D关于OM的对称点，连接B交OM于点，连接O，则B+ D= B+ =B，此时，BE+DE的最小值= B，进而即可求解．
解：由题意得：OC平分∠MON，
∴∠BOD=，
∴的长=，
作点D关于OM的对称点，连接B交OM于点，连接O，则B+ D= B+ =B，此时，BE+DE的最小值= B，
∵∠AO=∠AOD=∠BOD=20°，
∴∠BO=60 °，
∵O=OD=OB，
∴是等边三角形，
∴B=OB=4，
∴阴影部分周长的最小值=，
故答案是：．

本题主要考查弧长公式以及等边三角形的判定和性质，通过轴对称的性质，构造BE+DE的最小值= B，是解题的关键．
26．
【解析】利用弧长公式进行计算.
解：
故答案为：
本题考查弧长的计算，掌握公式正确计算是本题的解题关键.
27．##
【解析】利用弧长公式计算即可．
解：＝，
故答案为：．
本题考查弧长公式，旋转变换等知识，解题的关键是记住弧长l＝．
28．9
【解析】根据弧长公式L＝求解即可．
∵L＝，
∴R＝＝9．
故答案为9．
本题考查了弧长的计算，解答本题的关键是掌握弧长公式：L＝．
29．##
【解析】利用圆锥的底面周长等于侧面展开图的扇形弧长，根据弧长公式计算．
解：扇形的弧长是：，
圆的半径为，则底面圆的周长是，
圆锥的底面周长等于侧面展开图的扇形弧长则得到：，
即：，
与之间的关系是．
故答案是：．
本题综合考查有关扇形和圆锥的相关计算，解题的关键是要紧紧抓住两者之间的两个对应关系：（1）圆锥的母线长等于侧面展开图的扇形半径；（2）圆锥的底面周长等于侧面展开图的扇形弧长．
30．13.
【解析】由扇形弧长求出底面半径，由勾股定理即可求出母线AB的长．
解：∵圆锥底面周长=侧面展开后扇形的弧长=
∴OB=，
在Rt△AOB中，AB=，
所以，该圆锥的母线长为13.
故答案为：13．
本题考查圆锥弧长公式的应用，解题的关键是牢记有关的公式．
31．
【解析】首先根据勾股定理计算出长，再根据等边三角形的判定和性质计算出，进而可得，然后再根据弧长公式可得答案．
解：，，∠ACB=90°
∴，，
∴
，
是等边三角形，
，
，
弧长，
故答案为：．
本题考查了弧长的计算、旋转的性质，等边三角形的性质与判定，掌握弧长公式及旋转的性质是解题的关键．
32．
【解析】首先求得从B到B´时，圆心O的运动路线与点F运动的路线相同，即是的长,又由正六边形的内角为120°，求得所对 的圆心角为60°，根据弧长公式计算即可.
解：∵正六边形的内角为120°，
∴∠BAF=120°,
∴∠FAF´=60°,
∴
∴正六边形在桌子上滚动(没有滑动)一周，则它的中心O点所经过的路径长为：

故答案为：

本题考查的是正六边形的性质及正六边形中心的运动轨迹长，找到其运动轨迹是解决本题的关键．
33．
【解析】根据等腰直角三角形的性质可求出AC的长，根据S阴影=S△ABC-2S扇形CEF即可得答案．
∵等腰直角三角形中，，
∴AC=AB=，∠B=∠C=45°，
∴S阴影=S△ABC-2S扇形CEF==，
故答案为：
本题考查等腰直角三角形的性质及扇形面积，熟练掌握面积公式是解题关键．
34．2π﹣4
【解析】连接DO，根据题意，可知∠DAO＝45°，∠DOA＝90°，再根据图形可知阴影部分的面积是扇形CAB的面积减去空白部分BAD的面积再加扇形AOD的面积减△AOD的面积，然后代入数据计算即可．
连接DO，
∵线段AC交以AB为直径的半圆弧的中点D，AB＝4，
∴∠DAO＝45°，∠DOA＝90°，DO＝AO＝2，
∴阴影部分的面积是：（）+（）＝2π﹣4，
故答案为：2π﹣4．

本题主要考查了与圆有关的计算问题，熟练掌握扇形面积公式，将不规则图形面积转化成规则图形面积的和与差是解题的关键．
35．①③．
【解析】连接OC、OB、CF、BE．①先证明，，再由，即可证明结论①正确；
②证明△BOG≌△COH，得出OG=OH，证出△OGH是等腰直角三角形，S△OBG=S△OCH，证明S四边形OGBH=S△BOC=S正方形ABCD=定值即可；
③求出AG=BH，利用等线段代换和等腰直角三角形的性质得△BGH的周长=AB+OG=2+OG，利用垂线段最短得到当OG⊥AB时，OG的长最小，此时OG=1，即可得出结论；
④求出∠BOG的度数，由扇形的面积减去三角形的面积即可得出结论．
如图所示，连接OC、OB、CF、BE．
∵∠BOE+∠BOF＝90°，∠COF+∠BOF＝90°，
∴∠BOE＝∠COF，
∴，
∵，
∴；故①正确，
在△BOG与△COH中，，
∴△BOG≌△COH（ASA），
∴OG＝OH，BG＝CH，
∵∠HOG＝90°
∴△OGH是等腰直角三角形，
∴S△OBG＝S△OCH，
∴S四边形OGBH＝S△BOC＝S正方形ABCD＝定值，故②错误；
∵AB＝BC，BG＝CH，
∴AG＝BH，
∴△BGH的周长＝BG+BH+GH＝BG+AG+OG＝AB+OG＝2+OG，
当OG⊥AB时，OG的长最小，此时OG＝1，
∴△GBH周长的最小值为2+，故③正确；
作OM⊥AB于M，则OM＝BM＝AB＝1，OB＝OM＝，
∴GM＝，
∴tan∠GOM＝＝，
∴∠GOM＝30°，
∵∠BOM＝45°，
∴∠BOG＝45°﹣30°＝15°，
∴扇形BOE的面积＝＝，
∵BG＝1﹣，
∴AG＝1+，
过G作GP⊥BO于P，
∴PG＝PB＝﹣，
∴△OBG的面积＝××（﹣）＝﹣，
∴BG，GE，围成的面积＝扇形BOE的面积﹣△BOG的面积＝﹣+，故④错误；
故答案为：①③．

此题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质、四边形的面积、三角函数、扇形面积公式，解题关键在于掌握计算公式．
36．
【解析】图中三角形的面积是由三块相同的扇形叠加而成，其面积=三块扇形的面积相加，再减去两个等边三角形的面积，分别求出即可．
解：过A作AD⊥BC于D，

∵AB=AC=BC=3，∠BAC=∠ABC=∠ACB=60°，
∵AD⊥BC，
∴BD=CD=，AD=BD=，
∴△ABC的面积为BC•AD=，
S扇形BAC=，
∴莱洛三角形的面积S= cm2，
故答案为：．
本题考查了等边三角形的性质和扇形的面积计算，能根据图形得出莱洛三角形的面积=三块扇形的面积相加、再减去两个等边三角形的面积是解此题的关键．
37．
【解析】连接，由可知，分别求出扇形的面积，再根据阴影部分扇形即可求解
连接，

，
即
的半径为1



扇形
阴影部分扇形


故答案为：
本题考查了圆周角定理，扇形面积公式等知识，掌握以上知识求得是解题的关键．
38．
【解析】连接，，根据点为的中点可得，继而可得为等边三角形，求出扇形的面积，最后用扇形的面积减去扇形的面积，再减去（弓形的面积+的面积）即可求得阴影部分的面积．
连接，，
∵点为的中点，
∴，
∴，，
∴为等边三角形，
∴S扇形AOE，
∴S阴影=S扇形AOB-S扇形COD-(S扇形AOE-S△COE)，
，
，
，
故答案为：．

本题考查了扇形的面积计算，圆的性质，等边三角形的性质，三角形面积的计算等知识点，解答本题的关键是掌握扇形的面积公式：．
39．
【解析】利用勾股定理求出AC及AB的长，根据阴影面积等于求出答案．
解：由旋转得，，=∠BAC＝30°，
∵∠ABC＝90°，∠BAC＝30°，BC＝1，
∴AC=2BC=2，AB=，，
∴阴影部分的面积=

=,
故答案为：．
．
此题考查了求不规则图形的面积，正确掌握勾股定理、30度角直角三角形的性质、扇形面积计算公式及分析出阴影面积的构成特点是解题的关键．
40．.
试题解析：连接OE、AE，

∵点C为OA的中点，
∴∠CEO=30°，∠EOC=60°，
∴△AEO为等边三角形，
∴S扇形AOE=
∴S阴影=S扇形AOB-S扇形COD-（S扇形AOE-S△COE）
=
=
=．

41．
试题分析：过点O作OD⊥BC于点D，交于点E，连接OC，则点E是的中点，由折叠的性质可得点O为的中点，∴S弓形BO=S弓形CO，在Rt△BOD中，OD=DE=R=2，OB=R=4，∴∠OBD=30°，
∴∠AOC=60°，∴S阴影=S扇形AOC=．

考点：扇形面积的计算．
42．
【解析】连接OC，过点C作于点M，由勾股定理可得，利用角所对直角边是斜边的一半可得，，根据三角形面积公式及扇形面积公式分别求出、、、S扇形AOC，再计算即可求解．
解：连接OC，过点C作于点M，如图所示：

∵，
∴是等腰直角三角形，
∵，
∴，
∵，于点D，
∴，BD=AB2−AD2=26，
∴，
，
∵，
∴，
∴，
∴CM=12OC=2，
∴，
，
，
=8+43−4−83π，
．
本题主要考查不规则图形的面积及扇形面积公式，勾股定理解三角形，圆周角定理，角所对直角边是斜边的一半，解题的关键是作辅助线，利用分割法求解．
43．2﹣2
【解析】根据题意可以求得和的度数，然后根据图形可知阴影部分的面积就是矩形的面积与矩形中间空白部分的面积之差再加上扇形与的面积之差的和，本题得以解决．
解：连接，
，，，
，
，
，，
，
阴影部分的面积是：，
故答案为：．

本题考查扇形面积的计算、矩形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
44．
【解析】根据题意，由圆周角定理可得，根据垂径定理进而证明，由，根据扇形面积公式计算即可．
解：∵，
∴，



在中，
在与中



故答案为：
本题考查了垂径定理，解直角三角形，全等三角形的性质与判定，求扇形面积，转化是解题的关键．
45．8π
【解析】圆锥的侧面积=底面周长×母线长÷2．
解：底面半径为2，则底面周长=4π，圆锥的侧面积=×4π×4=8π，
故答案为8π．
本题利用了圆的周长公式和扇形面积公式求解，解题的关键是了解圆锥的侧面积的计算方法，难度不大．
46．3
【解析】圆锥的侧面积=底面周长×母线长÷2，把相应数值代入即可求解．
解：设底面半径为R，则底面周长=2πRcm，
侧面展开图的面积=×2πR×5=5πR=15πcm2，
∴R=3cm．
故答案为3．
本题考查了圆的周长公式和扇形面积公式，掌握相应的公式是解答此题的关键．
47．
【解析】算出围成圆锥的扇形的弧长，除以2π即为圆锥的底面半径，利用勾股定理即可求得圆锥的高．
解：∵将半径为3cm的圆形纸片剪掉三分之一，余下部分围成一个圆锥的侧面，
∴围成圆锥的弧长所对圆心角度数是×360°=240°
围成圆锥的弧长为=4πcm，
∴圆锥的底面半径为4π÷2π=2cm，
∴圆锥的高为=cm．
故答案为cm．
本题考查圆锥的计算；得到圆锥的底面半径是解决本题的突破点；用到的知识点为：圆锥的底面周长等于侧面展开图的弧长．
48．80°
【解析】设圆锥的侧面展开扇形图的圆心角为n°，由于圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长，则根据弧长公式得到，然后解方程即可．
解：设圆锥的侧面展开扇形图的圆心角为n°，
根据题意得，
解得n＝80，
即圆锥的侧面展开扇形图的圆心角为80°．
故答案为：80°．
本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
49．（1）图见详解；（2）①； ②(-1，3)
【解析】（1）根据旋转的定义作出点A、B绕点C逆时针旋转90°得到的对应点，再顺次连接可得；
（2）①根据弧长公式列式计算即可；②根据（1）中所作图形可得点的坐标；
（1）如图所示：

（2）①依题意得： ，
∠AC=90°，
∴点A经过的路径的长为 ，
②由图知点B'的坐标为(-1，3)．
故答案为：① ；②(-1，3)．
本题主要考查作图-旋转变换，解题的关键是根据旋转角度、旋转方向、旋转中心作出对应点；
50．（1）见解析；（2）π
【解析】（1）连接BF，OC，由题意易得∠AFB＝90°，即BF⊥AD，OC⊥CE，进而可得BF∥CE，然后问题可求证；
（2）连接OF，CF，由题意易得∠BOC＝60°，，进而可得CF∥AB，则有阴影部分的面积＝S扇形COF，然后根据扇形面积计算公式可求解．
解：（1）如图1，连接BF，OC，

∵AB是⊙O的直径，
∴∠AFB＝90°，即BF⊥AD，
∵CE是⊙O的切线，OC是⊙O的半径，
∴OC⊥CE，
∵点C为劣弧的中点，
∴OC⊥BF，
∴BF∥CE，
∴CE⊥AD；
（2）如图2，连接OF，CF，

∵OA＝OC，∠BAC＝30°，
∴∠BOC＝60°，
∵点C为劣弧的中点，
∴，
∴∠FOC＝∠BOC＝60°，
∵OF＝OC，
∴∠OCF＝∠COB，
∴CF∥AB，
∴S△ACF＝S△COF，
∴阴影部分的面积＝S扇形COF，
∵AB＝4，
∴FO＝OC＝OB＝2，
∴S扇形FOC＝＝π，
即阴影部分的面积为：π．
本题主要考查切线定理及扇形面积，熟练掌握切线定理及扇形面积是解题的关键．
51．（1）证明见解析；（2）
【解析】（1）连接，先证明，进而得到，于是得到，进而证明是的切线；
（2）分别求出的面积和扇形的面积，利用即可得到答案．
（1）证明：连接，
，
，
平分，
，
，
，
，
，
，
，
，
点在圆上，为圆的半径，
是圆的切线；
（2）在中，，，
，
在中，，
，
，，
，
，
，，
，
，

，
阴影部分的面积为．


本题主要考查了切线的判定以及扇形的面积计算，解（1）的关键是证明，解（2）的关键是求出扇形的面积，此题难度一般．
52．(1)见解析
(2)图中阴影部分的面积为．

【解析】（1）连接OD，BD，推出△OBD是等边三角形，得到∠OBD=60°，BD=OB，求得∠ODF=90°，根据切线的判定定理即可得到结论；
（2）根据已知条件OF=4，根据勾股定理得到DF的长，根据三角形和扇形的面积公式即可得到结论．
(1)
证明：连接OD，BD，


∵AB为⊙O的直径，点D是半圆AB的三等分点，
∴∠BOD=∠AOB=60°，
在△OBD中，∵OB=OD，∠BOD=60°，
∴△OBD是等边三角形，
∴∠OBD=60°，BD=OB，
∵OB=BF，BD=OB，
∴BD=BF，
∴∠BDF=∠F，
∵∠OBD=∠F+∠BDF，
∴∠F=∠BOD=30°，
∵∠F=30°，∠BOD=60°，
∴∠ODF=90°，
∴OD⊥DF，
∵点D在⊙O上，
∴直线DF是⊙O的切线；
(2)
解：∵OB=OD=2，BF=OB，
∴OF=4，
在Rt△ODF中，由勾股定理得，DF=，
∵S△ODF=OD•DF=×2×2=2，S扇形BOD=，
∴图中阴影部分的面积=．
本题考查了切线的判定和性质，等边三角形的判定和性质，勾股定理，扇形面积的计算，正确地作出辅助线是解题的关键．
53．(1)，
(2)

【解析】（1）根据弧长公式和扇形面积公式求解即可；
（2）先求出底面圆的半径，然后利用勾股定理求解即可．
（1）
解：由题意得扇形AOB的弧长，；
（2）
解：如图所示，AH为底面圆的半径，OA为母线长，
由题意可得，，
∴．

本题主要考查了求扇形面积，求弧长，求圆锥的高，勾股定理等等，解题的关键在于能够熟练掌握弧长公式和扇形面积公式．