初中数学北师大版九年级下册1 锐角三角函数优质ppt课件

这是一份初中数学北师大版九年级下册1 锐角三角函数优质ppt课件，共17页。PPT课件主要包含了学习目标，情境导入，知识讲解，随堂训练，课堂小结等内容，欢迎下载使用。

1. 理解正切的意义和与现实生活的联系.2.能够用 表示直角三角形中两直角边的比，表示生活中物体的倾斜程度、坡度（坡比）等.（重点）3.能够根据直角三角形的边角关系，用正切进行简单的计算.（难点）
梯子是我们日常生活中常见的物体.
你会比较两个梯子哪个更陡吗？你有哪些办法？
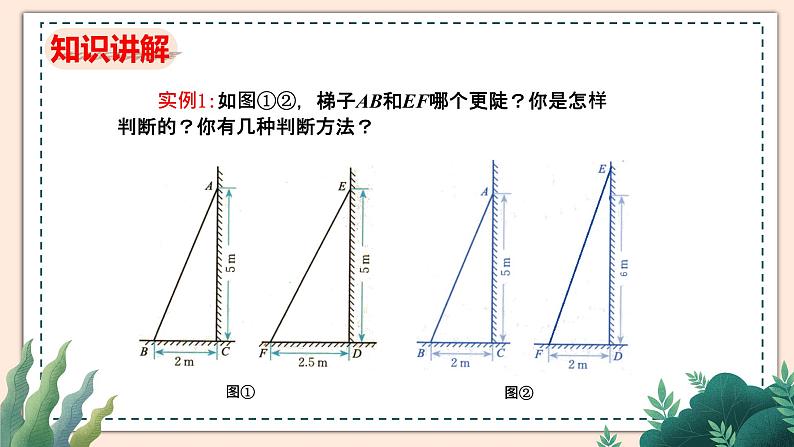
实例1:如图①②，梯子AB和EF哪个更陡？你是怎样判断的？你有几种判断方法？
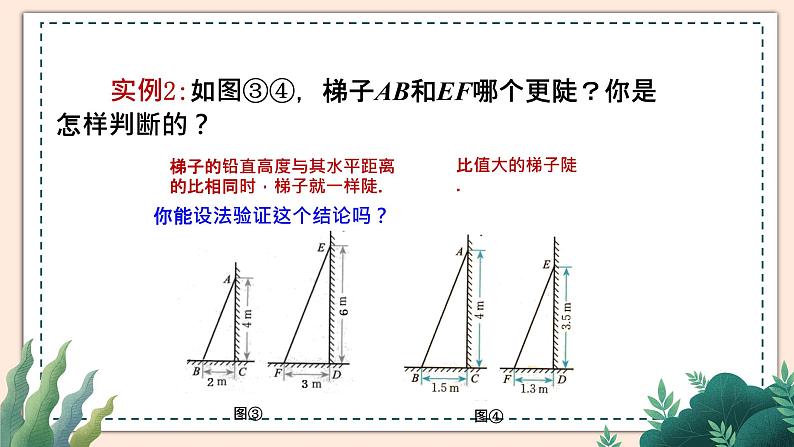
实例2:如图③④，梯子AB和EF哪个更陡？你是怎样判断的？
梯子的铅直高度与其水平距离的比相同时，梯子就一样陡.
你能设法验证这个结论吗？
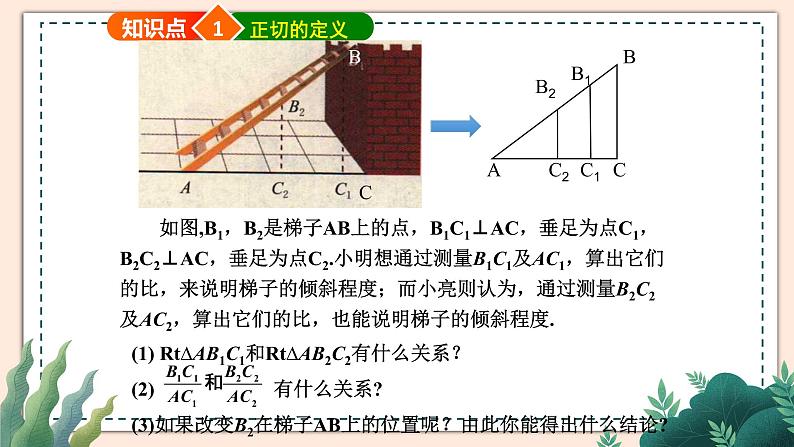
如图,B1，B2是梯子AB上的点，B1C1⊥AC，垂足为点C1，B2C2⊥AC，垂足为点C2.小明想通过测量B1C1及AC1，算出它们的比，来说明梯子的倾斜程度；而小亮则认为，通过测量B2C2及AC2，算出它们的比，也能说明梯子的倾斜程度.
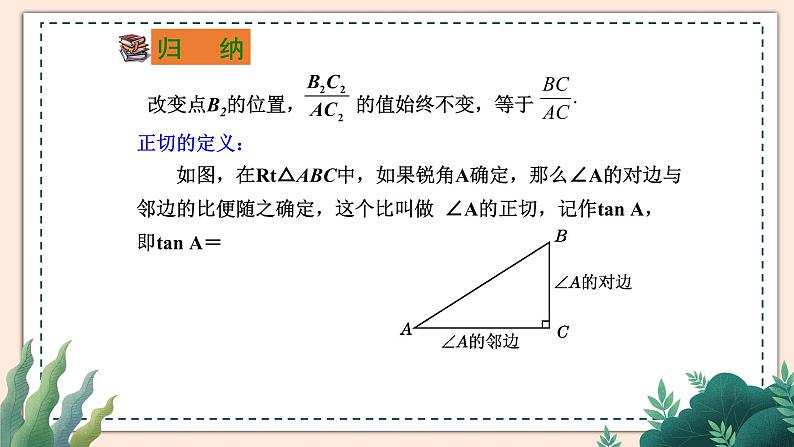
正切的定义： 如图，在Rt△ABC中，如果锐角A确定，那么∠A的对边与邻边的比便随之确定，这个比叫做 ∠A的正切，记作tan A，即tan A＝
定义的几点说明：1）初中阶段，正切是在直角三角形中定义的， ∠A是一个锐角. 2） tanA是一个完整的符号，它表示∠A的正切，记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.3） tanA没有单位，它表示一个比值，即直角三角形中锐角∠A的对边与邻边的比（注意顺序）.4）tanA不表示“tan”乘以“A ”.5） tanA的大小只与∠A的大小有关，而与直角三角形的边长无关
鉴宝专家—--是真是假：
如图,梯子AB的倾斜程度与tanA有怎样的关系?
例1.下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
∵ tanα> tanβ∴甲梯更陡
1.坡面与水平面的夹角(α)叫坡角。2.坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切。3.坡度越大,坡面越陡。
如图,正切也经常用来描述山坡的坡度.例如，有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
1、如图，在Rt△ABC中，∠C＝90°， 则tan A＝___．
2、如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB，垂足为D，则tan∠BCD＝____．
根据题意得∠BCD＝∠CAB，所以tan ∠BCD＝tan ∠CAB＝
3、在Rt△ABC中，∠C＝90°，若斜边AB是直角边BC的3倍，则tan B的值是(　　) A. B．3 C. D．4、 一个直角三角形中，如果各边的长度都扩大为原来的2倍，那么它的两个锐角的正切值(　　) A．都没有变化 　　 B．都扩大为原来的2倍 C．都缩小为原来的一半 D．不能确定是否发生变化
5、如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是(　 ) A．2 B. C. D.
1、理解了正切与坡度的概念.2、tanA的值越大，梯子（坡）越陡3、数形结合的方法；构造直角三角形的意识. 4、“一般 → 特殊 → 一般” 数学思想方法.