






- 1.3《三角函数的计算》课件 课件 8 次下载
- 1.4《解直角三角形》课件 课件 10 次下载
- 1.5《解直角三角形在方向角,仰角、俯角中的应用》课件 课件 9 次下载
- 1.6《利用三角函数测高》课件 课件 9 次下载
- 2.1《二次函数 》课件 课件 10 次下载
数学九年级下册4 解直角三角形完美版ppt课件
展开用解直角三角形解坡角问题(重点、难点)
直角三角形中诸元素之间的关系: (1)三边之间的关系:a2+b2=c2 (勾股定理); (2)锐角之间的关系:∠A+∠B=90°; (3)边角之间的关系:
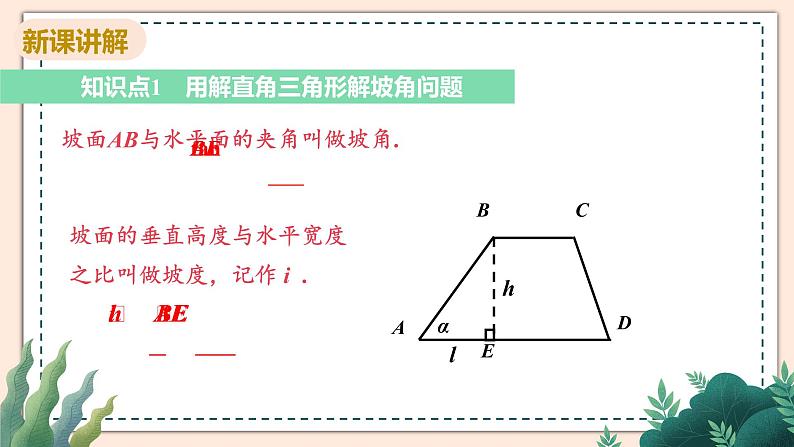
知识点1 用解直角三角形解坡角问题
坡面AB与水平面的夹角叫做坡角.
坡面的垂直高度与水平宽度之比叫做坡度,记作 i .
1.如图 1-5-4,李明在大楼 30 m 高(即 PH=30 m)的窗口 P 处进行观测,测得山坡上 A 处的俯角为 15°,山脚 B处的 俯角为60° . 已知该山坡的坡度 i 为 1 ∶ ,点 P, H, B, C, A 在同一个平面上,点 H, B, C 在同一条直线上,且 PH ⊥ HC.(1)山坡坡角的度数等于________ 度 .(2)求 A, B 两点间的距离(结果精确到 0.1 m,参考数据: ≈ 1.732) .
将分散的条件集中到△ ABP 中求解 .
(1) 30( 2)由题意,得∠ PBH=60°,∠ APB=60°-15°=45° .∵∠ ABC=30°,∴∠ ABP=90°,∴∠ BAP=45°,∴ PB=AB.在 Rt △ PHB 中,
∴ AB=PB=20 ≈ 34.6( m) .即 A, B 两点间的距离约为 34.6 m.
1.如图,水库大坝的横截面是梯形ABCD,其中AD//BC,坝顶AD= 6m坡 长 CD = 8m,坡底 BC=30m, ∠ADC=135°.(1)求∠ABC的度数;(2 )如果坝长100 m,那么建筑这个大坝共需多少土石料?(结果精确到0.01 m3)
(1) 过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.∵AD∥BC,∴四边形AEFD是矩形.∴AD=EF,AE=DF.∵∠ADC=135°,∴∠FDC=45°.在Rt△DCF中,DF=CDcs ∠FDC=8×cs 45°= (m),FC=CDsin ∠FDC=8×sin 45°= (m),∴BE=BC-EF-FC=30-6- =(24- ) m.在Rt△ABE中,tan ∠ABE= = = ≈0.308 4,∴∠ABC≈17°8′23″.
(2) S四边形ABCD= (AD+BC)×DF = ×(6+30)× = (m2), V= ×100≈10 182.34(m3). 所以,建筑这个大坝共需约10 182.34 m3土石料.
2.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin 34°≈0.56,cs 34°≈0.83,tan 34°≈0.67)
知识点2 其他应用
如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).
解:如图,根据题意可知,∠CDB=40°,EC=2m,DB=5m.
∴∠BDE≈51.12°.
答:钢缆DE的长度约为7.96m.
如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长 CD=8m,坡底BC=30m,∠ADC=135°.(1)求坡角∠ABC的大小;(2)如果坝长100m,那么修建这个大坝共需多少土石料? (结果精确到0.01m3 )
(1)解:如图,过点D作DE⊥BC于点E,过点A作AF⊥BC于点F.
∴∠ABC≈17°8′21″.
答:坡角∠ABC约为17°8′21″.
(2)解:如图,
答:修建这个大坝共需土石方约10182.34m3.
1.为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD. 已知迎水坡面AB=12米,背水坡面CD=123米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tan E= ,则CE的长为_______.
2.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin 40°≈0.64,cs 40°≈0.77,tan 40°≈0.84)A.5.1米 B.6.3米 C.7.1米 D.9.2米
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )A.5米 B.6米 C.8米 D.(3+ )米
初中数学23.2解直角三角形及其应用教学ppt课件: 这是一份初中数学<a href="/sx/tb_c44102_t3/?tag_id=26" target="_blank">23.2解直角三角形及其应用教学ppt课件</a>,共12页。PPT课件主要包含了知识要点,新知导入,课程讲授,坡度与坡角的关系,在Rt△ABC中,随堂练习,在Rt△ACD中,∵∠ACD15°等内容,欢迎下载使用。
湘教版九年级上册4.3 解直角三角形优秀课件ppt: 这是一份湘教版九年级上册4.3 解直角三角形优秀课件ppt,共18页。PPT课件主要包含了新课导入,探究新知,i1∶2,AD⊥BC,在Rt△ABD中,ADh35m,由勾股定理得,∴α≈35°,课堂小结等内容,欢迎下载使用。
初中数学湘教版九年级上册4.3 解直角三角形获奖教学课件ppt: 这是一份初中数学湘教版九年级上册4.3 解直角三角形获奖教学课件ppt,文件包含教学课件九上·湘教·44解直角三角形的应用第2课时方向角坡度坡角pptx、数学九上·湘教·44解直角三角形的应用第2课时方向角坡度坡角教案docx等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













