初中4 解直角三角形优质课课件ppt

这是一份初中4 解直角三角形优质课课件ppt，共22页。PPT课件主要包含了学习目标，新课导入，新课讲解，方位角的定义，射线OA，射线OE，射线OF，射线OG，射线OH，认识方位角等内容，欢迎下载使用。

利用解直角三角形解方向角问题（重点、难点）
1.解直角三角形的意义：在直角三角形中，由已知元素 求出所有未知元素的过程，叫做直角三角形.2.直角三角形中诸元素之间的关系： （1）三边之间的关系：a2+b2=c2 (勾股定理）； （2）锐角之间的关系：∠A+∠B=90°； （3）边角之间的关系： 把∠A换成∠B同样适用.
知识点1 用解直角三角形解方向角问题
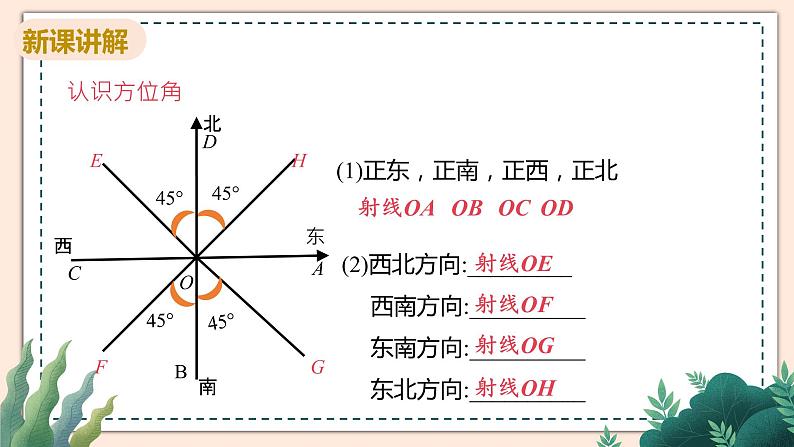
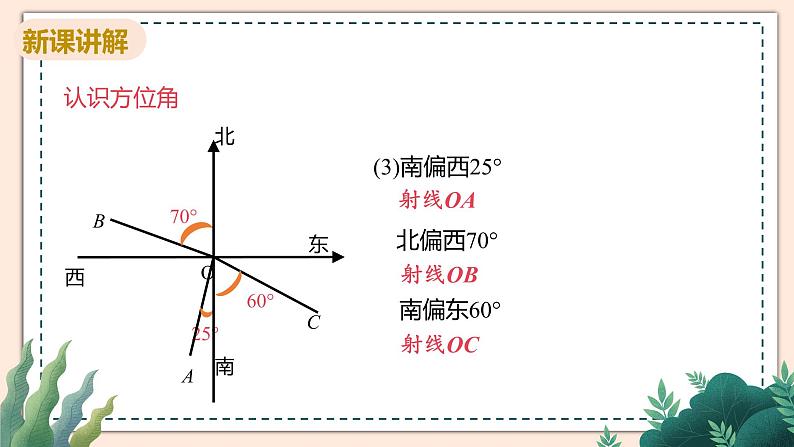
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
(1)正东，正南，正西，正北
(2)西北方向:_________ 西南方向:__________ 东南方向:__________ 东北方向:__________
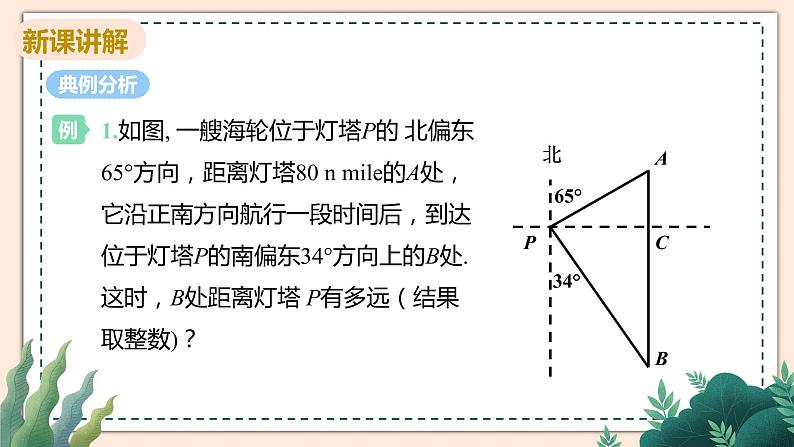
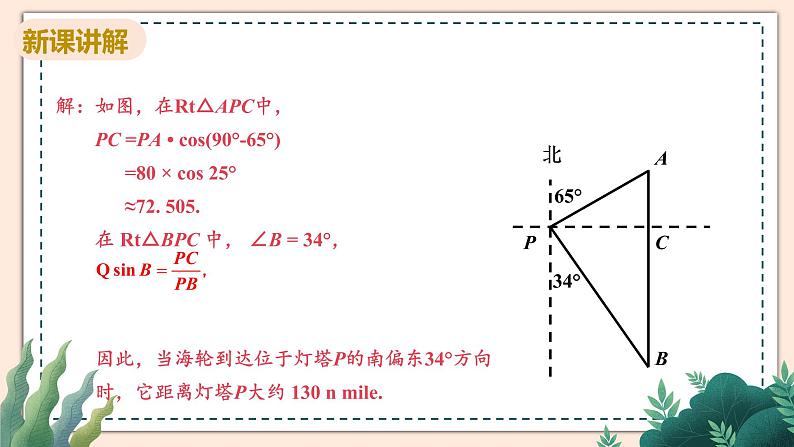
1.如图, 一艘海轮位于灯塔P的 北偏东65°方向，距离灯塔80 n mile的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处.这时，B处距离灯塔 P有多远（结果取整数)？
解：如图，在Rt△APC中， PC =PA • cs(90°-65°) =80 × cs 25° ≈72. 505. 在 Rt△BPC 中， ∠B = 34°， 因此，当海轮到达位于灯塔P的南偏东34°方向 时，它距离灯塔P大约 130 n mile.
如图，已知一条东西走向的河流，在河流对岸有一点A，小明在岸边点B处测得点A在点B的北偏东30°方向上，小明沿河岸向东走80 m后到达点C，测得点A在点C的北偏西60°方向上，则点A到河岸BC的距离为________．
知识点2 仰角、俯角的应用
2. “中国益阳”网上消息，益阳市为了改善市区交通状况，计划在康富路的北端修建通往资江北岸的新大桥.如图，新大桥的两端位于A，B两点，小张为了测量A，B之间的河宽，在垂直于新大桥AB的直线形道路l上测得如下 数据：∠BDA＝76.1°，∠BCA＝68.2°，CD＝82 m．求 AB的长．(结果精确到0.1 m.参考数据：sin 76.1°≈0.97， cs 76.1°≈0.24，tan 76.1°≈4.0； sin 68.2°≈0.93，cs 68.2°≈0.37， tan 68.2°≈2.5)
分析：设AD＝x m，在Rt△ABC中，利用∠BCA的正切值，可以用含x的代数式表示AB.同理在Rt△ABD中，利用∠BDA的正切值表示出AB，从而列出关于x的方程，求出x的值就能求出AB的长了．
设AD＝x m，则AC＝(x＋82) m. 在Rt△ABC中，tan ∠BCA＝∴AB＝AC·tan ∠BCA＝(x＋82)tan 68.2° m. 在Rt△ABD中，tan ∠BDA＝∴AB＝AD·tan ∠BDA＝xtan 76.1° m.∴(x＋82)tan 68.2°＝xtan 76.1°.∴x≈136.67.∴AB≈4×136.67≈546.7(m)． 即AB的长约为546.7 m.
如图，AB是斜靠在墙上的长梯，D是梯上一点，梯脚B与墙脚的距离为1.6 m(即BC的长)，点D与墙的距离为1.4 m(即DE的长)，BD长为0.55 m，则梯子的长为(　　)A．4.50 m B．4.40 m C．4.00 m D．3.85 m
3. 如图 1-5-5，某居民楼Ⅰ高 20 m，窗户朝南，该楼内一楼住户的窗台离地面的距离 CM 为 2 m，窗户 CD 高 1.8 m.现计划在楼Ⅰ的正南方距楼Ⅰ 30 m 处新建一居民楼Ⅱ . 当正午时刻太阳光线与地面成 30°角时，要使楼Ⅱ的影子不影响楼Ⅰ所有住户的采光，新建楼Ⅱ最高只能建多少米？
设正午时刻太阳光线正好照在楼Ⅰ 一楼的窗台处，此时新建居民楼Ⅱ高 EG=x m，如图 1-5-5，过 C 作 CF ⊥ EG 于 F，则 FG=CM=2 m.在 Rt △ ECF 中， EF=（ x-2） m， FC=30 m，∠ECF=30°，即新建楼Ⅱ 最高只能建
如图，AB是伸缩式遮阳棚，CD是窗户，要想在夏 至的正午时刻阳光刚好不能射入窗户，则AB的长 是________米．(假设夏 至的正午时刻阳光与地 平面的夹角为60°)
如图，已知电线杆AB直立于地面上，它的影子恰好 照在土坡的坡面CD和地面BC上，如果CD与地面成 45°，∠A＝60°，CD＝4 m，BC＝(4 －2 ) m，则电线杆AB的长为________．
解决与方位角有关的实际问题时，必须先在每个位置中心建立方向标，然后根据方位角标出图中已知角的度数，最后在某个直角三角形内利用锐角三角函数解决问题．
1 如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的A处．如果海轮沿正南方向航行到灯塔的正东位置，则海轮航行的距离AB是(　　) A．2海里 B．2sin 55°海里 C．2cs 55°海里 D．2tan 55°海里
2.如图，一艘轮船在A处测得灯塔P位于其北偏东60°方向上，轮船沿正东方向航行30海里到达B处后，此时测得灯塔P位于其北偏东30°方向上，此时轮船与灯塔P的距离是(　　)A．15 海里 B．30海里C．45海里 D．30海里
如图，在距离铁轨200米的B处，观察由南宁开往百色的“和谐号”动车，当动车车头在A处时，恰好位于B处的北偏东60°方向上；10秒钟后，动车车头到达C处，恰好位于B处的西北方向上，则这时段动车的平均速度是(　　)米/秒．A．20( ＋1) B．20( －1)C．200 D．300