初中数学北师大版九年级下册5 确定圆的条件评优课ppt课件

这是一份初中数学北师大版九年级下册5 确定圆的条件评优课ppt课件，共22页。PPT课件主要包含了两个条件，探索一，探索二，探索三，画一画，三角形与圆的位置关系，找一找，植物园，动物园，人工湖等内容，欢迎下载使用。

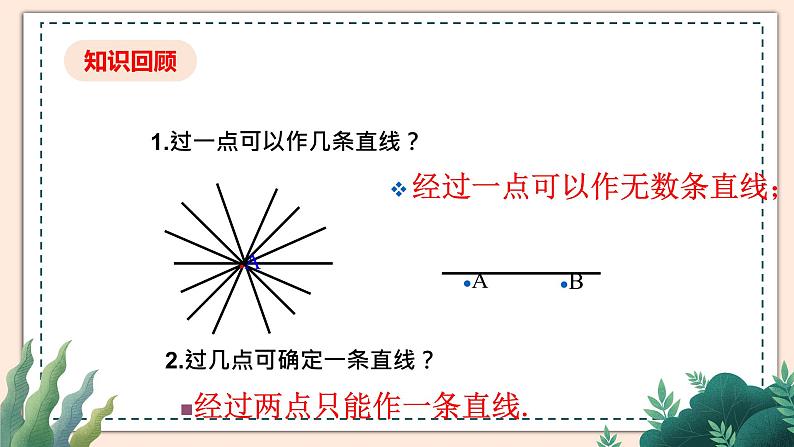
1.过一点可以作几条直线？
经过一点可以作无数条直线；
2.过几点可确定一条直线？
经过两点只能作一条直线.
过几点可以确定一个圆呢？
思考：构成圆的基本要素有那些?
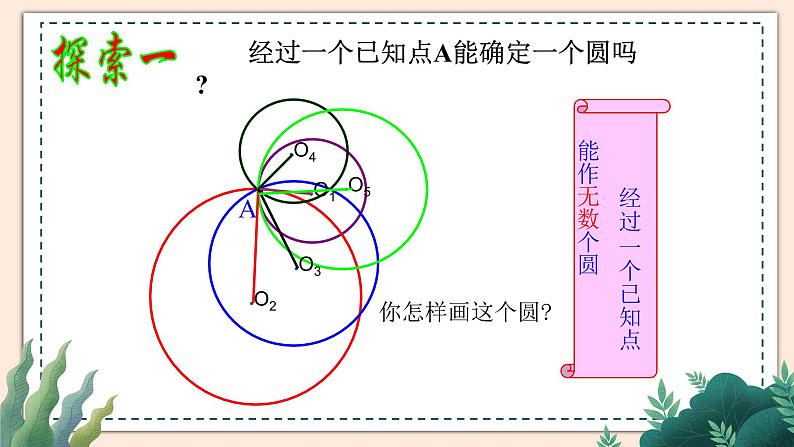
经过一个已知点A能确定一个圆吗?
经过一个已知点能作无数个圆
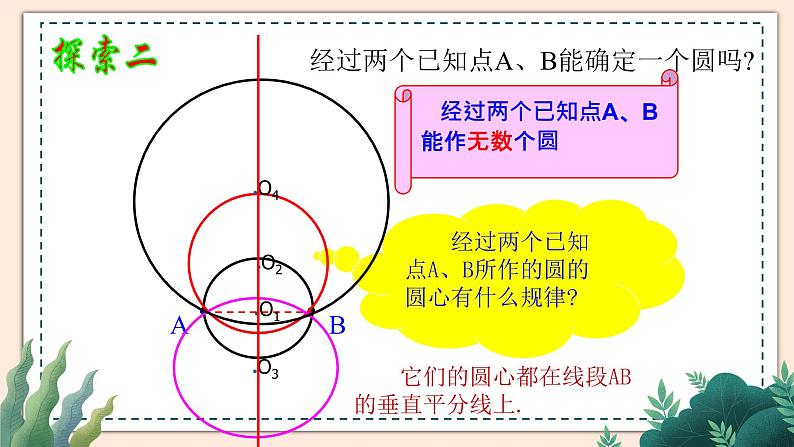
经过两个已知点A、B能确定一个圆吗?
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心有什么规律?
它们的圆心都在线段AB的垂直平分线上.
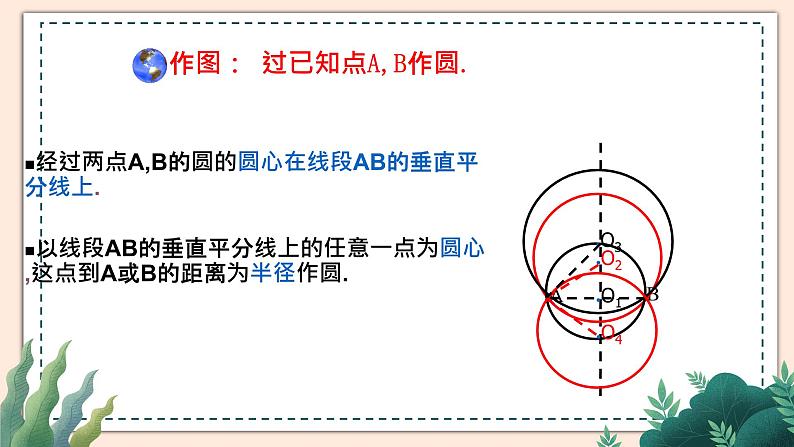
作图： 过已知点A,B作圆.
经过两点A,B的圆的圆心在线段AB的垂直平分线上.以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
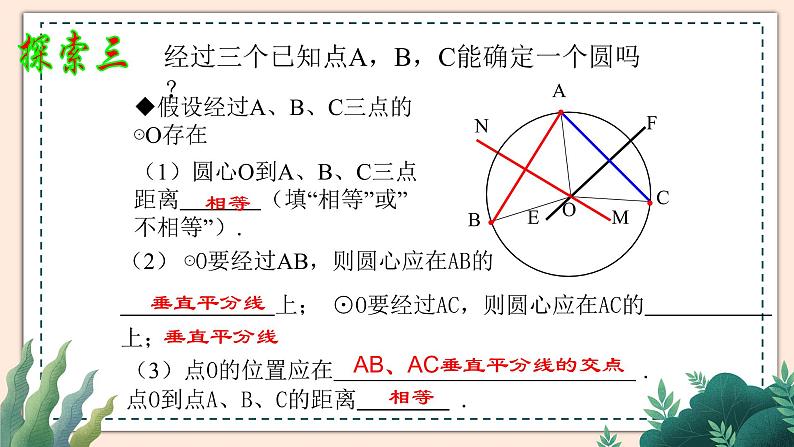
经过三个已知点A，B，C能确定一个圆吗？
假设经过A、B、C三点的⊙O存在
（1）圆心O到A、B、C三点距离 （填“相等”或”不相等”）.
（2） ⊙O要经过AB，则圆心应在AB的 上； ⊙O要经过AC，则圆心应在AC的 上；
（3）点O的位置应在 .点O到点A、B、C的距离 .
AB、AC垂直平分线的交点
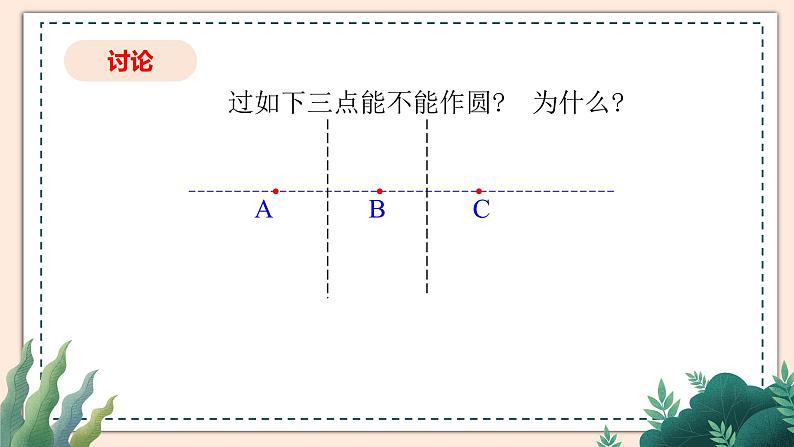
过如下三点能不能作圆? 为什么?
已知：不在同一直线上的三点A、B、C 求作： ⊙O使它经过点A、B、C.
作法：（1）连接AB，作线段AB的垂直平分线MN；（2）连接AC，作线段AC的垂直平分线EF，交MN于点O；（3）以O为圆心，OB为半径作圆.所以⊙O就是所求作的圆.
不在同一直线上的三点确定一个圆
经过三角形各个顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形.
如图：⊙O是△ABC的外接圆， △ABC是⊙O的内接三角形，点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点，它到三角形的三个顶点的距离相等.
分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况.
锐角三角形的外心位于三角形内直角三角形的外心位于直角三角形斜边中点注：（斜边长等于直径，圆的半径等于斜边的一半）钝角三角形的外心位于三角形外.
如何将一个如图所示的破损的圆盘复原？
方法:(1)在圆弧上任取三点A、B、C.(2)作线段AB、BC的垂直平分线,其交点O即为圆心.(3)以点O为圆心，OC长为半径作圆.⊙O即为所求.
如图，请找出图中圆的圆心，并写出你找圆心的方法?
某市要建一个圆形公园，要求公园刚好把动物园A，植物园B和人工湖C包括在内，又要使这个圆形的面积最小，请你给出这个公园的施工图.（A、B、C不在同一直线上）
图中工具的CD边所在直线恰好垂直平分AB边，怎样用这个工具找出一个圆的圆心.
1.（河北·中考）如图，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（ ）
A．点P B．点Q C．点R D．点M
2.（乌鲁木齐·中考）如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，4），（5，4），（1，-2），则△ABC的外接圆的圆心的坐标是（ ）A.（2，3） B.（3，2）C.（1，3） D.（3，1）
3.（江西·中考）如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为（4，2），点A的坐标为（2，0），则点B的坐标 ．
4.（湖州·中考）请你在如图所示的12×12的网格图形中任意画一个圆，则所画的圆最多能经过169个格点中的 个格点．
【规律方法】外心是三边中垂线的交点，它到三个顶点的距离相等，在数学和实际运用中，要分析清楚题意，转化为数学问题要明确已知什么，求作什么.