专题 18.35 特殊平行四边形动点问题专题训练（巩固篇）（专项练习）-八年级数学下册基础知识专项讲练（人教版）

这是一份专题 18.35 特殊平行四边形动点问题专题训练（巩固篇）（专项练习）-八年级数学下册基础知识专项讲练（人教版），共39页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

专题 18.35 特殊平行四边形动点问题专题训练（巩固篇）
（专项练习）
一、单选题
1．如图，在平行四边形ABCD中，∠DAB＝120°，AB＝4，AD＝2，点O为对称中心，点M从点A出发沿AB向点B运动，到点B停止运动，连接MO并延长交CD于点N，则四边形AMCN形状的变化依次为（ ）

A．平行四边形→正方形→平行四边形→矩形→平行四边形
B．平行四边形→菱形→平行四边形→矩形→平行四边形
C．平行四边形→矩形→菱形→正方形→平行四边形
D．平行四边形→菱形→正方形→矩形→平行四边形
2．在平面直角坐标系中，长方形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA＝3，OB＝4，D为边OB的中点，若E为x轴上的一个动点，当△CDE的周长最小时，求点E的坐标（ ）

A．（一3，0） B．（3，0） C．（0，0） D．（1，0）
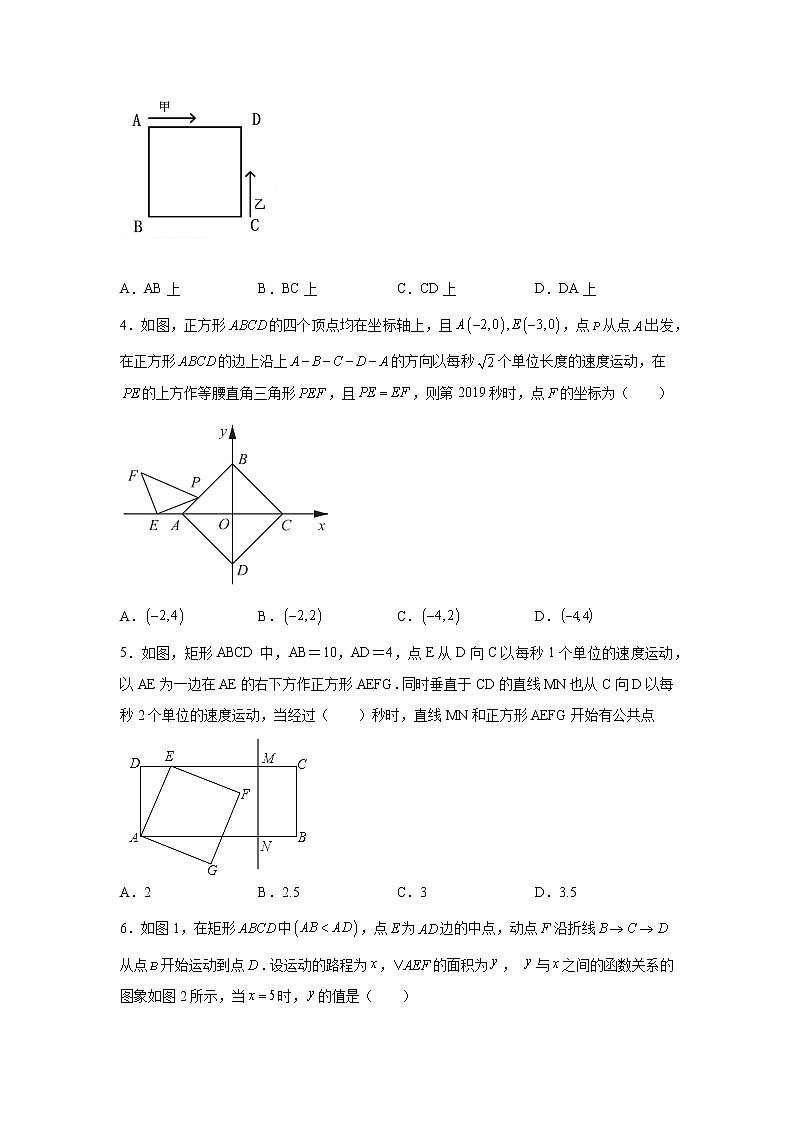
3．如图，甲､乙两动点分别从正方形ABCD的顶点A､C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的速度的4倍，则它们第2017次相遇在边( )


A．AB上 B．BC上 C．CD上 D．DA上
4．如图，正方形的四个顶点均在坐标轴上，且，点从点出发，在正方形的边上沿上的方向以每秒个单位长度的速度运动，在的上方作等腰直角三角形，且，则第2019秒时，点的坐标为（ ）

A． B． C． D．
5．如图，矩形ABCD中，AB＝10，AD＝4，点E从D向C以每秒1个单位的速度运动，以AE为一边在AE的右下方作正方形AEFG．同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动，当经过（ ）秒时，直线MN和正方形AEFG开始有公共点

A．2 B．2.5 C．3 D．3.5
6．如图1，在矩形中，点为边的中点，动点沿折线从点开始运动到点．设运动的路程为，的面积为， 与之间的函数关系的图象如图2所示，当时，的值是（ ）

A． B． C． D．
7．在平面直角坐标系中，长为2的线段（点D在点C右侧）在x轴上移动，，连接、，则的最小值为（ ）

A． B． C． D．
8．如图，在矩形ABCD中，AB＝4cm，AD＝12cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在这段时间内，线段PQ平行于AB的次数是（　　）

A．2 B．3 C．4 D．5
9．如图，平面直角坐标系xOy中，点A在第一象限，B（2，0），∠AOB＝60°，∠ABO＝90°．在x轴上取一点P（m，0），过点P作直线l垂直于直线OA，将OB关于直线l的对称图形记为O′B′，当O′B′和过A点且平行于x轴的直线有交点时，m的取值范围为（　　）

A．m≥4 B．m≤6 C．4＜m＜6 D．4≤m≤6
10．如图，在菱形中，，，点是线段上一动点，点是线段上一动点，则的最小值（ ）

A． B． C． D．
11．如图，在正方形中，，延长到点，使，连接，动点从点出发以每秒1个单位长度的速度沿向终点运动．设点的运动时间为秒.当和全等时，的值为（ ）

A．3 B．5 C．7 D．3或7
12．如图所示，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动，设点D，E运动的时间是ts（0＜t≤15），过点D作DF⊥BC于点F，连接DE，EF，若四边形AEFD为菱形，则t的值为（ ）

A．20 B．15 C．10 D．5
13．如图①，点从菱形的顶点出发，沿以的速度匀速运动到点．图②是点运动时，的面积（）随着时间（）变化的关系图象，则菱形的边长为（ ）

A． B． C． D．


二、填空题
14．如图．在正方形的边上有一点，连接．点从正方形的顶点出发，沿以的速度匀速运动到点．图是点运动时，的面积随时间变化的函数图象．

（1）正方形的边长为______．
（2）当时，的值为______．
15．如图，在四边形ABCD中，AD∥BC，且，，P，Q分别从A，C同时出发，以的速度由向运动，Q以2cm/s的速度由C出发在射线CB上运动，设运动时间为x秒，当___时，以A、B、Q、P为顶点的四边形是平行四边形．

16．如图，在矩形中，是上一点，是上一动点，连接，取的中点，连接，当线段取得最小值时，线段的长度是_________．

17．我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点处，点E为x轴上一动点，当取最小值时，点E的坐标为____．

18．如图，在边长为8厘米的正方形中，动点在线段上以2厘米/秒的速度由点向点运动，同时动点在线段上以1厘米/秒的速度由点向点运动，当点到达点时整个运动过程立即停止．设运动时间为1秒，当时，的值为______．

19．如图，在中，，，点D是AB上一动点，以AC为对角线的所有平行四边形ADCE中，DE的最小值是________．

20．如图，中，AB=7，BC=5，CH⊥AB于点H，CH=4， 点P从点D出发， 以每秒1个单位长度的速度沿DC-CH向点H运动，到点H停止，设点P的运动时间为t

（1）AH=__________．
（2）若△PBC是等腰三角形， 则t的值为__________．
21．如图，△ 中，∠，∠，，点是上的一个动点，点关于，的对称点分别是和F，四边形是平行四边形，则四边形的面积的最小值是________．

22．如图，正方形的边长是16，点在边上，，点是边上不与点、重合的一个动点，把沿折叠，点落在处，若恰为等腰三角形，则的长为______．

23．如图，在平行四边形中，点在上，，点是的中点，若点以1厘米/秒的速度从点出发，沿向点运动；点同时以2厘米/秒的速度从点出发，沿向点运动，点运动到停止运动，点也同时停止运动，当点运动时间是_____秒时，以点为顶点的四边形是平行四边形．

24．如图，已知矩形ABCD中，AB=6，AD=10，动点P从点D出发，在边DA上以每秒1个单位的速度向点A运动，连接CP，作点D关于直线PC的对称点E，设点P的运动时间为t(x)，当P，E，B三点在同一直线上时对应t的值为　 　．

25．如图，▱ABCD中，AB＝2，BC＝4，∠B＝60°，点P是四边形上的一个动点，则当△PBC为直角三角形时，BP的长为_____．


三、解答题
26．如图，在平行四边形中，，．．点在上由点向点出发，速度为每秒；点在边上，同时由点向点运动，速度为每秒．当点运动到点时，点，同时停止运动．连接，设运动时间为秒．
（1）当为何值时，四边形为平行四边形？
（2）设四边形的面积为，求与之间的函数关系式．
（3）当为何值时，四边形的面积是四边形的面积的四分之三？求出此时的度数．
（4）连接，是否存在某一时刻，使为等腰三角形？若存在，请求出此刻的值；若不存在，请说明理由．

27．如图，在长方形ABCD中，AB=6cm，BC=12cm，点P从A点出发沿A-B-C-D移动，且点P的速度是2cm/s，设运动的时间为t秒，若点P与点A、点D连线所围成的三角形PAD的面积表示为S1．
（1）当t=2秒时，求S1 =______cm2；
（2）当S1=12cm2时，则t=______秒；
（3）如图2，若在点P运动的同时，点Q也从C点同时出发，沿C-B运动，速度为1cm/s，若点Q与点C、点D连线所围成的三角形QCD的面积表示为S2，当|S1－S2|=18时，求t的值．

28．如图，在中，，，．点从点出发沿方向以每秒2个单位长的速度向点匀速运动，同时点从点出发沿方向以每秒1个单位长的速度向点匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点、运动的时间是秒（）．过点作交于点，连接、．
（1）求证；
（2）四边形能够成为菱形吗？如果能，求出相应的值；如果不能，说明理由．
（3）当为何值时，为直角三角形？请说明理由．


























参考答案
1．B
【分析】
根据OM与OA的位置关系，数量关系，两个方面去判断
【详解】
如图，连接AC，
∵四边形ABCD是平行四边形，
∴OA=OC，AM∥NC，
∴∠MAO=∠NCO，∠AMO=∠CNO，
∴△MAO≌△NCO，
∴MO=NO，
∴四边形ANCM是平行四边形，
当∠AOM=90°时，
四边形ANCM是菱形，
当∠AOM＞90°，且OA≠OM时，
四边形ANCM是平行四边形，
当∠AOM＞90°，且OA=OM时，
四边形ANCM是矩形，
当∠AOM＞90°，且OA≠OM时，
四边形ANCM是平行四边形，
∴选B．

【点拨】本题考查了平行四边形的性质和判定，菱形的判定，矩形的判定，熟练掌握对角线与四边形的形状之间的关系是解题的关键．
2．D
【分析】
由于C、D是定点，则CD是定值，如果△CDE的周长最小，即DE＋CE有最小值．为此，作点D关于x轴的对称点D′，当点E在线段CD′上时，△CDE的周长最小．
【详解】
如图，作点D关于x轴的对称点D′，连接CD′与x轴交于点E，连接DE．
若在边OA上任取点E′与点E不重合，连接CE′、DE′、D′E′
由DE′＋CE′＝D′E′＋CE′＞CD′＝D′E＋CE＝DE＋CE，
∴△CDE的周长最小．
∵OB＝4，D为边OB的中点，
∴OD＝2，
∴D（0，2），
∵在长方形OACB中，OA＝3，OB＝4，D为OB的中点，
∴BC＝3，D′O＝DO＝2，D′B＝6，
∵OE∥BC，
∴Rt△D′OE∽Rt△D′BC，
∴，
即：，即：OE＝1，
∴点E的坐标为（1，0）
故选：D．

【点拨】此题主要考查轴对称−−最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是：两点之间线段最短．
3．C
【分析】
第一次相遇行走路程为2a,第二次路程为4a…第n次还是4a,而他们的速度和为5v，求每次甲走的路程，甲第一次走的路程为S1=，第二次走的路程为S2=，第n次走的路程为Sn =，然后求出甲一共走的路程被一周4a除看有多少圈，最后考虑余下的圈数乘以一周4a即可．
【详解】
设正方形的边长为a，甲的速度为v,则乙的速度为4v，
第一次相遇时间为t1，第二次相遇时间为t2，第n次相遇时间为tn，
甲第一次走的路程为S1，第二次走的路程为S2，第n次走的路程为Sn，
4vt1+vt1=2a，
t1=，S1=v•t1=，
4vt2+vt2=4a，
t2=，S2= v•t2=，
4vt3+vt3=4a，
t3=，S3= v•t3=，
…
tn=，Sn= v•tn=，
S=S1+S2+…+Sn=++…+=，
当n=2017时，
S=，
S÷4a=403.3圈，
0.3×4a=1.2a，
第2017次相遇在CD上距离D为0.2a．
故选择：C．
【点拨】本题考查相遇地点问题，关键是以甲还是乙为考查对象，然后计算他们走的总路程，被一周4a除看余数，掌握路程时间与速度关系，确定好每次走的路程，第一次2a，以后都是4a才能得以解决问题．
4．D
【分析】
根据A点坐标可得正方形ABCD的边长，且P点运行2019秒，可得P点最后运动到BC中点，即点P坐标为(1,1),且PEF为等腰直角三角形，可得F点坐标．
【详解】
解：在正方形ABCD中，A点坐标(-2,0),
∴正方形ABCD边长AB=，
又∵点P沿着A-B-C-D-A的方向，以每秒个单位长度运动2019秒，
∴点P所经过路程为，此时P点运动到BC中点，
∴点P坐标为(1,1),点E坐标为(-3,0),且PEF为等腰直角三角形，
∴点F坐标为(-4,4)，
故选：D．
【点拨】本题考察了特殊平行四边形中的动点问题及坐标系中点坐标的描述，解题的关键在于判断出点P在运动了2019秒后停止的位置．
5．A
【分析】
首先过点F作FQ⊥CD于点Q，证明△ADE≌△EQF，进而得出AD=EQ，得出当直线MN和正方形AEFG开始有公共点时：DQ+CM≥10进而求出即可．
【详解】
解：过点F作FQ⊥CD于点Q，

∵在正方形AEFG中，∠AEF=90°，AE=EF，
∴∠1+∠2=90°，
∵∠DAE+∠1=90°，
∴∠DAE=∠2，
在△ADE和△EQF中，

∴△ADE≌△EQF（AAS），
∴AD=EQ=4，
当直线MN和正方形AEFG开始有公共点时,此时时间为t,则有DQ+CM≥10，
∴t+4+2t≥10，
解得：t≥2，
故当经过2秒时．直线MN和正方形AEFG开始有公共点．
故选：A．
【点拨】本题考查了全等三角形的判定和性质，正方形、矩形的性质，熟练掌握正方形的四边相等且每个角为90°，矩形的四个角为90°；通过三角形全等将EQ转化为AD，可以表示出DQ+CM的长；本题有动点运动问题，要会表示动点的路程：时间×速度．
6．A
【分析】
根据题意，当点F在线段BC上时，y=3不变，当点F由C到D时，y逐渐变小，然后列出方程组，求出BC和CD的长度，即可求出答案．
【详解】
解：根据题意，可知
当点F在线段BC上时，y=3不变，
∵点E是AD的中点，则
，
∴，
当点F由C到D时，y逐渐变小，则有
，
∵
∴，，
当时，点F在CD上，则，
∴，
∴；
故选：A．
【点拨】本题考查动点问题的函数图象，矩形的性质，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考常考题型．
7．B
【分析】
作A（0，2）关于x轴的对称点A’（0，-2），再过A’作A’E∥x轴且A’E=CD=2，连接BE交x轴与D点，过A’作A’C∥DE交x轴于点C，得到四边形CDEA’为平行四边形，故可知AC+BD最短等于BE的长，再利用勾股定理即可求解．
【详解】
作A（0，2）关于x轴的对称点A’（0，-2）
过A’作A’E∥x轴且A’E=CD=2，故E（2，-2）
连接BE交x轴与D点
过A’作A’C∥DE交x轴于点C，
∴四边形CDEA’为平行四边形，
此时AC+BD最短等于BE的长，
即AC+BD=A’C+BD=DE+BD=BE==
故选B．

【点拨】此题主要考查最短路径的求解，解题的关键是熟知直角坐标系、平行四边形的性质．
8．C
【分析】
当QP∥AB时，由AP∥BQ可得到ABQP为平行四边形，然后依据矩形的性质可得到AP＝BQ，然后求得AP＝BQ的次数即可．
【详解】
解：当QP∥AB时，
∵在在矩形ABCD，AD∥BC，
∴四边形ABQP为平行四边形，
∴AP＝BQ，
∵点P运动的时间＝12÷1＝12秒，
∴点Q运动的路程＝4×12＝48cm．
∴点Q可在BC间往返4次．
∴在这段时间内PQ与AB有4次平行．
故选：C．
【点拨】本题考查了平行四边形的判定．注意能求出符合条件的所有情况是解此题的关键，注意掌握分类讨论思想的应用．
9．D
【分析】
根据题意可以作出合适的辅助线，然后根据题意，利用分类讨论的方法可以计算出m的两个极值，从而可以得到m的取值范围．
【详解】
解：如图所示，

当直线l垂直平分OA时，O′B′和过A点且平行于x轴的直线有交点，
∵点A在第一象限，B（2，0），∠AOB＝60°，∠ABO＝90°，
∴∠BAO＝30°，OB＝2，
∴OA＝4，
∵直线l垂直平分OA，点P（m，0）是直线l与x轴的交点，
∴OP＝4，
∴当m＝4；
作BB″∥OA，交过点A且平行于x轴的直线与B″，
当直线l垂直平分BB″和过A点且平行于x轴的直线有交点，
∵四边形OBB″O′是平行四边形，
∴此时点P与x轴交点坐标为（6，0），
由图可知，当OB关于直线l的对称图形为O′B′到O″B″的过程中，点P符合题目中的要求，
∴m的取值范围是4≤m≤6，
故选：D．
【点拨】本题考查坐标与图形的变化−对称，解答本题的关键是明确题意，作出合适的辅助线，利用数形结合的思想解答．
10．D
【分析】
先作点E关于AC的对称点点G，再连接BG，过点B作BH⊥CD于H，运用勾股定理求得BH和GH的长，最后在Rt△BHG中，运用勾股定理求得BG的长，即为PE+PF的最小值．
【详解】
解：作点E关于AC的对称点点G，连接PG、PE，则PE=PG，CE=CG=2，
连接BG，过点B作BH⊥CD于H，则∠BCH=∠CBH=45°，

∵四边形ABCD是菱形，
∴
∴Rt△BHC中，BH=CH= ，
∴HG=HC-GC=3-2=1，
∴Rt△BHG中，BG= ，
∵当点F与点B重合时，PE+PF=PG+PB=BG（最短），
∴PE+PF的最小值是．
故选：D．
【点拨】本题以最短距离问题为背景，主要考查了菱形的性质与轴对称的性质，凡是涉及最短距离的问题，一般要考虑线段的性质定理，一般情况要作点关于某直线的对称点．注意：如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．
11．D
【分析】
分两种情况，①当点P在BC边上时，②当点P在AD边上时，找出对应的边列式计算即可.
【详解】
当点在边上时，在与中，
，
∴．
由题意得，
∴．
当点在上时，在与中，
，
∴，
由题意得，解得．
当点在上时，不满足条件．
∴当的值为3或7时，和全等．
故选D．
【点拨】本题考查的是正方形的性质和全等三角形的性质，能够分情况讨论是解题的关键.
12．C
【解析】
【分析】
利用t分别表示出CD和AE的长，根据四边形AEFD为菱形可得AD=AE，列方程求出t值即可.
【详解】
∵点D和点E的速度分别为4cm/s和2cm/s，
∴CD=4t，AE=2t，
∵四边形AEFD为菱形，
∴AD=AE，即60-4t=2t，
解得：t=10，
故选C.
【点拨】本题考查菱形的性质，用t分别表示出CD和AE的长并熟练掌握菱形的四条边都相等的性质是解题关键.
13．C
【分析】
根据图②可以发现点E运动5秒后△ABE的面积停止了变化，且为最大面积，由此结合图①，当点E在CD上运动时，△ABE面积最大，从而得出AC=5，CD=，然后根据△ABE最大面积为2得出△ABC面积为2，所以菱形ABCD面积为4，从而再次得出△ABC的高为4，然后进一步利用勾股定理求出菱形边长即可.
【详解】

如图，过C点作AB垂线，交AB于E，
由题意得：△ABC面积为2，AC=5，DC=，
∵四边形ABCD是菱形，
∴AB=DC=BC=,
∴△ABC面积==2，
∴CE=4，
∴在Rt△AEC中，AE==3，
∴BE=，
∴在Rt△BEC中，，
即，
解得：.
∴菱形边长为.
故选：C.
【点拨】本题主要考查了菱形与三角形动点问题的综合运用，熟练掌握相关性质是解题关键.
14．
【分析】
（1）抓住关键点，函数图象最高点的纵坐标为8，得△APE的最大面积为8，此时P、D重合，y＝AD•AB＝8，即可求解；
（2）先抓住关键点，知道点P到终点时，△APE的面积是6，此时P、C重合，y＝EC•AB＝6，得EC＝3，根据图象分析当x＝7时，点P在CD上，且PD＝3，再求△APE的面积．
【详解】
解：（1）设正方形的边长为a，
由图象可知，当P、D重合时，△APE的面积为8，
∴y＝AD•AB＝8，
∴a2＝8，
解得：a＝4（−4舍去），
∴正方形的边长为4，
故答案为：4；
（2）当点在点时，，
解得：，即，，
当x＝7时，点P在CD边上，如图，

y＝S正方形ABCD−S△ABE−S△PEC−S△APD
＝4×4−×4×1−×3×1−×4×3＝，
故答案为：．
【点拨】本题考查的是动点图象问题，解决此类问题关键是：弄清楚不同时间段，函数图象和图形的对应关系，进而求解．
15．2或6
【分析】
以A、B、Q、P为顶点的四边形是平行四边形．分情况分析，当点Q位于B点右侧时，有，当点Q位于点B左侧时，有，据此回答即可．
【详解】
解：运动时间为x秒，
，
当Q位于B点右边时，
四边形ABQP为平行四边形，
，
，
；
当Q位于B点左侧时，
四边形AQBP为平行四边形时，
,，
，
解得：；
故答案为：2或6．
【点拨】本题主要考查平行四边形的性质，根据平行四边形的性质列出关于x的方程是解题的关键，注意分类讨论．
16．5
【分析】
过点P作PM∥FE交AD于M，则FE为△APM的中位线，，当时，PM最短，EF最短，在Rt△PMD中可求得PD的长度．
【详解】
解：过点P作PM∥FE交AD于M，如图，

∵F为AP的中点， ，
∴FE为△APM的中位线，
∴ ，
当EF取最小值时，即PM最短，
当时，PM最短，
此时 ，
∵，
在 中，，
∴当线段EF取得最小值时，线段PD的长度是5，
故答案为：5．
【点拨】本题考查了矩形的性质，垂线段的性质和三角形中位线定理，构造三角形中位线，利用垂线段最短是解决本题的关键PM⊥AD．
17．
【分析】
首先根据题意作图找到点的位置，然后由正方形性质得到，再利用勾股定理得到 ，进而得到点的坐标，最后利用待定系数法可得到直线 的解析式，求出点的坐标即可．
【详解】
解：作关于轴对称的点，连接 与轴的交点即为所求点．


∵轴垂直平分，
∴
∴
即当动点在点的位置时，的值最小
∵，
∴，
∴，，
∴直线的函数解析式为：，
∴点的坐标为．
故答案为．
【点拨】本题考查了最短距离问题、正方形的性质、待定系数法求一次函数解析式等知识点，准确的找到点所在的位置是解决本题的关键．
18．
【分析】
由“ASA”可证△ABQ≌△DAP，可得AP＝BQ，列出方程可求t的值．
【详解】
∵四边形ABCD是正方形
∴AD＝AB，∠B＝∠BAD＝90°
∵AQ⊥DP
∴∠QAD＋∠ADP＝90°，且∠DAQ＋∠BAQ＝90°，
∴∠BAQ＝∠ADP，且∠B＝∠BAD＝90°，AD＝AB
∴△ABQ≌△DAP（ASA）
∴AP＝BQ
∴2t＝8−t
∴t＝，
故答案为：．
【点拨】本题考查了全等三角形判定和性质，正方形的性质，一元一次方程的应用，证明△ABQ≌△DAP是本题的关键．
19．2
【分析】
平行四边形ADCE的对角线的交点是AC的中点O，当OD⊥AB时，OD最小，即DE最小，根据直角三角形勾股定理即可求解．
【详解】
解：如图


∵平行四边形ADCE的对角线的交点是AC的中点O，又AB=AC=4
∴OC=OA=AC=2
当OD⊥AB时，OD最小，即DE最小．
∵OD⊥BA，∠BAC=45°，
∴∠AOD=45°
∴△ADO为等腰直角三角形
在Rt△ADO由勾股定理可知
OD= AO=
∴DE=2OD=2
故答案为：2．
【点拨】本题考查了勾股定理，平行四边形的性质，即平行四边形对角线互相平分，正确理解DE最小值的条件是关键．
20．4 2或
【分析】
（1）由已知得CH⊥AB，CH，BC已知，由勾股定理可求BH，由AB已知，故AH=AB-HB即可，
（2）由点P在折线DC—CH上运动，△PBC是等腰三角形，分两种情况，点P在DC上，当CP=BC时即可，点P在CH上，在Rt△BHP中，用勾股定理可求．
【详解】
（1）∵CH⊥AB于点H，CH=4， BC=5，
由勾股定理得CH2+BH2=BC2，BH=，
∵AB=7，
AH=AB-BH=7-3=4，
（2） 点P从点D出发， 以每秒1个单位长度的速度沿DC-CH向点H运动，到点H停止
①当点P在DC上时，△PBC是等腰三角形，由于BP>PC，BP>BC，只有当CP=BC时，满足条件，DP=t，∵四边形ABCD为平行四边形，∴DC=AB=7，PC=DC-DP=7-t，即7-t=5，t=2，

②当点P在CH上时，PC 综合上述得△PBC是等腰三角形时，t的值为2或．

故答案为：①4，②2或
【点拨】本题考查线段的长与确定等腰三角形问题，掌握平行四边形的性质，勾股定理，等腰三角形的性质，用t表示线段的长是解题关键．
21．
【分析】
由对称的性质和菱形的定义证出四边形AEGF是菱形，得出∠EAF=2∠BAC=120°，当AD⊥BC最小时，AD的值最小，即AE的值最小，即菱形AEGF面积最小，求出AD=，即可得出四边形AEGF的面积的最小值．
【详解】
解：由对称的性质得：AE=AD=AF，
∵四边形AEGF是平行四边形，
∴四边形AEGF是菱形，
∴∠EAF=2∠BAC=120°，
当AD⊥BC最小时，AD的值最小，即AE的值最小，即菱形AEGF面积最小，
∵∠ABC=45°，AB=2，
∴AD=，
∴四边形AEGF的面积的最小值=．
故答案为：．
【点拨】本题考查了平行四边形的性质、菱形的判定与性质、对称的性质；熟练掌握平行四边形的性质，证明四边形是菱形是解决问题的关键．
22．16或
【分析】
根据翻折的性质，可得B’E的长，根据勾股定理可得CE的长，然后再根据等腰三角形的判定进行分情况讨论．
【详解】
解：在正方形ABCD中，DC=16，若恰为等腰三角形，需分三种情况讨论：
（1）若，如图，

则（易知此时点在上且不与点、重合）；
（2）若，如图，

因为，，
所以点、在的垂直平分线上，则垂直平分，由折叠可知点与点重合，不符合题意，则这种情况不成立；
（3）如图，


若，作与交于点，交于点．
因为，
；
，
，
，
，
，
在中， ，
，
在中， ，
综上，或．
【点拨】本题考查了翻折变换的性质、正方形的性质、勾股定理等知识；熟练掌握翻折变换的性质和勾股定理是解题关键．
23．3或
【分析】
由四边形ABCD是平行四边形得出：AD∥BC，AD=BC，∠ADB=∠CBD，证得FB=FD，求出AD的长，得出CE的长，设当点P运动t秒时，点P、Q、E、F为顶点的四边形是平行四边形，根据题意列出方程并解方程即可得出结果．
【详解】
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠ADB=∠CBD，
∵∠FBD=∠CBD，
∴∠FBD=∠FDB，
∴FB=FD=11cm，
∵AF=5cm，
∴AD=16cm，
∵点E是BC的中点，
∴CE=BC=AD=8cm，
要使点P、Q、E、F为顶点的四边形是平行四边形，则PF=EQ即可，
设当点P运动t秒时，点P、Q、E、F为顶点的四边形是平行四边形，
分两种情况：①当点Q在EC上时，根据PF=EQ可得: 5-t=8-2t，
解得：t=3；
②当Q在BE上时，根据PF=QE可得：5-t=2t-8，
解得：t=．
所以，t的值为：t=3或t=．
故答案为：3或．
【点拨】本题考查了平行四边形的判定与性质、等腰三角形的判定与性质、一元一次方程的应用等知识，熟练掌握平行四边形的判定与性质是解决问题的关键．
24．2
【分析】
根据题意PD=t，则PA=10-t，首先证明BP=BC=10，在Rt△ABP中利用勾股定理即可解决问题，
【详解】
解：如图，根据题意PD=t，则PA=10−t，

∵B、E、P共线，
∴∠BPC=∠DPC，
∵AD∥BC，
∴∠DPC=∠PCB，
∴∠BPC=∠PCB，
∴BP=BC=10，
在Rt△ABP中，
∵，
∴，
∴t=2或18(舍去)，
∴PD=2，
∴t=2时，B、E、P共线；
故答案为：2.
【点拨】本题主要考查了矩形的性质，轴对称的性质，掌握矩形的性质，轴对称的性质是解题的关键.
25．2或2或．
【分析】
分两种情况：（1）①当∠BPC＝90°时，作AM⊥BC于M，求出BM＝AB＝1，AM＝BM＝，由勾股定理求出AC，由勾股定理的逆定理证出△ABC是直角三角形，∠BAC＝90°，得出点P与A重合即可；②当∠BPC＝90°，点P在边AD上，CP＝CD＝AB＝2时，由勾股定理求出BP即可；

（2）当∠BCP＝90°时，CP＝AM＝，由勾股定理求出BP即可．
【详解】
解：分两种情况：
（1）①当∠BPC＝90°时，
作AM⊥BC于M，如图1所示，
∵∠B＝60°，
∴∠BAM＝30°，
∴BM＝AB＝1，
∴AM＝BM＝，CM＝BC﹣BM＝4﹣1＝3，
∴AC＝＝2，
∴AB2+AC2＝BC2，
∴△ABC是直角三角形，∠BAC＝90°，
∴当点P与A重合时，∠BPC＝∠BAC＝90°，
∴BP＝BA＝2；
②当∠BPC＝90°，
点P在边AD上，CP＝CD＝AB＝2时，
BP＝＝＝2；
（2）当∠BCP＝90°时，如图3所示：
则CP＝AM＝，
∴BP＝＝；
综上所述：当△PBC为直角三角形时，BP的长为2或2或．
故答案为：2或2或．

【点拨】本题考查了平行四边形的动点问题，掌握平行四边形的性质、勾股定理是解题的关键．
26．（1）；（2）y＝S四边形ABPQ＝2t＋32（0＜t≤8）；（3）t＝8，；（4）当t＝4或 或时，为等腰三角形，理由见解析．
【分析】
（1）利用平行四边形的对边相等AQ＝BP建立方程求解即可；
（2）先构造直角三角形，求出AE，再用梯形的面积公式即可得出结论；
（3）利用面积关系求出t，即可求出DQ，进而判断出DQ＝PQ，即可得出结论；
（4）分三种情况，利用等腰三角形的性质，两腰相等建立方程求解即可得出结论．
【详解】
解：（1）∵在平行四边形中，，，
由运动知，AQ＝16−t，BP＝2t，
∵四边形ABPQ为平行四边形，
∴AQ＝BP，
∴16−t＝2t
∴t＝，
即：t＝s时，四边形ABPQ是平行四边形；
（2）过点A作AE⊥BC于E，如图，

在Rt△ABE中，∠B＝30°，AB＝8，
∴AE＝4，
由运动知，BP＝2t，DQ＝t，
∵四边形ABCD是平行四边形，
∴AD＝BC＝16，
∴AQ＝16−t，
∴y＝S四边形ABPQ＝（BP＋AQ）•AE＝（2t＋16−t）×4＝2t＋32（0＜t≤8）；
（3）由（2）知，AE＝4，
∵BC＝16，
∴S四边形ABCD＝16×4＝64，
由（2）知，y＝S四边形ABPQ＝2t＋32（0＜t≤8），
∵四边形ABPQ的面积是四边形ABCD的面积的四分之三
∴2t＋32＝×64，
∴t＝8；
如图，


当t＝8时，点P和点C重合，DQ＝8，
∵CD＝AB＝8，
∴DP＝DQ，
∴∠DQC＝∠DPQ，
∴∠D＝∠B＝30°，
∴∠DQP＝75°；
（4）①当AB＝BP时，BP＝8，
即2t＝8，t＝4；
②当AP＝BP时，如图，

∵∠B＝30°，
过P作PM垂直于AB，垂足为点M，
∴BM＝4，，
解得：BP＝，
∴2t＝，
∴t＝
③当AB＝AP时，同（2）的方法得，BP＝，
∴2t＝，
∴t＝
所以，当t＝4或 或时，△ABP为等腰三角形．
【点拨】此题是四边形综合题，主要考查了平行四边形的性质，含30°的直角三角形的性质，等腰三角形的性质，解（1）的关键是利用AQ＝BP建立方程，解（2）的关键是求出梯形的高，解（3）的关键是求出t，解（4）的关键是分类讨论的思想思考问题．
27．（1）24；（2）1或11；（3）t的值为2或6或10.8秒．
【分析】
（1）直接运用直角三角形面积等于两条直角边乘积的一半计算即可；
（2）分①当点P在AB边上时，②当点P在CD边上时，讨论即可；
（3）分①当点P在AB边上时，②当点P在BC边上时，③当点P在CD边上时，讨论S1与S2的大小即可求解 ．
【详解】
解：（1）∵点P从A点出发沿A-B-C-D移动，且点P的速度是2cm/s，t=2，
∴cm，
∵ cm，
∴S1 = cm2；
（2）当S1=12cm2时，有两种情况 ，
①当点P在AB边上时，如下图：

则S1=，解得： ，
∴t=，
②当点P在CD边上时，如下图：

则S1=，解得：
∴，
∴点P运动的路程为 ,
∴，
故：则t=1或11秒；
（3）①当点P在AB边上时，如下图：

S1 =，S2 =，显然S1>S2,
当|S1－S2|=18时，则9t=18,t1=2；
②当点P在BC边上时，如下图：

S1 =，S2 =，显然S1>S2,
当|S1－S2|=18时，则36-3t=18，t2=6；
③当点P在CD边上时，如下图：

S1 = ，S2 =，
此时无法判断S1与S2的大小,
当S1－S2=18时，则144-12t-3t=18,t3=8.4（舍去）
当S2－S1=18时，则3t-（144-12t）=18,t4=10.8
答：t的值为2或6或10.8秒．
【点拨】本题是三角形综合题，考查矩形的性质，三角形面积，绝对值的性质等知识，解题关键是运用分类讨论的思想．
28．（1）见解析；（2）能，当时，四边形AEFD为菱形；（3）当秒或4秒时，△DEF为直角三角形．
【分析】
（1）利用已知用未知数表示出DF，AE的长，进而得出AE＝DF；
（2）首先得出四边形AEFD为平行四边形，进而利用菱形的判定与性质得出AE＝AD时，求出t的值，进而得出答案；
（3）分三种情况讨论：①当∠EDF＝90°时；②当∠DEF＝90°时；③当∠EFD＝90°时，分别分析得出即可．
【详解】
解：（1）在△DFC中，∠DFC＝90°，∠C＝30°，DC＝2t，
∴DF＝CD＝t．
又∵AE＝t，
∴AE＝DF．
（2）四边形AEFD能够成为菱形．理由如下：
∵∠B＝90°，∠C＝30°，
∴AC＝2AB＝10．
由勾股定理得，BC＝5，
∴AB＝5，AC＝10．
∴AD＝AC﹣DC＝10﹣2t．
∵AB⊥BC，DF⊥BC，
∴AE∥DF．
又∵AE＝DF，
∴四边形AEFD为平行四边形．
若使四边形AEFD为菱形，则需AE＝AD，
即t＝10﹣2t，
解得：．
即当时，四边形AEFD为菱形．
（3）当秒或4秒时，△DEF为直角三角形，理由如下：
分情况讨论：
当∠EDF＝90°时，AD＝2AE，即10﹣2t＝2t，
∴．
②∠DEF＝90°时，
四边形AEFD为平行四边形．
则
AD＝AE，即10﹣2t＝t，
∴t＝4．
③∠EFD＝90°时，此种情况不存在．
故当秒或4秒时，△DEF为直角三角形．
【点拨】本题主要考查了平行四边形的判定、菱形的判定与性质、勾股定理、直角三角形的性质等知识，在直角三角形中，30°角所对的直角边等于斜边的一半．解题关键是熟练掌握相关知识．