浙江省金华十校2021-2022学年高一上学期期末联考数学试题

金华十校2021—2022学年第一学期期末调研考试

高一数学试题卷

一､选择题：本题共8小题，每小题5分，共40分在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合，，则（    ）

A.  B.  C.  D.

【答案】D

2. 命题：，命题：（其中），那么是的（    ）

A. 充分不必要条件 B. 必要不充分条件

C. 充要条件 D. 既不充分也不必要条件

【答案】A

3. 青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，小数记录法的数据V和五分记录法的数据L满足，已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据约为（    ）（注：）

A. 0.6 B. 0.8 C. 1.2 D. 1.5

【答案】B

4. 刘徽(约公元225年—295年)，魏晋期间伟大的数学家，中国古典数学理论的奠基人之一.他在割圆术中提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”，这可视为中国古代极限观念的佳作，割圆术的核心思想是将一个圆的内接正边形等分成个等腰三角形(如图所示)，当变得很大时，这n个等腰三角形的面积之和近似等于圆的面积，运用割圆术的思想，可以得到的近似值为（    ）

A.  B.  C.  D.

【答案】B

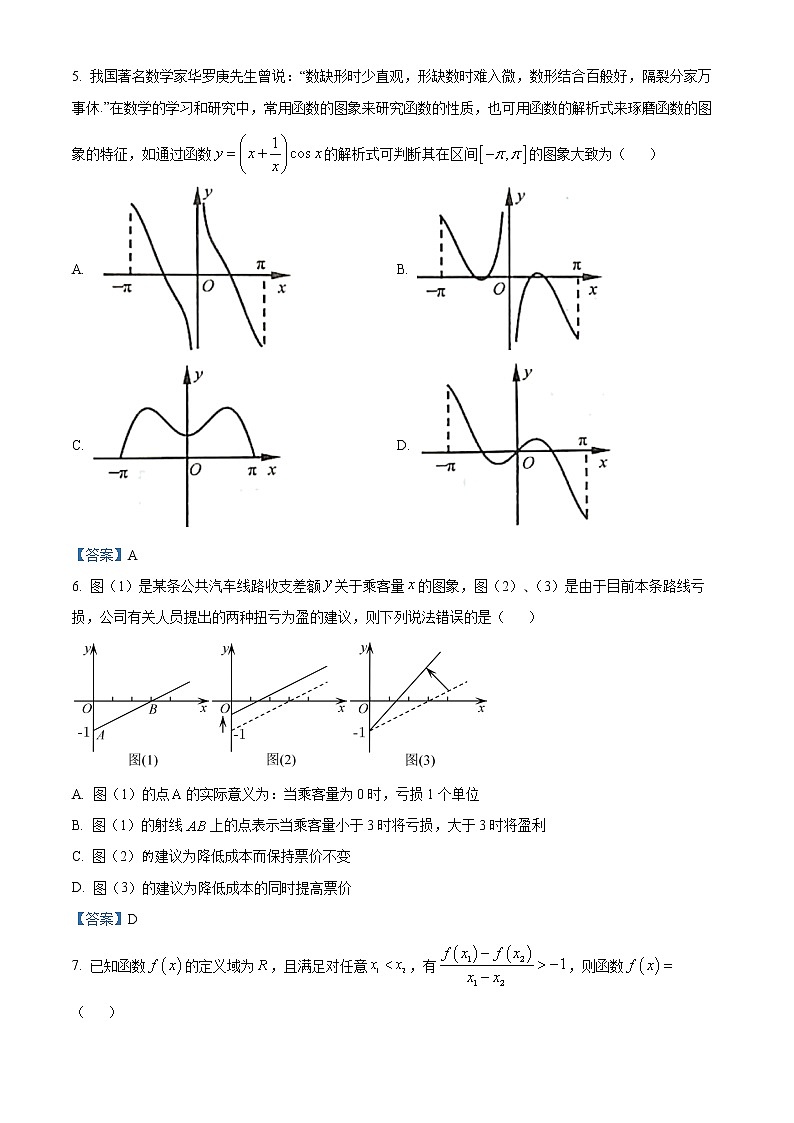
5. 我国著名数学家华罗庚先生曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休.”在数学的学习和研究中，常用函数的图象来研究函数的性质，也可用函数的解析式来琢磨函数的图象的特征，如通过函数的解析式可判断其在区间的图象大致为（    ）

A.  B.

C.  D.

【答案】A

6. 图（1）是某条公共汽车线路收支差额关于乘客量的图象，图（2）､（3）是由于目前本条路线亏损，公司有关人员提出的两种扭亏为盈的建议，则下列说法错误的是（    ）

A. 图（1）的点的实际意义为：当乘客量为0时，亏损1个单位

B. 图（1）的射线上的点表示当乘客量小于3时将亏损，大于3时将盈利

C. 图（2）建议为降低成本而保持票价不变

D. 图（3）的建议为降低成本的同时提高票价

【答案】D

7. 已知函数的定义域为，且满足对任意，有，则函数（    ）

A.  B.  C.  D.

【答案】C

8. 已知函数，若正数，，满足，则（    ）

A.

B.

C

D.

【答案】B

二､多选题：本题共4小题，每小题5分，共20分，在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.

9. 已知，，下列说法正确的有（    ）

A. 为奇函数 B. 在上单调递增

C.  D. 的图象关于对称

【答案】AC

10. 已知关于的不等式的解集为或，则下列说法正确的是（    ）

A

B. 的解集为

C

D. 解集为

【答案】AD

11. 已知，都是定义在上的函数，其中是奇函数，为偶函数，且，则下列说法正确的是（    ）

A. 为偶函数

B.

C. 为定值

D.

【答案】ACD

12. 已知二次函数，若，，，则的根的分布情况可能为（    ）

A. 可能无解

B. 有两相等解，且

C. 有两个不同解

D. 有两个都不在内的不同解，

【答案】ABC

三､填空题：本题共4小题，每小题5分，共20分.

13. 亲爱的考生，我们数学考试完整的时间是2小时，则从考试开始到结束，钟表的分针转过的弧度数为___________.

【答案】

14. 以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形.勒洛三角形是由德国机械工程专家、机构运动学家勒洛首先发现，所以以他的名字命名.一些地方的市政检修井盖、方孔转机等都有应用勒洛三角形.如图，已知某勒洛三角形的一段弧的长度为，则该勒洛三角形的面积是___________.

【答案】

15. 已知关于的不等式的解集为，其中，则的最小值是___________.

【答案】

16. 若在内无零点，则的取值范围为___________.

【答案】

四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.

17. 已知函数，

（1）求函数的最大值；

（2）若，，求的值

【答案】（1）3    （2）

18. 计算下列各式：

（1）

（2）

【答案】（1）；   

（2）.

19. 已知函数（其中，，）图象上两相邻最高点之间的距离为，且点是该函数图象上的一个最高点

（1）求函数的解析式；

（2）把函数的图象向右平移个单位长度，得到函数的图象，若恒有，求实数的最小值.

【答案】（1）   

（2）的最小值为4

20. 2015年10月，实施了30多年的独生子女政策正式宣告终结，党的十八届五中全会公报宣布在我国全面放开二胎政策.2021年5月31日，中共中央政治局召开会议，会议指出进一步优化生育政策，实施一对夫妻可以生育三个子女政策及配套支持措施，有利于改善我国人口结构，落实积极应对人口老龄化国家战略，保持我国人力资源禀赋优势.某镇2021年1月，2月，3月新生儿的人数分别为52，61，68，当年4月初我们选择新生儿人数和月份之间的下列两个函数关系式① ；②（，，，，都是常数），对2021年新生儿人数进行了预测.

（1）请你利用所给的1月，2月，3月份数据，求出这两个函数表达式；

（2）结果该地在4月，5月，6月份的新生儿人数是74，78，83，你认为哪个函数模型更符合实际？并说明理由.（参考数据：，，，，）

【答案】（1），   

（2）函数② 更符合实际，理由见解析

21. 己知函数，

（1）求在上的最小值；

（2）记集合，，若，求的取值范围.

【答案】（1）答案见解析   

（2）

22. 已知且是上的奇函数，且

（1）求的解析式；

（2）若不等式对恒成立，求的取值范围；

（3）把区间等分成份，记等分点的横坐标依次为，，设，记，是否存在正整数，使不等式有解？若存在，求出所有的值，若不存在，说明理由.

【答案】（1）；   

（2）；   

（3）存在，正整数或2.