2023届中考数学高频考点专项练习：专题十五 圆综合训练（B）

这是一份2023届中考数学高频考点专项练习：专题十五 圆综合训练（B），共13页。
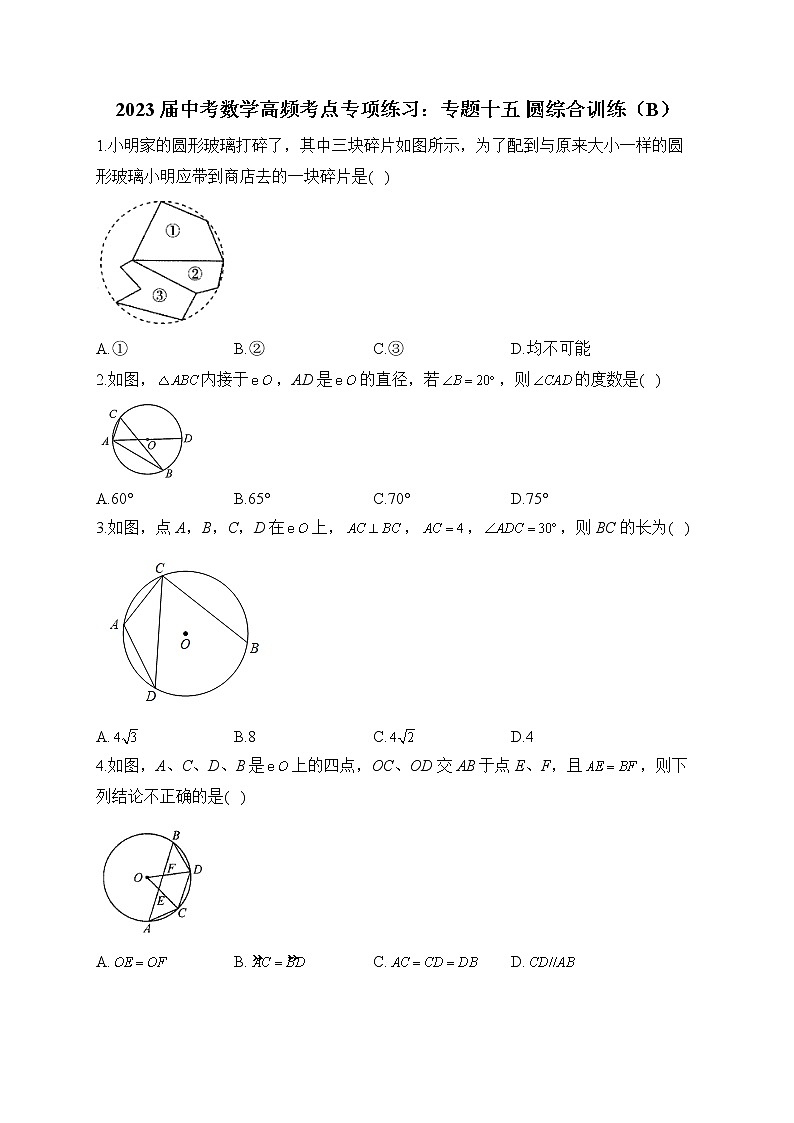
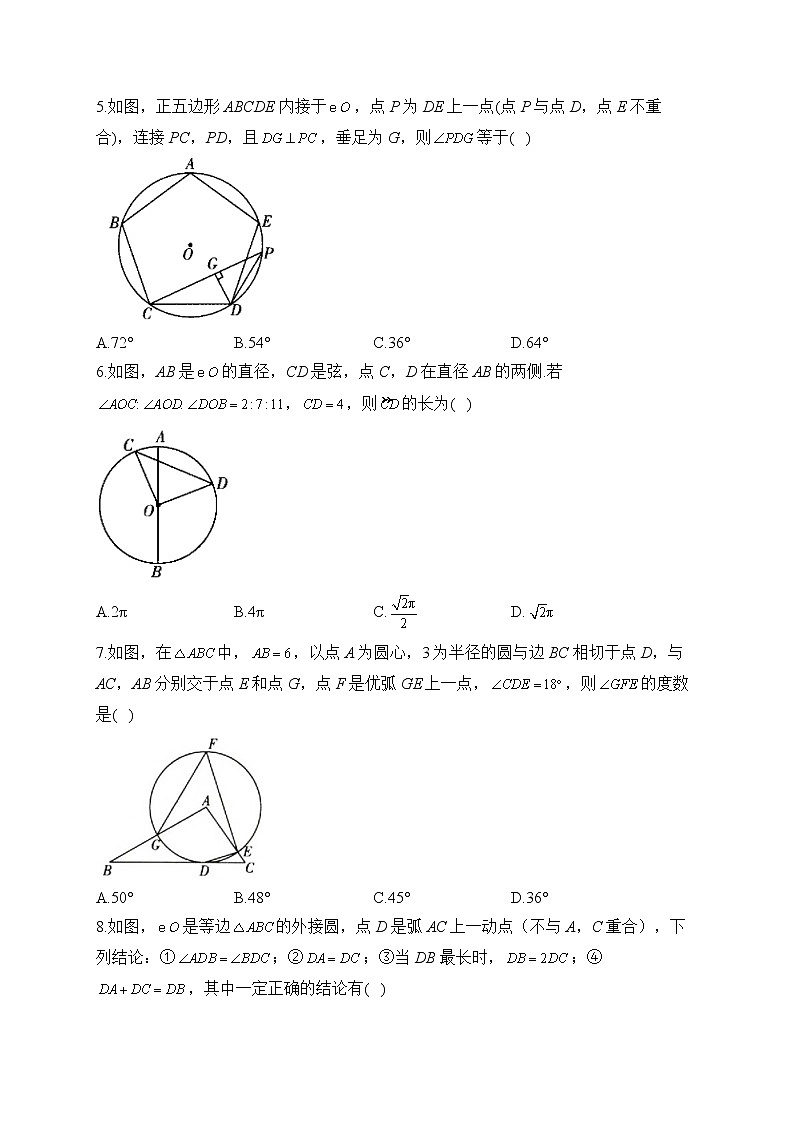
2023届中考数学高频考点专项练习：专题十五 圆综合训练（B）1.小明家的圆形玻璃打碎了，其中三块碎片如图所示，为了配到与原来大小一样的圆形玻璃小明应带到商店去的一块碎片是(   )A.① B.② C.③ D.均不可能2.如图，内接于，AD是的直径，若，则的度数是(   )A.60° B.65° C.70° D.75°3.如图，点A，B，C，D在上，，，，则BC的长为(   )A. B.8 C. D.44.如图，A、C、D、B是上的四点，OC、OD交AB于点E、F，且，则下列结论不正确的是(   )A. B. C. D.5.如图，正五边形ABCDE内接于，点P为DE上一点(点P与点D，点E不重合)，连接PC，PD，且，垂足为G，则等于(   )A.72° B.54° C.36° D.64°6.如图，AB是的直径，CD是弦，点C，D在直径AB的两侧.若，，则的长为(   )A.2π B.4π C. D.7.如图，在中，，以点A为圆心，3为半径的圆与边BC相切于点D，与AC，AB分别交于点E和点G，点F是优弧GE上一点，，则的度数是(   )
 A.50° B.48° C.45° D.36°8.如图，是等边的外接圆，点D是弧AC上一动点（不与A，C重合），下列结论：①；②；③当DB最长时，；④，其中一定正确的结论有(   )A.1个 B.2个 C.3个 D.4个9.如图，AB是的直径，将弦AC绕点A顺时针旋转30°得到AD，此时点C的对应点D落在AB上，延长CD，交于点E，若，则图中阴影部分的面积为(   )A. B. C. D.10.如图所示，已知三角形ABE为直角三角形，，BC为圆O切线，C为切点，，则和面积之比为(   )A. B. C. D.11.如图所示，点A是半圆上一个三等分点，点B是的中点，点P是直径MN上一动点，若的直径为2，则的最小值是____________.12.如图，是半圆O的直径，点D是半圆上一点，过点D作的切线于点交半圆于点E.已知，那么直线与以点O为圆心，3为半径的圆的位置关系是__________.13.如图，在扇形AOB中，点C，D在上，将沿弦CD折叠后恰好与OA，OB相切于点E，F.已知，，则的度数为_______；折痕CD的长为_______.14.如图，正方形ABCD的边长为4，M为AB的中点，P是BC边上的动点，连接PM，以点P为圆心，PM长为半径作圆P，当圆P与正方形ABCD的边相切时，CP的长为____________.15.如图，是的外接圆，O点在BC边上，的平分线交于点D，连接BD、CD，过点D作BC的平行线，与AB的延长线相交于点P.（1）求证：PD是的切线；（2）求证：；（3）当，时，求线段PB的长.
答案以及解析1.答案：A解析：碎片①中有不在同一条直线上的三点在圆形玻璃上，可以确定一个圆，即可以配到与原来大小一样的圆形玻璃.故选A2.答案：C解析：解法一：连接BD.AD是的直径，.又，，.解法二：连接OC，则，.，，.3.答案：A解析：连接AB，如图所示，
 ，.，.在中，，.，.故选：A.4.答案：C解析：连接OA，OB，如图，，.在与中，，（A选项正确），，即，（B选项正确）.连接AD，，，（D选项正确）.故选C.5.答案：B解析：如图，连接OC，OD.在正五边形ABCDE中，，.，，.6.答案：D解析：，，，，，.在中，，，，，的长是.故选D.7.答案：B解析：如图，连接AD，与相切，.，，，.，.又，，，，.故选B.
 8.答案：C解析：是等边三角形，，，，，，，故①正确；点D是弧AC上一动点，与不一定相等，DA与DC不一定相等，故②错误；当DB最长时，DB为直径，，，，，故③正确；在DB上取一点E，使，如图：，是等边三角形，，，，，，，，，故④正确；正确的有①③④，共3个，故选：C.9.答案：C解析：连接OE，OC，BC，由旋转知，，，，，，，即为等腰直角三角形，，，，故选：C.10.答案：B解析：解：如图取DE中点O，连接OC.
 DE是圆O的直径.
.
BC与圆O相切.
.
.
.
.
.
又.
.
，，.
.
.
点O是DE的中点.
.
.
.
故答案是：.故选：B.11.答案：解析：作点B关于MN的对称点，连接交MN于点P，连接BP，由三角形两边之和大于第三边，即可得出此时最小，连接，根据点A是半圆上一个三等分点、点B是的中点，即可得出，再利用勾股定理即可求出的值，此题得解.12.答案：相切解析：如图，连接交于点F，则.是半圆O的直径，，.又，四边形是矩形，，.在中，，直线与以点O为圆心，3为半径的圆的位置关系是相切.13.答案：60°，解析：作O关于CD的对称点M，则，连接MD、ME、MF、MO，MO交CD于N将沿弦CD折叠
点D、E、F、B都在以M为圆心，半径为6的圆上
将沿弦CD折叠后恰好与OA，OB相切于点E，F.
，


四边形MEOF中即的度数为60°；
，，
，
，
，
，
，
，
，故答案为：60°；.14.答案：2.5或解析：如图（1），当与CD相切时，设，则.M为AB的中点，.在中，，，，.如图（2），当与AD相切时.设切点为K，连接PK，则，四边形PKDC是矩形..，.在中，，.综上所述，CP的长为2.5或.故答案是2.5或.15.答案：（1）见解析（2）见解析（3）解析：（1）证明：连接OD，如图，AD是的角平分线，，，，，，PD是的切线；（2），，，，，，，，（3）如图，连接OD，BC是的直径，，，在中，，，，，，在中，，，，即，.