
专题 19.3 变量与函数(巩固篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版)
展开专题 19.3 变量与函数(巩固篇)(专项练习)
一、 单选题
知识点一、函数概念
1.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器的容积
2.下列图象中,表示y是x的函数的是( )
A. B. C. D.
3.下列式子:①y=3x﹣5;②y=;③y=;④y2=x;⑤y=|x|,其中y是x的函数的个数是( )
A.2个 B.3个 C.4个 D.5个
知识点二、函数解析式
4.如果一盒圆珠笔有12支,售价18元,用(元)表示圆珠笔的售价,表示圆珠笔的支数,那么与之间的解析式为( ).
A. B. C. D.
5.等腰三角形的周长为36,腰长为x,底边长为y,则下列y与x的关系式及自变量x的取值范围中,正确的是( )
A.y=36﹣x(0<x<36) B.y=36﹣x(0<x<18)
C.y=36﹣2x(0<x<18) D.y=36﹣2x(9<x<18)
6.如图,y与x之间的关系式为( )
A.y=x+60 B.y=x+120 C.x=60+y D.y=30+x
知识点三、函数自变量的取值范围
7.若有意义,则x的取值范围是
A.且 B. C. D.
8.函数y=中,自变量x的取值范围在数轴上表示正确的是( )
A. B. C. D.
9.下列说法中正确的是( )
A.8的立方根是±2
B.是一个最简二次根式
C.函数的自变量x的取值范围是x>1
D.在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称
知识点四、求函数自变量的值或函数值
10.已知函数,其中表示时的函数值,则的值为( )
A.2020 B.2021 C.4040 D.4041
11.结合学习函数的经验,小红在平面直角坐标系中画出了函数的图象,如图所示.根据图象,小红得到了该函数四条结论,其中正确的是( )
A.y随x的增大而减小 B.当时,y有最大值
C.当与时,函数值相等 D.当时,
12.若函数,则当函数值y=8时,自变量x的值是( )
A.± B.4 C.±或4 D.4或-
知识点五、表格法表示函数关系
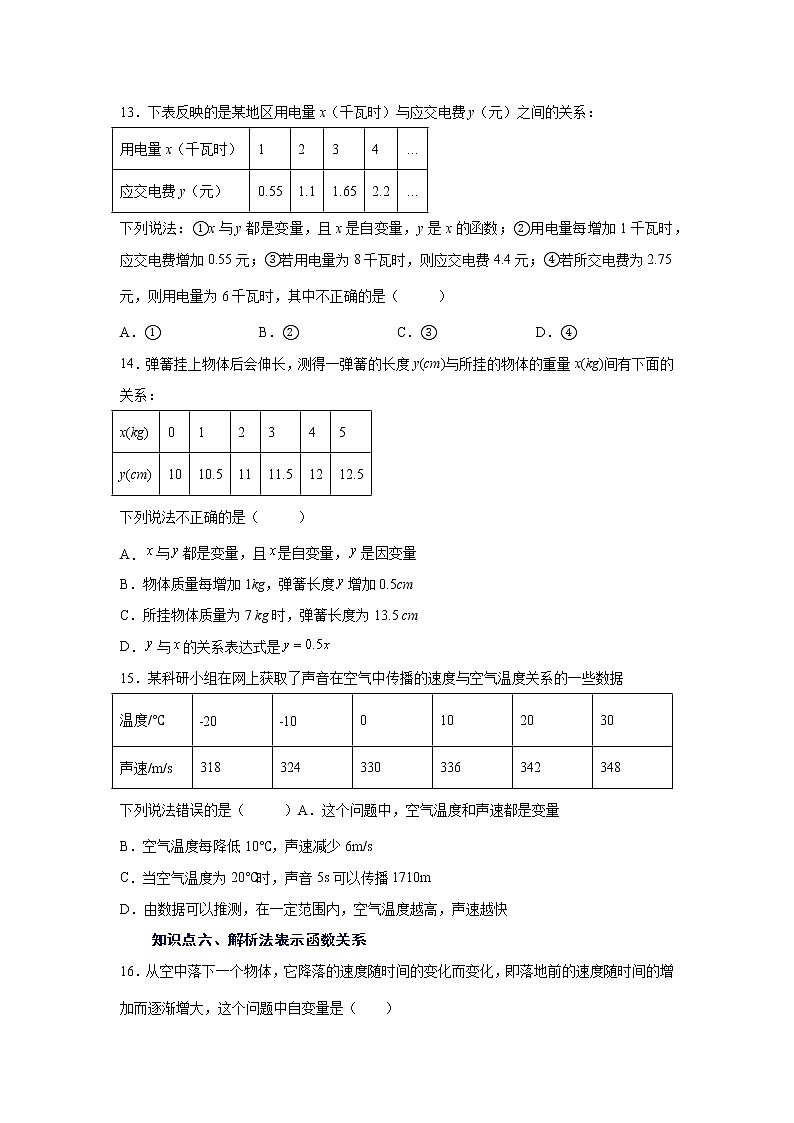
13.下表反映的是某地区用电量x(千瓦时)与应交电费y(元)之间的关系:
用电量x(千瓦时)
1
2
3
4
…
应交电费y(元)
0.55
1.1
1.65
2.2
…
下列说法:①x与y都是变量,且x是自变量,y是x的函数;②用电量每增加1千瓦时,应交电费增加0.55元;③若用电量为8千瓦时,则应交电费4.4元;④若所交电费为2.75元,则用电量为6千瓦时,其中不正确的是( )
A.① B.② C.③ D.④
14.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
x(kg)
0
1
2
3
4
5
y(cm)
10
10.5
11
11.5
12
12.5
下列说法不正确的是( )
A. 与都是变量,且是自变量,是因变量
B.物体质量每增加1kg,弹簧长度增加0.5cm
C.所挂物体质量为7 kg时,弹簧长度为13.5 cm
D.与的关系表达式是
15.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据
温度/℃
﹣20
﹣10
0
10
20
30
声速/m/s
318
324
330
336
342
348
下列说法错误的是( )A.这个问题中,空气温度和声速都是变量
B.空气温度每降低10℃,声速减少6m/s
C.当空气温度为20℃时,声音5s可以传播1710m
D.由数据可以推测,在一定范围内,空气温度越高,声速越快
知识点六、解析法表示函数关系
16.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前的速度随时间的增加而逐渐增大,这个问题中自变量是( )
A.物体 B.速度 C.时间 D.空气
17.在圆的面积计算公式,其中为圆的半径,则变量是( )
A. B. C., D.,
18.在△ABC中,若底边长是a,底边上的高为h,则△ABC的面积,当高h为定值时,下列说法正确的是( )
A.S,a是变量;,h是常量
B.S,a,h是变量;是常量
C.a,h是变量;S是常量
D.S是变量;,a,h是常量
知识点七、图象法表示函数关系
19.是饮水机的图片.饮水桶中的水由图1的位置下降到图2的位置的过程中,如果水减少的体积是y,水位下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )
A. B. C. D.
20.小明带了2元钱去买笔,每支笔的价格是0.5元,那么小明买完笔后剩下的钱数y(元)与买到的笔的数量x(支)之间的函数图象大致是( ).
A. B.
C. D.
21.小慧今天到学校参加初中毕业会考,从家里出发走10分钟到离家500米的地方吃早餐,吃早餐用了20分钟;再用10分钟赶到离家1000米的学校参加考试.下列图象中,能反映这一过程的是( )
A. B.
C. D.
22.为积极响应党和国家精准扶贫的号召,某扶贫工作队步行前往扶贫点开展入户调查。队员们先匀速步行一段时间,途中休息几分钟后加快了步行速度,最终按原计划时间到达目的地。设行进时间为t(单位:min),行进的路程为s(单位:m),则能近似刻画s与t之间的函数关系的大致图象是( )
A.B.C.D.
二、填空题
知识点一、函数概念
23.下列是关于变量x与y的八个关系式:① y = x;② y2 = x;③ 2x2 − y = 0;④ 2x − y2 = 0;⑤ y = x3 ;⑥ y =∣x∣;⑦ x = ∣y∣;⑧ x =.其中y不是x的函数的有_____.(填序号)
24.下列变量间的关系是函数关系的有_____________________(填序号)
①正方形的周长与边长;②圆的面积与半径;
③;④商场中某种商品的单价为a元,销售总额与销售数量
25.将写成用的代数式表示的形式为______,那么______是______的函数,______是自变量.
知识点二、函数解析式
26.用每片长6cm的纸条,重叠1cm粘贴成一条纸带,如图.纸带的长度y(cm)与纸片的张数x之间的函数关系式是___________________
27.汽车开始行驶时,油箱中有油40升,如果每小时耗油5升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为_____,该汽车最多可行驶_____小时.
28.如图所示每个图形是由若干个花盆组成的三角形的图案,每条边(包括顶点)有n(n>1)盆花,每个图案共有s盆花,则s与n之间的关系式为______ .
知识点三、函数自变量的取值范围
29.函数中自变量x的取值范围是______.
30.在函数中,自变量x的取值范围是_________.
31.函数中,自变量x的取值范围是___.
知识点四、求函数自变量的值或函数值
32.对于正数,规定 ,例如:,,则f(2013)+f(2012)+…+…=_____________.
33.若对于所有的实数,都有,则______.
34.已知M=﹣x+3,当x分别取1,2,3,…,2020时,所对应M值的总和是_____.
知识点五、表格法表示函数关系
35.声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下:
从表中可知音速y随温度x的升高而_____.在气温为20 ℃的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点________米.
36.如果用总长为60m的篱笆围成一个长方形场地,设长方形的面积为,一边长为,那么在60,s,a中,变量有________________个.
37.下面的表格列出了一个实验的统计数据,表示将皮球从高处落下时,弹跳高度与下降高度的关系,则弹跳高度与下降高度的函数解析式为______.
50
80
100
150
25
40
50
75
知识点六、解析法表示函数关系
38. 如图,在长方形ABCD中,AB=CD=5厘米,AD=BC=4厘米. 动点P从A出发,以1厘米/秒的速度沿A→B运动,到B点停止运动;同时点Q从C点出发,以2厘米/秒的速度沿C→B→A运动,到A点停止运动.设P点运动的时间为t秒(t > 0),当t=____________时,S△ADP=S△BQD.
知识点七、图象法表示函数关系
39.快餐每盒5元,买n盒需付m元,则其中常量是_____.
40.一种豆子在市场上出售,豆子的总售价与所售豆子的数量之间的关系如下表:
所售豆子数量/千克
0
0.5
1
1.5
2
2.5
3
3.5
4
总售价/元
0
1
2
3
4
5
6
7
8
(1)上表反映的变量是____________,________是因变量,______随____________的变化而变化;
(2)若出售2.5千克豆子,则总售价应为________元;
(3)根据你的预测,出售________千克豆子,可得总售价12元.
41.如图所示,梯形的上底长是厘米,下底长是厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
()在这个变化过程中,自变量是__________,因变量是__________.
()梯形的面积与高(厘米)之间的关系式为__________.
()当梯形的高由厘米变化到厘米时,梯形的面积由__________变化到__________.
参考答案
1.B
【分析】
函数的定义:设在某变化过程中有两个变量、,如果对于在某一范围内的每一个确定的值,都有唯一的值与它对应,那么称是的函数,叫自变量.函数关系式中,某特定的数会随另一个(或另几个)会变动的数的变动而变动,就称为因变量.
解:根据函数的定义可知,
水温是随着所晒时间的长短而变化,
可知水温是因变量,
所晒时间为自变量.
故选:B.
【点拨】本题主要考查的是对函数的定义,解题的关键是对自变量和因变量的认识和理解.
2.D
【分析】
函数就是在一个变化过程中有两个变量x,y,当给x一个值时,y有唯一的值与其对应,就说y是x的函数,x是自变量.注意“y有唯一的值与其对应”对图象的影响.
根据函数的定义可知,每给定自变量x一个值都有唯一的函数值y相对应,
所以A、B、C错误.
故选D.
【点拨】主要考查了函数图象的读图能力.要能根据函数图象的性质和图象上的数据分析得出函数的知识点和所需要的条件,结合实际意义得到正确的结论.函数的意义反映在图象上简单的判断方法是:做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点.
3.C
【分析】
根据函数的定义逐一进行判断即可得.
①y=3x﹣5,y是x的函数;
②y=,y是x的函数;
③y=,y是x的函数;
④y2=x,当x取一个值时,有两个y值与之对应,故y不是x的函数;
⑤y=|x|,y是x的函数,
故选C.
【点拨】本题考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
4.A
【分析】
首先求出每支平均售价,即可得出y与x之间的关系.
∵每盒圆珠笔有12支,售价18元,
∴每只平均售价为:=1.5(元),
∴y与x之间的关系是:,
故选:A.
【点拨】此题主要考查了列函数关系式,求出圆珠笔的平均售价是解题关键.
5.D
【分析】
根据等腰三角形的周长公式得到x和y的关系式,再根据三角形三边关系求得x的取值范围即可.
解:∵等腰三角形的周长为36,腰长为x,底边长为y,
∴2x+y=36,
即y=36﹣2x,
∵y>0且2x>y,
∴36﹣2x>0,2x>36﹣2x,
解得:9<x<18,
∴y=36﹣2x(9<x<18),
故选:D.
【点拨】本题考查等腰三角形的性质、列函数关系式、三角形的三边关系、解一元一次不等式,解答的关键是根据等腰三角形的周长列出函数的解析式,熟练掌握三角形的三边关系.
6.A
【分析】
由三角形外角性质可得结论.
∵三角形一个外角等于与它不相邻的两个内角和,
∴y=x+60.
故选A.
【点拨】考查了三角形外角的性质,解题关键是运用三角形一个外角等于与它不相邻的两个内角和得出关系式.
7.A
【分析】
根据二次根式有意义的条件和分式有意义的条件即可求出答案.
由题意可知:,
解得:且,
故选A.
【点拨】本题考查了分式有意义的条件、二次根式有意义的条件,熟练掌握分式的分母不为0、二次根式的被开方数为非负数是解题的关键.
8.B
【分析】
根据函数y=可得出x-5≥0,再解出一元一次不等式即可.
由题意得,x-5≥0,
解得x≥5.
在数轴上表示如下:
故选B.
【点拨】本题要考查的是一元一次不等式的解法以及二次根式成立得出判定,熟练掌握一元一次不等式的解法是本题的解题关键.
9.D
试题分析:A.8的立方根是2,故A不符合题意;
B.不是最简二次根式,故B不符合题意;
C.函数的自变量x的取值范围是x≠1,故C不符合题意;
D.在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称,故D符合题意;
故选D.
考点:最简二次根式;立方根;函数自变量的取值范围;关于x轴、y轴对称的点的坐标.
10.D
【分析】
根据题意可得:,利用这种规律即可求解.
解:有题意可得:,
故选:D.
【点拨】本题考查函数值求和问题,解题的关键是:通过题意找到多项函数值中两项之和为常数,然后两两分为一组求和.
11.D
【分析】
根据函数的图象以及函数的解析式逐一判断即可.
A:由图象可知,当时,随的增大而增大,故本选项不合题意;
B:函数的自变量的取值范围为,故本选项不合题意;
C:当时,函数值为;当时,函数值为1,故本选项不合题意;
D:由图象可知,当时,,故本选项符合题意.
故选:D.
【点拨】本题考查了函数的图象和性质,解题关键是根据函数解析式得出函数值和自变量的取值范围.
12.D
把y=8代入第二个方程,解得x=4大于2,所以符合题意;
把y=8代入第一个方程,解得: x=,
又由于x小于等于2,所以x=舍去,
所以选D
13.D
【分析】
根据函数的定义判断①,通过表格求出应交电费与电量的变化规律求出每一千瓦时的电费,然后判断②③④三项即可.
解:①x与y都是变量,且x是自变量,y随x的变化而变化,故y是x的函数,此项正确;
②从表格可以看出,用电量每增加1千瓦时,电费增加0.55元,故此项正确;
③若用电量为8千瓦时,则应交电费元,故此项正确;
④若所交电费为2.75元,则用电量千瓦时,故此项不正确;
故选:D.
【点拨】本题考查了函数的相关知识,题目难度不大,根据图表列出函数关系是解决本题的关键.
14.D
【分析】
由表中的数据进行分析发现与满足一次函数关系,根据图表求出表达式,然后逐个分析四个选项,可得出最终结果.
根据图表观察与满足一次函数关系,
设,
代入(0,10)和(2,11)两点,
得:,
解得:,
y与x的关系表达式是y= 0.5x+ 10,
A、y随x的增加而增加,x是自变量,y是因变量,故A选项正确,不符合题意;
B、由图表知,物体质量每增加1kg,弹簧长度y增加0.5cm,故B选项正确,不符合题意;
C、由表达式知,当x= 7时,y = 13.5,即所挂物体质量为7kg时,弹簧长度为13.5cm,故C选项正确,不符合题意;
D、y与x的关系表达式是y= 0.5x+ 10,D选项错误,符合题意.
故选:D.
【点拨】本题考查了一次函数的概念,属于基础题,能够根据所给的表进行分析变量的值的变化情况,同时求出表达式是解题的关键.
15.B
【分析】
根据表格中两个变量的数据变化情况,逐项判断即可.
解:这个问题中,空气温度和声速都是变量,因此选项A不符合题意;
在一定的范围内,空气温度每降低10℃,声速减少6m/s,表格之外的数据就不一定有这样规律,因此选项B符合题意;
当空气温度为20℃时,声速为342m/s,声音5s可以传播342×5=1710m,因此选项C不符合题意;
从表格可得,在一定范围内,空气温度越高,声速越快,因此选项D不符合题意;
故选:B.
【点拨】本题考查变量之间的关系,理解自变量、因变量之间的变化关系是正确判断的前提.
16.C
【分析】
根据函数的定义解答.
解:因为速度随时间的变化而变化,
故时间是自变量,速度是因变量,
即速度是时间的函数.
故选C.
【点拨】本题考查了常量与变量,关键是掌握函数的定义:设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数.
17.D
【分析】
在圆的面积计算公式中,π是圆周率,是常数,变量为S,R.
在圆的面积计算公式中,π是圆周率,是常数,变量为S,R.
故选D.
【点拨】本题主要考查常量与变量,解题关键是熟练掌握圆的面积S随半径的变化而变化.
18.A
因为高h为定值,所以h是不变的量,即h是常量,所以S,a是变量,,h是常量.
故选A.
19.C
【分析】
水位随着水减少而下降,且饮水机是圆柱形,是同等变化的下降.
根据图片位置分析:水减少的体积随着水位下降的高度而增加,且饮水机是圆柱形,所以均匀增加
故答案选:C
【点拨】本题考查用图象法表示变量之间的关系,掌握变量之间的变化关系解题关键.
20.D
【分析】
根据题意列出函数解析式,进而根据实际意义求得函数图像,注意自变量的取值范围.
依题意,(为正整数)
可以取得,对应的的值为,
故选D
【点拨】本题考查了根据实际问题列出函数关系式,变量与函数图像,结合实际是解题的关键.
21.D
【分析】
根据小慧离家的距离是增加还是不变的关系看图象,进而做出判断.
解:小慧从家里出发走10分钟到离家500米的地方吃早餐,离家的距离在增加,吃早餐用了20分钟,离家的距离不变,再用10分钟赶到离家1000米的学校,离家的距离又在增加,且与开始快慢相同,参加考试后离家的距离不变,故D项符合题意.
【点拨】本题考查了用图象法表示变量之间的关系,正确理解题意与对应图象的关系是解题的关键.
22.A
【分析】
根据行进的路程和时间之间的关系,确定图象即可得到答案.
解:根据题意得,队员的行进路程s(单位:m)与行进时间t(单位:min)之间函数关系的大致图象是
故选:A
【点拨】本题考查函数图象,正确理解函数自变量与因变量的关系及其实际意义是解题的关键.
23.②④⑦
根据函数的定义:“在一个变化过程中,若有两个变量x、y,在一定的范围内当变量x每取定一个值时,变量y都有唯一确定的值和它对应,我们就说变量y是变量x的函数”分析可知,在上述反映变量y与x的关系式中,y不是x的函数的有②④⑦,共3个.
故答案为②④⑦.
24.①②④.
在一个变化过程中,有两个变量x和y,对于x的每一个确定值,y都有唯一的值与之对应,则称y是x的函数,在③中,当x取一个值时,对应的y值有两个,故不是函数,
故答案为①②④.
25.
【分析】
根据等式的性质将等式表示成左边为b右边为含a的代数式的形式即可,根据函数的定义填写后面三个空.
解:∵
移项可得:
将b的系数化为1得:.
根据函数的定义b是a的函数,a是自变量,b是因变量
故四个空依次填:,b,a,a.
【点拨】等式的性质和函数的定义.在用的代数式表示时可将a看成已知数,b看成未知数,解b的方程即可,理解函数的定义也是解决本题的关键.
26.y=5x+1.
【分析】
根据粘合后的总长度=x张纸条的长-(x-1)个粘合部分的长,列出函数解析式即可.
纸带的长度y(cm)与纸片的张数x之间的函数关系式是y=6x−(x−1)=5x+1,
故答案为y=5x+1.
【点拨】此题考查函数关系式,解题关键在于根据题意列出方程.
27. y=40﹣5x 8
【分析】
根据:油箱内余油量=原有的油量﹣x小时消耗的油量,可列出函数关系式,进而得出行驶的最大路程.
依题意得,油箱内余油量y(升)与行驶时间x(小时)的关系式为:y=40﹣5x,
当y=0时,40﹣5x=0,
解得:x=8,
即汽车最多可行驶8小时.
故答案为:y=40﹣5x,8.
【点拨】本题考查了列函数关系式以及代数式求值.关键是明确油箱内余油量,原有的油量,x小时消耗的油量,三者之间的数量关系,根据数量关系可列出函数关系式.
28.s=
【分析】
将n的值与s的值对应起来,找出规律,即可得出s与n的关系式.
解:n=1时,s=1+2=×(1+1)×(1+2)=3;
n=2时,s=1+2+3=×(2+1)×(2+2)=6;
n=3时,s=1+2+3+4=×(3+1)×(3+2)=10;
…
∴n=n时,s=.
故答案为s=.
【点拨】此题主要考查了函数关系式以及数字规律问题,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,进而解题.
29.
【分析】
根据二次根式及分式有意义的条件,结合所给式子得到关于x的不等式组,解不等式组即可求出x的取值范围.
由题意得,,
解得:-2
30.且
【分析】
根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
根据题意得:,
解得:且.
故答案为:且.
【点拨】本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.
31.x≥0且x≠2且x≠3
试题分析:求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数、分式分母不为0和0指数幂不为0的条件,要使在实数范围内有意义,必须且x≠2且x≠3.
32.
【分析】
由规定的计算可知,由此分组求得答案,再相加即可求解.
解:
.
故答案为:.
【点拨】本题考查了新定义运算,掌握规定的运算方法,运算中找出规律,利用规律,解决问题.
33.0
【分析】
令x=1和x=-1,得到①,②,两个等式相减,即可得到答案.
解:∵对于所有的实数,都有,
∴当x=1时,①,
当x=-1时,②,
①-②,得:,解得:0.
故答案是:0.
【点拨】本题主要考查抽象函数求值,掌握赋值法以及等式的性质,是解题的关键.
34.2022
【分析】
先化简二次根式求出y的表达式,再将x的取值依次代入,然后求和即可得.
解:M=﹣x+3=|x﹣2|﹣x+3,
①当x≤2时,|x﹣2|=2﹣x,此时M=﹣x+3=2﹣x﹣x+3=5﹣2x,
x=1,M=5﹣2x=3,
x=2,M=5﹣2x=1,
②当x>2时,|x﹣2|=x﹣2,此时M=﹣x+3=x﹣2﹣x+3=1,
∴当x分别取1,2,3,…,2020时, 所对应M的值和=3+1+1×(2020﹣2)=2022.
故答案为:2022.
【点拨】本题考查了二次根式的化简求值、绝对值运算等知识点,掌握二次根式的化简方法是解题关键.
35. 增大; 68.6.
【分析】
从表格可以看到y随x的增大而增大;20℃时,音速为343米/秒,距离为343×0.2=68.6米.
从表格可以看到y随x的增大而增大;
20℃时,音速为343米/秒,343×0.2=68.6米,
这个人距离发令点68.6米;
故答案为:增大;68.6.
【点拨】本题考查变量之间的关系,函数的表示方法;能够通过表格观察出变量的变化关系,利用表格的数据计算距离是解题的关键.
36.2
【分析】
根据篱笆的总长确定,即可得到周长、一边长及面积中的变量.
∵篱笆的总长为60米,
S=(30-a)a=30a-a2
∴面积S随一边长a变化而变化
S与a是变量,
故答案为:2.
【点拨】本题考查了常量与变量的知识,解题的关键是能够根据篱笆总长不变确定定值,然后确定变量
37.
【分析】
观察表格发现d都是b的2倍,直接写出解析式即可.
观察表格发现d都是b的2倍,则弹跳高度与下降高度的函数解析式为.
【点拨】本题对函数表格的考查,准确观察表格得出结论是解决本题的关键,难度较小.
38.s或4s
【分析】
分两种情况:(1)当点Q在CB上时,如图1所示,(2)当点Q运动至BA上时,如图2所示,分别根据三角形的面积公式即可列出关于t的方程,解方程即可.
解:分两种情况:(1)当点Q在CB上时,如图1所示:
S△ADP=AD×AP=2t,S△BQD=BQ×DC=(4﹣2t),
则2t=(4﹣2t),解得:t=;
(2)当点Q运动至BA上时,如图2所示:
S△ADP=AD×AP=2t,S△BQD=BQ×DA=2(2t﹣4),
则2t=2(2t﹣4),解得:t=4;
综上可得:当t=s或4s时,S△ADP=S△BQD.
故答案为:s或4s.
【点拨】本题主要考查了三角形的面积、变量之间的关系和简单的一元一次方程的解法,正确分类、善于动中取静、灵活应用运动变化的观点是解题的关键.
39.5
【分析】
根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量.
解:单价5元固定,是常量.
故答案为:5.
【点拨】考核知识点:函数.理解函数相关意义是关键.
40. 所售豆子数量和总售价 总售价 总售价 所售豆子数量 5 6
【分析】
根据表中数据,售价与所售数量成正比例关系.售价=所售豆子的数量×单价.
(1)表反映的变量是所售豆子数量和售价,售价是因变量,售价随所售豆子数量的变化而变化的;
(2)5;
(3)根据题意设解析式为y=kx,
则0.5k=1,
解得k=2,
∴y=2x,
当y=12时2x=12,
解得x=6.
故答案为所售豆子数量和总售价;总售价;总售价;所售豆子数量;5;6.
【点拨】函数的意义是本题考查的重点.明确变量及变量之间的关系是解好本题的关键.
41. 梯形的高 梯形的面积 90 9
【分析】
(1)在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据梯形的面积公式(上底+下底)×高÷2,代入相应数值,进行计算即可;
(3)把x=10,x=1分别代入函数解析式进行计算.
解:(1)自变量是梯形的高,因变量是梯形的面积;
(2)梯形的面积y(cm²)与高x(cm)之间的关系式为:y=(5+13)x×=9x;
(3)当梯形的高是l0cm时,y=9×10=90,
当梯形的高是l0cm时,y=9×1=9,
梯形的面积由90cm²变化到9cm².
故答案为梯形的高,梯形的面积,y=9x,90,9.
【点拨】此题主要考查了列函数关系式,以及求函数值,关键是掌握梯形的面积公式.
初中数学人教版八年级下册17.1 勾股定理精练: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10261_t7/?tag_id=28" target="_blank">17.1 勾股定理精练</a>,共27页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题 19.4 变量与函数(培优篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版): 这是一份专题 19.4 变量与函数(培优篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版),共43页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题 19.2 变量与函数(基础篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版): 这是一份专题 19.2 变量与函数(基础篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版),共25页。试卷主要包含了函数概念,函数解析式,函数自变量的取值范围,求函数自变量的值或函数值,表格法表示函数关系,解析法表示函数关系,图象法表示函数关系等内容,欢迎下载使用。












