

专题 19.4 变量与函数(培优篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版)
展开专题 19.4 变量与函数(培优篇)(专项练习)
一、单选题
1.函数中,自变量x的取值范围( )
A.x>﹣4 B.x>1 C.x≥﹣4 D.x≥1
2.设函数,以下结论正确的是( ).
A. B.若,则
C. D.
3.下列语句中,与是一次函数关系的有( )个.
(1)汽车以80千米/时的速度匀速行驶,行驶路程(千米)与行驶时间(时)之间的关系;
(2)圆的面积(厘米)与它的半径(厘米)之间的关系;
(3)一棵树现在高50厘米,每个月平均长高2厘米,月后这棵树的高度是厘米,与的关系;
(4)猪肉的单价是60元/千克,当购买千克猪肉时,花费元,与的关系.
A.1 B.2 C.3 D.4
4.表示关于的函数,若,在的取值范围内,且,均有对应的函数值,则称函数在取值范围内是非减函数.已知函数当时为非减函数,且满足以下三个条件:①,② ,③;则的值为( )
A. B. C. D.1
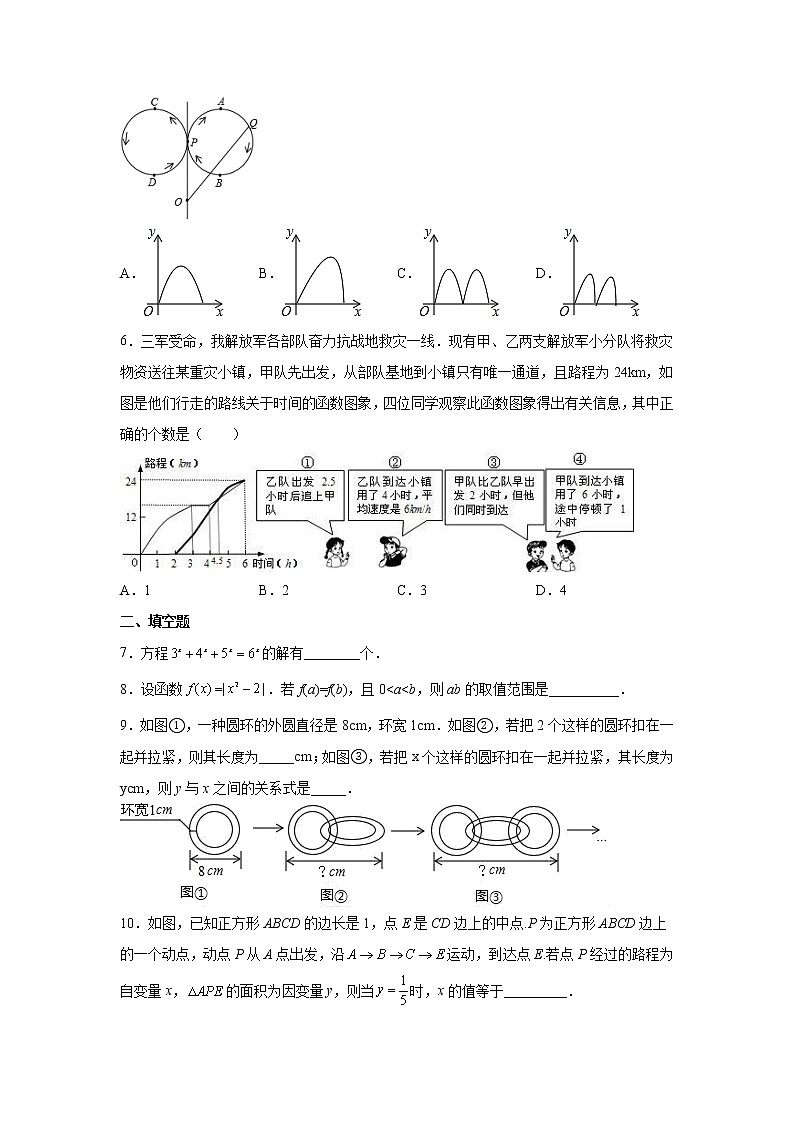
5.如图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处点O与点P不重合利用仪器测量了的大小设蜜蜂飞行时间为的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C. D.
6.三军受命,我解放军各部队奋力抗战地救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到小镇只有唯一通道,且路程为24km,如图是他们行走的路线关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
7.方程的解有________个.
8.设函数.若f(a)=f(b),且0
10.如图,已知正方形ABCD的边长是1,点E是CD边上的中点.P为正方形ABCD边上的一个动点,动点P从A点出发,沿运动,到达点E.若点P经过的路程为自变量x,的面积为因变量y,则当时,x的值等于_________.
三、解答题
11.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若,都有,则称f(x)是增函数;
(2)若,都有,则称f(x)是减函数.
例题:证明函数f(x)=是减函数.
证明:设,
∵,
∴.
∴.即.
∴.
∴函数是减函数.
根据以上材料,解答下面的问题:
已知函数f(x)=(x<0),例如f(-1)==-3,f(-2)==-
(1)计算:f(-3)= ;
(2)猜想:函数f(x)=(x<0)是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
12.如图,将一块三角板放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,一直角边始终经过点B,另一直角边与射线DC相交于点Q.设AP=x.
(1)当点Q在边CD上时,线段PQ与线段PB有怎样的数量关系?试证明你观察得到的结论;
(2)是否存在点P(P不与A重合),使△PCQ为等腰三角形?若存在,请求出相应的x值;若不存在,请说明理由;
(3)设以点B,C,P,Q为顶点的多边形的面积为y,试确定y与x之间的函数关系式.
13.如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF.连接CE、CF.
(1)求证:CE=CF;
(2)如果∠BAD=60°,CD=.
①当AF=时,设,求与的函数关系式;(不需要写定义域)
②当AF=2时,求△CEF的边CE上的高.
14.如图,在△ABC中,AC=BC=4,∠ACB=90°,动点P从点A出发,沿AB以每秒个单位长度的速度向点B运动,点Q从点A出发,沿折线AC﹣CB向点B以每秒2个单位长度的速度运动,过点P作AC的平行线与过点Q作AB的平行线交于点D,当有一个点到达终点时,另一个点也停止运动,设△PQD与△ABC重叠部分图形的面积为S,运动的时间为t(秒)
(1)点P到AC的距离为 (用含t的代数式表示)
(2)当点D落在BC上时,求t的值
(3)当△PQD与△ABC重叠部分图形是三角形时,求S与t的函数关系式(S>0)
15.如图,已知,直线,点P在线段上,点D为射线上一动点,连接,射线交直线于点E.已知,.
(1)如图1,当点D在线段上时,求证:;
(2)当时,请在图2中画出相应的图形,并求线段的长;
(3)如果的平分线交射线于点G,设,,求y关于x的函数关系式,并写出自变量x的取值范围.
16.如图,正方形边长cm,点在边上,且cm,点从点出发,以5cm/s的速度在、之间往返匀速运动,同时,点从点出发,以2cm/s的速度沿路径匀速运动,当点运动到点时,两点都停止运动,设运动时间为(单位:s).在运动过程中的面积(单位:)随运动时间的变化而变化.
(1)当点运动到点时,求值及此时的面积.
(2)在整个运动过程中,求与的关系式.
7.如图①,在矩形ABCD中,AB=8,AD=4.点P从点A出发,沿A→D→C→D运动,速度为每秒2个单位长度;点Q从点 A出发向点B运动,速度为每秒1个单位长度. P、Q两点同时出发,点Q运动到点B时,两点同时停止运动,设点Q的运动时间为t(秒).连结PQ、AC、CP、CQ.
(1)点P到点C时,t= ; 当点Q到终点时,点P的运动路程为 ;
(2)用含t的代数式表示PD的长;
(3)设△CPQ的面积为,求与t之间的函数关系式;
(4)如图②,当点P在线段DC上运动时,将△APQ沿PQ折叠,点A落在平面内的点A′ 处,PQ与AC交于点E.当与△ACD 的边DC、AC平行时,直接写出t的值.
18.如图(1),Rt△AOB中,∠A=90°,,OB=2,∠AOB的平分线OC交AB于C,过作与垂直的直线.动点从点出发沿折线以每秒1个单位长度的速度向终点运动,运动时间为t秒,同时动点Q从点C出发沿折线以相同的速度运动,当点到达点时,同时停止运动.
(1)OC= ,BC= ;
(2)设△CPQ的面积为S,求S与t的函数关系式;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当为何值时,△OPM为等腰三角形?求出所有满足条件的t值.
19.数学家欧拉最先把关于的多项式用记号来表示,例如,并把常数时多项式的值用来表示,例如时多项式的值记为.
(1)若规定,
①的值是_________;
②若,的值是_________;
(2)若规定,.
①有没有能使成立的的值,若有,求出此时的值,若没有,请说明理由,
②直接写出的最小值和此时满足的条件.
20.如图,已知ABC中,,,AB=6,点P是射线CB上一点(不与点B重合),EF为PB的垂直平分线,交PB于点F,交射线AB于点E,联结PE、AP.
(1)求∠B的度数;
(2)当点P在线段CB上时,设BE=x,AP=y,求y关于x的函数解析式,并写出函数的定义域;
(3)当APB为等腰三角形时,请直接写出AE的值.
21.如图,点A(a,0)、B(0,b),且a、b满足(a﹣2)2+|2b﹣4|=0.
(1)如图1,求△AOB的面积;
(2)如图2,若P为AB的中点,点M,N分别是OA,OB边上的动点,点M从顶点A出发向O运动,点N从顶点O向点B运动,且他们的速度都是1个单位长度/秒,在点M和点N的运动过程中,探究线段PM和PN之间的位置和数量关系;
(3)若P为线段AB上异于A、B的任意一点,过点B作BF垂直于直线OP于点F,并延长交x轴于点D,E为x轴上一点,且∠PEA=∠BDO(BD与PE不平行).
①如图3,F在线段OP上,求证:OD=AE;
②设OD=x,DE=y,请直接写出y与x的数量关系式.
参考答案
1.B
【解析】
【详解】
根据二次根式有意义的条件和分式有意义的条件,即x+4≥0,x-1>0,即x>1.
故选B.
2.D
【解析】
【分析】
中x即自变量,把自变量的值代入解析式计算,然后进行判断即可.
【详解】
f(a)+f(−a)=a(a−1)−a(−a−1)=2a2,A不正确;
f(a)=a,即a(a−1)=a,即a(a−2)=0,则a=0或2,B不正确;
f(a)f(-a)=a(a−1)×[−a(−a−1)]= a4- a2,C不正确;
f(a)= a(a−1),f(1−a)=(1-a)(1-a-1)=(1-a)(-a)= a(a−1),D正确,
故选D.
【点拨】本题考查求函数值,在本题中代入自变量时需注意当自变量为-a或1-a时需将-a或1-a看成一个整体,去替换关系式中的x.还需注意化简时的符号问题.
3.C
【解析】
【分析】
根据语句分别列关系式即可得到答案.
【详解】
(1)可得y=80x,是一次函数;
(2),不是一次函数;
(3)y=50+2x,是一次函数;
(4)y=60x,是一次函数,
故选:C.
【点拨】此题考查列函数关系式,一次函数的定义,正确各事件中各量之间的关系列出函数关系式是解题的关键.
4.C
【解析】
【分析】
令x=1,求出f()的值,当x=时,求出f(),得到f()=f(),得出当≤x≤时,f(x)=,再令x=得到f()=,将x=代入②得到f()即可解答.
【详解】
解:令x=1,则f()=f(1),
∵f(1−0)=1−f(0)=1,
∴f()=×1=,
当x=时,f(1−)=1−f(),
所以,当f()=1−f()=1−=,
所以,f()=f()=,
∵函数当时为非减函数,
∴当≤x≤时,f(x)=,
∴令x=,f()=,
则f()=f(×)=f()=×=,
∴f()+f()=+=.
故选:C.
【点拨】本题考查了函数值求解,难度较大,关键在于求出当≤x≤时,f(x)=.
5.D
【解析】
【详解】
如下图,由题意可知,∠POQ随点Q的运动的而变化经历了以下过程:(1)当点Q从点P出发,经过点A到点M的过程中,∠POQ的度数从0变到最大,这一过程用时较长;(2)当点Q从点M开始,经过点B回到点P的过程中,∠POQ的度数从最大变回0,这一过程用时较短;(3)当点Q从P出发经过点C到点N的过程中,∠POQ的度数再次从0变到最大,这一过程用时较长;(4)当点Q从点N开始,经过点D回到点P的过程中,∠POQ的度数再次从最大变回0,这一过程用时较短.
∴能表示y与x函数关系的图象是D选项中的图.
故选D.
点睛:本题的解题要点有两点:(1)通过分析题意,找到∠POQ最大时点Q的位置(即图中的点M、N处);(2)分析出∠POQ的度数由0变到最大,再由最大变回0所需时间的差异.
6.D
【解析】
【详解】
试题分析:从图形上来看甲、乙两支解放军小分队行走的路线关于时间的函数图象第一次相遇在图中的标志是它们有交点,观察图象得t=4.5,而乙是从2这点开始出发的,所以乙追上甲时所花时间=4.5-2=2.5,所以第一个同学是正确的;观察图象乙队到达小镇的时间=6-2=4小时,所以第二个同学正确;从图象上来看,两队出发的时间不同,甲从原点开始出发,乙从(2,0)这点才出发,所以甲队比乙队早出发两个小时;从图象上来看,甲队到达目的地总共用了6个小时,在甲的图象中3-4小时,甲的路程没变,说明在3-4小时这一个小时内甲队停顿了
考点:函数图象
点评:本题考查函数图象,是一个路程与时间的问题,解本题的关键是学生会看图,从图中得出有用的信息
7.1
【解析】
【详解】
由题意=1,而、、均随x的增大而减小,而且值都取到0到1之间.于是原方程有且仅有一个解.故答案为1.
8.
【解析】
【分析】
根据函数解析式,根据绝对值的意义,写出分段函数的自变量的取值范围,根据,列出等式,根据完全平方公式的变形即可求得的取值范围
【详解】
,
当时,,
当时,,
,
,且,
,
,
,
即,
,,
,
即,
,
,
,
故答案为:
【点拨】本题考查了函数的解析式,完全平方公式,平方的非负性质,根据完全平方公式的变形以及平方的非负性求得范围是解题的关键.
9. 14 y=6x+2.
【解析】
【分析】
根据题意和图形可以分别求得把2个这样的圆环扣在一起并拉紧的长度和把x个这样的圆环扣在一起并拉紧的长度.
【详解】
解:由题意可得,把2个这样的圆环扣在一起并拉紧,则其长度为:8+(8-1-1)=14cm,把x个这样的圆环扣在一起并拉紧,其长度为y与x之间的关系式是:y=8+(8-1-1)(x-1)=6x+2,故答案为14,y=6x+2.
【点拨】本题考查函数关系式,解答本题的关键是明确题意,利用数形结合的思想解答.
10.或或
【解析】
【分析】
经过分析,点P只有在AB边,或者BC边上,或DC边上时,才有y=.根据P点的位置,由三角形面积公式表达出分段函数,在分段函数中,已知y的值,求x.
【详解】
经过分析,点P只有在AB边,或者BC边上,或DC边上时,才有y=,
当点P在AB边上时,y=•x•1=,解得x=,
当点P在BC边上时,如图所示,y=•(1+)•1-•(x-1)•1-••(2-x)=,
解得x=;
当点P在DC边上时,y=×(1+1+-x)×1=,
解得:x=,
综上所述,当y=时,x的值等于或或,
故答案为或或
【点拨】此题考查了由动点的运动变化来列函数关系式,应注意自变量的变化范围分段来列.
11.(1);(2)减;(3)详见解析
【解析】
【分析】
(1)根据题目中函数,将代入f(x)=(x<0),即可求解f(-3)的值;
(2)取,代入函数f(x)=(x<0),求得f(-2)的值,结合(1)比较f(-3)和f(-2)的大小,再根据材料信息进行判断即可;
(3)根据题目中例子的证明方法,结合(1)和(2)可证明猜想成立.
【详解】
解:(1)计算:f(-3)==,
故答案为:;
(2)由(1)知,f(-3)=,
当时,f(-2)=,
∵,,
∴猜想:函数f(x)=(x<0)是减函数
故答案为:减;
(3)证明:设,
=,
∵,
∴,,,
∴,
即,
∴,
∴函数f(x)=(x<0)是减函数,猜想得证.
【点拨】本题考查函数的概念,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的性质解答.
12.(1)PQ=PB,证明见解析;(2)存在,x=1;(3)y═x2﹣x+1(0≤x≤);y=x(<x≤).
【解析】
【分析】
(1)如图1中,PQ=PB,过P点作MN∥BC分别交AB、DC于点M、N,可以证明Rt△MBP≌Rt△NPQ;
(2)△PCQ可能成为等腰三角形.①当点P与点A重合时,点Q与点D重合,PQ=QC,(此种情形不符合题意);
②如图2中,当点Q在DC的延长线上,且CP=CQ时,就可以用x表示出面积.
(3)分两种情形分别求解:①如图1中,当点Q在线段CD上时,S四边形PBCQ=S△PBC+S△PCQ分别表示出△PBC于△PCQ的面积就可以.②当点Q在DC的延长线上时,同法可求.
【详解】
解:(1)结论:PQ=PB,
理由:如图1中,过P点作MN∥BC分别交AB、DC于点M、N,
在正方形ABCD中,AC为对角线,
∴AM=PM,
又∵AB=MN,
∴MB=PN,
∵∠BPQ=90°,
∴∠BPM+∠NPQ=90°;
又∵∠MBP+∠BPM=90°,
∴∠MBP=∠NPQ,
在Rt△MBP≌Rt△NPQ中,
∵,
∴Rt△MBP≌Rt△NPQ,
∴PB=PQ.
(2)△PCQ可能成为等腰三角形.
①当点P与点A重合时,点Q与点D重合,
PQ=QC,此时,x=0.(此种情形不符合题意).
②如图2中,当点Q在DC的延长线上,且CP=CQ时,
有:QN=AM=PM=x,CP=﹣x,CN=CP=1﹣x,CQ=QN﹣CN=x﹣(1﹣x)=x﹣1,
∴当﹣x=x﹣1时,x=1.
(3)①如图1中,当点Q在线段CD上时.
∵S四边形PBCQ=S△PBC+S△PCQ,
∵AP=x,
∴AM=x,
∴CQ=CD﹣2NQ=1﹣x,
又∵S△PBC=BC•BM=•1•(1﹣x)=﹣x,
S△PCQ=CQ•PN=(1﹣x)•(1﹣x),
=x2﹣x+,
∴S四边形PBCQ=x2﹣x+1(0≤x≤).
即y═x2﹣x+1(0≤x≤).
②当点Q在DC的延长线上时,
S四边形PCQB=S△PBC+S△BCQ=×1×(1﹣x)+×1×(x﹣1)=x(<x≤).
即y=x(<x≤).
【点拨】本题主要考查正方形的性质、等腰三角形的存在性问题及函数,关键是根据正方形的性质得到线段关系,然后由等腰三角形的性质进行分类讨论,本题对于分类讨论思想运用的还是很好的.
13.(1)见解析;(2)①;②.
【解析】
【分析】
(1)先证明△ACD≌△ACB,再证明△CAF≌△CAE即可;
(2)①分别求出AO,EO和CO的长,再根据三角形面积公式求解即可;
②先求出CE的长,再求出△CEF的面积即可.
【详解】
(1)证明:连接AC,
∵∠ADC=∠ABC=90°,
在Rt△ACD和RT△ACB中,
,
∴△ACD≌△ACB(HL),
∴∠CAF=∠CAE,
在△CAF和△CAE中,
,
∴△CAF≌△CAE(SAS),
∴CE=CF;
(2)①设AC与EF交于点O,
∵AE=AF,∠BAD=60°
∴△AFE是等边三角形,
由(1)知∠CAF=∠CAE=30°,
∴AC⊥FE,
∵AF=x,
∴EF=x,FO=,AO=,
∵∠ADC=90°,∠CAF =30°,CD=,
∴AC=,
∴CO=-,
∵,
∴;
②作FH⊥EC于H,
∵△ACD≌△ACB,∠DAB=60°,
∴AD=AB,∠CAD=∠CAB=30°,
在Rt△ACD中,∠D=90°,CD=2,
∴AC=2CD=4,AD=,
∴DF=AD-AF=4,CE=CF==,
由(2)①可得:当AF=2时,S△EFC=,
又∵S△EFC=CE•FH,
∴3=×2FH,
∴FH=,
∴△CEF的边CE上的高为.
【点拨】本题考查全等三角形的判定和性质、勾股定理等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,求高想到求面积,属于中考常考题型.
14.(1)t;(2)t的值是或;(3)S=
【解析】
【分析】
(1)根据速度和时间可得AP=t,根据等腰直角三角形的性质可得点P到AC的距离PE的长;
(2)有两种情况:①当Q在边BC上时,D落在BC上,D与Q不重合时;②当Q在边BC上时,D与点Q重合时;
(3)当△PQD与△ABC重叠部分图形是三角形时,有三种情况:①当0<t≤时, Q在AC上,当2≤t<时, Q在BC上,③当<t<4时,Q在BC上.
【详解】
解:(1)如图1,过P作PE⊥AC于E,
由题意得:AP=t,
∵AC=BC=4,∠ACB=90°,
∴△ACB是等腰直角三角形,
∴∠A=45°,
∴△APE是等腰直角三角形,
∵AE2+PE2=AP2,
∴PE==t,
故答案为:t;
(2)当D落在BC上,D与Q不重合时,如图2,CD=CQ,
∴4﹣2t=t,t=,
当D落在BC上,D与Q重合时,如图3,CD=CQ,
∴2t﹣4=t,t=,
综上所述,t的值是或;
(3)①当0<t≤时,如图4,Q在AC上,过点P作PE⊥AC于点E,
∵PD//AQ,QD//AP,
∴四边形APDQ是平行四边形,
∴PD=AQ=2t,
∴S=PD•PE=t=;
②当2≤t<时,如图5,Q在BC上,CQ=2t﹣4,PF=BF=BC-CF=4﹣t,
FQ=CF﹣CQ=t-(2t﹣4),
∴S=PF•FQ==﹣4t+8;
③当<t<4时,Q在BC上,如图6,延长PD交BC于F点,
CQ=2t﹣AC=2t﹣4,DF=FQ=CQ﹣CF=2t﹣4﹣t=t﹣4,
PD=PF﹣DF=4﹣t﹣(t﹣4)=8﹣2t,
∴S=PD•FQ=•(8﹣2t)(t﹣4)=﹣+10t﹣16,
综上所述,S与t的函数关系式(S>0):S=.
【点拨】此题考查了三角形的综合,用到的知识点是等腰直角三角形的性质、平行四边形的判定和性质、勾股定理等知识,并与方程相结合,关键是根据题意画出图形,分情况进行讨论,避免出现漏解.
15.(1)见解析;(2)图见解析,2;(3)
【解析】
【分析】
(1)先判断出,进而判断出,再判断出,得到即可;
(2)依题意画出图形,由(1)得到,再判断出,求出,进而求出AE;
(3)先表示出,再判断出,得到,在中,,即,即可.
【详解】
(1)证明:如图1,
作于点H,作于点F,
,
.
,
.
,即,
.
,
.
,
,
,
,
,
;
(2)如图2,
作于点H,作于点F,
同(1)得,
,
,
,
.
,
.
,
.
,
,
,
.
∵在四边形AHPF中,,
∴四边形AHPF是矩形,
,
;
(3)如图3,
作于点H,作于点F,
由(2)得,
,
,
,
,
.
∵PG平分,
.
,
,
,
在中,,
即,
.
【点拨】本题主要考查全等三角形的性质和判定,矩形的判定及性质,同角的余角相等,勾股定理,证明出是关键.
16.(1)t=2,此时的面积=40;(2)见解析
【解析】
【分析】
(1)先根据点的运动速度得出时间,再得出AM的长,再根据三角形的面积公式即可得出答案;
(2)分①当0<t≤2时,②当2<t≤3时,③当3<t≤4时,④当4<t≤6时,⑤当6<t≤8时,五种情况进行讨论即可.
【详解】
解:(1)∵当点运动到点时,cm,点的速度为5cm/s,
∴,
∵点的速度为2cm/s,
∴EM=2×2=4cm,
∴AM=AE+EM=4+4=8,
∴的面积=.
(2)∵当点运动到点时,两点都停止运动,
∴,
①当0<t≤2时,AN=5t,AM=4+2t,
的面积=;
②当2<t≤3时,AN=20-5t,AM=4+2t,
的面积=;
③当3<t≤4时,AN=20-5t,的高为10cm,
的面积=;
④当4<t≤6时,AN=5t-20,的高为10cm,
的面积=;
⑤当6<t≤8时,AN=40-5t,的高为10cm,
的面积=;
【点拨】本题主要考查了正方形的性质和三角形的面积计算,分类讨论的数学思想,确定点M、N所在的位置,是解决本题的关键.
17.(1)6,16(2)当<t≤2时,PD = 4-2t,当2<t≤6时PD = 2t -4,当6<t≤8时,PD = 20 -2t;(3)当<t≤2时,,当2<t≤6时,,当6<t≤8时,;(4)
【解析】
【分析】
(1)计算AC的长,除以速度即可;计算点Q的运算时间AB÷速度,得到的时间乘以点P的速度即可;
(2)根据t的运动特点,分<t≤2,2<t≤6,6<t≤8三种情形计算;
(3)根据(2)的情形,对应计算三角形的面积即可;
(4)在2<t≤6,6<t≤8两种情形下,分别计算∥DC和∥AC计算.
【详解】
解:(1)当点到点时 , t==6,
∵点Q的运动时间为:8÷1=8,
故答案为:6,16;
∴点P 的运动路程为2×8=16
(2)当<t≤2时,
∵PA=2t,PA+PD=AD=4,
∴PD = 4-2t;
当2<t≤6时,
∵PA=2t,AD+PD=PA,AD=4,
∴PD = 2t -4;
当6<t≤8时,
∵2t=AD+CD+PC,PC+PD=CD,AD=4,
∴PD =8-(2t-12)= 20 -2t;
(3)当<t≤2时,
=
;
当2<t≤6时,
;
当6<t≤8时,
;
(4)当2<t≤6,且∥AC时,如图1,
根据折叠的意义,得∠AQP=∠QP,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠AQP=∠CPE,
∵∥AC,
∴∠QP =∠CEP,
∵∠AEQ=∠CEP,
∴∠AQP=∠CPE=∠QP =∠CEP=∠AEQ,
∴AE=AQ,CP=CE,
∵四边形ABCD是矩形,AB=8,AD=4
∴BC=4,∠ABC=90°,
AC==,
设点Q运动时间为t,则PA=2t,AQ=t,
∴CP=12-PA=12-2t,
∵AE+EC=AC,
∴AQ+PC=AC,
∴12-2t+t=,
∴t=12-;
当2<t≤6,且∥DC时,如图2,
根据折叠的意义,得∠AQP=∠QP=90°,
∵四边形ABCD是矩形,
∴∠DAQ=90°,
∴AD∥PQ,
∴四边形AQPD是矩形,
∴PD=AQ,
设点Q运动时间为t,则PA=2t,AQ=t,
∴PD=2t-4,
∴2t-4=t,
∴t=4;
当6<t≤8,且∥AC时,如图3,
根据前面的证明,得到AC=,CP=CE,AQ=AE,
设点Q运动时间为t,则AQ=t, CP=2t-12,
∵AE+EC=AC,
∴AQ+PC=AC,
∴2t-12+t=,
∴t=4+;
当6<t≤8,且∥DC时,如图4,
根据前面的证明,得到AQ=PD,
设点Q运动时间为t,则AQ=t, DP=20-2t,
∴20-2t=t,
∴t=;
综上所得,t的值为.
【点拨】本题考查了矩形的性质,折叠的性质,等腰三角形的判定与性质,平行线的性质,勾股定理,函数的表达式,分类思想,灵活运用分类思想,适当分割图形表示面积是解题的关键.
18.(1)2,2;(2);(3)或
【解析】
【分析】
(1)先求出,根据含30度角的直角三角形的性质求出OA,求出AB,在△AOC中,根据勾股定理得出关于OC的方程,求出OC即可;
(2)有四种情况:①当P在BC上,Q在OC上时,t<2,过P作PH上OC于H,求出PH,根据三角形的面积公式求出即可;②当t=2时,P在C点,Q在O点,此时,△CPQ不存在;③当P在OC上,Q在ON上时,过P作PG上ON于G,过C作CZ上ON于Z,求出CZ和PG的值,求出△OCQ和△OPQ的面积,相减即可;④t=4时,过作于,于, P在O点,Q在ON上,求出BM根据三角形的面积公式求出即可;
(3)有三种情况:①OM=PM时,求出OP=2OQ,代入求出即可;②PM=OP时,此时不存在等腰三角形;③OM=OP时,过P作PG上ON于G,求出OG和QG的值,代入OG+QG=t-2,即可求出答案.
【详解】
(1),
,
,
,
平分,
,
,
在中,,
,
,
故答案为:2,2;
(2)①当P在BC上,Q在OC上时,,
则,
过作于,
,
,
,
即,
②当时,在C点,Q在O点,此时,△CPQ不存在;
,
③当P在OC上,Q在ON上时,过P作PG上ON于G,过C作CZ上ON于Z,
,
,,
,
,
,
即,
④当时,过作于,于, P在O点,Q在ON上,
,由(1)知,
,
,
,
,
,
综上所述,与的函数关系式是:;
(3)如图,
,
,
,
,
平分,
,
,
①时,,
,
,
,
解得:,
②当时,
此时,
,
,
此时不存在;
③当时,
过作于,
,
,
,
,
,
,
,
,
解得:.
综上所述,当为或者时,是等腰三角形.
【点拨】本题考查了等腰三角形的性质,三角形的面积,函数自变量的取值范围,勾股定理,含30度角的直角三角形性质等知识点的运用,运用了方程思想和分类讨论思想是解题的关键.
19.(1)①-5;②5,
(2)①有,x=,见解析;②的最小值是5,-3≤x≤2
【解析】
【分析】
(1)①当x=-1时,计算;
②计算,求得x即可;
(2)①或,解方程即可;
②表示动点x到2和-3的距离和,按照x>2,x<-3,-3≤x≤2分别计算比较结果即可.
(1)
(1)①∵,
∴当x=-1时, =-5,
∴的值是-5,
故答案为:-5;
②∵,
∴=7,
∴x=5,
故答案为:5;
(2)
①有,x=,理由如下:
∵,,且,
∴,无解;
或,
解得x=,
故当x=时,;
②设动点P表示的数为x,点A表示的数是-3,点B表示的数2,
则表示数轴上动点P到点A和点B的距离和即PA+PB,
当x>2时,如图所示,
PA+PB>AB=2-(-3)=5;
当x<-3时,如图所示,
PA+PB>AB=2-(-3)=5;
当-3≤x≤2时,如图所示,
,
PA+PB=x+3+2-x=5=AB=2-(-3)=5;
故当-3≤x≤2时,有最小值,且为5.
【点拨】本题考查了求函数值,自变量的值,解方程,绝对值的化简,数轴上的动点问题,熟练掌握绝对值的化简,数轴上的动点问题是解题的关键.
20.(1)
(2)当点P在线段BC上时,;当点P在CB延长线上时,
(3)4或或
【解析】
【分析】
(1)根据勾股定理的逆定理证明出△ABC是直角三角形,且∠BAC=,取BC的中点M,连接AM,则=CM,证得△ACM是等边三角形,求得∠B=;
(2)当点P在线段BC上时,过点A作AD⊥BC于D,根据直角三角形的性质得到,,由勾股定理得,求出,得到,由勾股定理求出CD,BF,得到DP,由,推出,根据y>0,得到函数关系式;当点P在CB延长线上时,过点P作PH⊥AB交延长线于H,求出,勾股定理求得PH,根据,求出函数解析式;
(3)当AP=BP时,根据等腰三角形等边对等角的性质及线段垂直平分线的性质证得∠APE=,得到AE=2PE=2BE,由此求出AE=4;当BP=AB=6时,根据线段垂直平分线的性质求出PF=BF=3,利用直角三角形30度角的性质求出BE=2EF,利用勾股定理得,求出BE,即可得到AE的值.当点P在CB延长线上且BP=AB=6时,根据线段垂直平分线的性质求出PF=BF=3,利用直角三角形30度角的性质求出BE=2EF,利用勾股定理得,求出BE,即可得到AE的值.
(1)
解:ABC中,,,AB=6,
∵,
∴△ABC是直角三角形,且∠BAC=,
取BC的中点M,连接AM,则=CM,
∵,,
∴,
∴AC=AM=CM,
∴△ACM是等边三角形,
∴,
∴∠B=;
(2)
解:当点P在线段BC上时,
过点A作AD⊥BC于D,
在△ADB中,∠ADB=,∠B=,
∴,
同理,
∴,
在Rt△BEF中,,
∴,
∴,
又∵BP=2BF,
∴,
∴DP =,
∵,
∴,
∴,
∵y>0,
∴;
当点P在CB延长线上时,过点P作PH⊥AB交延长线于H,
∵PE=BE=x,,
∴,
∴,
∴,
∵,
∴,
∴,
∵y>0,
∴;
综上,当点P在线段BC上时,;当点P在CB延长线上时,;
(3)
解:当AP=BP时,则∠PAB=∠B=,如图,
∴∠APB =,
∵EF为PB的垂直平分线,
∴PE=BE,
∴∠BPE=∠B=,
∴∠APE=,
∴AE=2PE=2BE,
∵AE+BE=6,
∴AE=4;
当BP=AB=6时,如图,
∵EF为PB的垂直平分线,
∴PF=BF=3,
∵∠B=,
∴BE=2EF,
∵,
∴,
∴AE=AB-BE=;
当点P在CB延长线上且BP=AB=6时,如图,
∵EF为PB的垂直平分线,
∴PF=BF=3,
∵∠EBF=,
∴BE=2EF,
∵,
∴,
∴AE=AB+BE=;
综上,AE的值为4或或.
【点拨】此题考查了勾股定理及逆定理,直角三角形30度角的性质,线段垂直平分线的性质,等腰三角形的性质,求函数解析式,熟记各知识点并综合应用是解题的关键.
21.(1)
(2),
(3)①见解析;②
【解析】
【分析】
(1)利用非负数的性质可求得:、,再运用三角形面积公式即可求得答案;
(2)如图2,连接,运用等腰直角三角形性质和题意可证得,运用全等三角形性质即可得出答案;
(3)①如图3,过点作交的延长线于点,先证得,再证得,即可得出答案;②如图3,设,,则,利用,即可得出;如图4,过点作交的延长线于点,先证得,再证得,得出,设,,则,由,即可得出.
(1)
解:,
,,
解得:,,
、,
,
如图1,,
;
(2)
解:如图2,连接,
,,为的中点,
,,,
点从顶点出发向运动,点从顶点向点运动,且他们的速度都是1个单位长度秒,
,
在和中,
,
,
,,
,
,
综上所述,,;
(3)
解:①如图3,过点作交的延长线于点,
则,
于点,
,
,
,
,
在和中,
,
,
,,
,
,
,,
,
,
在和中,
,
,
,
;
②如图3,设,,则,
,
,
,
如图4,过点作交的延长线于点,
则,
,,,
,
在和中,
,
,
,
,
,
在和中,
,
,
,
设,,则,
,
,
,
综上所述,与的数量关系式为.
【点拨】本题考查了全等三角形判定和性质,非负数的性质,等腰直角三角形性质等及坐标与图形,解题关键是正确添加辅助线构造全等三角形.
初中数学17.1 勾股定理课时作业: 这是一份初中数学<a href="/sx/tb_c10261_t7/?tag_id=28" target="_blank">17.1 勾股定理课时作业</a>,共50页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题 19.8 函数的图象(培优篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版): 这是一份专题 19.8 函数的图象(培优篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版),共34页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
专题 19.3 变量与函数(巩固篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版): 这是一份专题 19.3 变量与函数(巩固篇)(专项练习)-八年级数学下册基础知识专项讲练(人教版),共23页。试卷主要包含了函数概念,函数解析式,函数自变量的取值范围,求函数自变量的值或函数值,表格法表示函数关系,解析法表示函数关系,图象法表示函数关系等内容,欢迎下载使用。












