山东省淄博市沂源县历山中学2022-2023学年九年级上学期期中数学试卷（五四学制）(含答案)

这是一份山东省淄博市沂源县历山中学2022-2023学年九年级上学期期中数学试卷（五四学制）(含答案)，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年山东省淄博市沂源县历山中学九年级第一学期期中数学试卷（五四学制）
一、选择题：本大题共10个小题，每小题4分，共40分。在每小题所给出的四个选项中，只有一项是符合题目要求的.
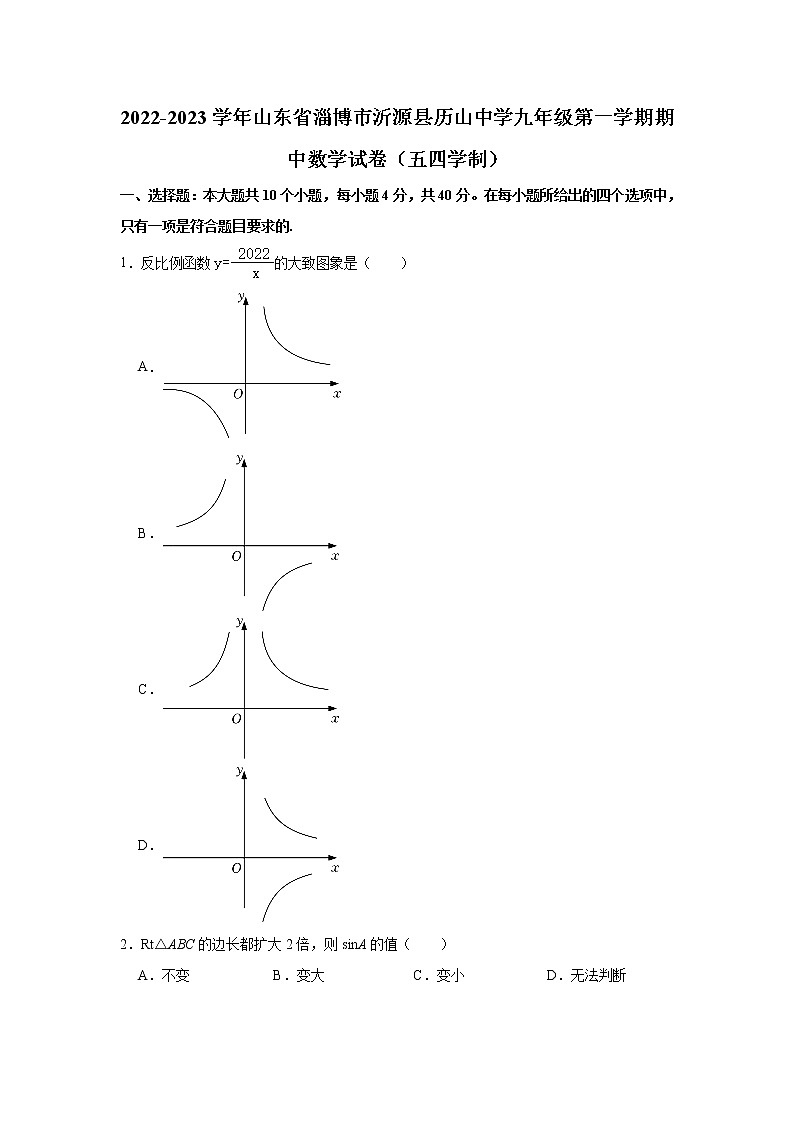
1．反比例函数的大致图象是（　　）
A．
B．
C．
D．
2．Rt△ABC的边长都扩大2倍，则sinA的值（　　）
A．不变 B．变大 C．变小 D．无法判断
3．关于抛物线y＝（x+1）2﹣3的情况描述正确的是（　　）
A．开口向上，对称轴是直线x＝1，顶点坐标是（1，﹣3）
B．开口向下，对称轴是直线x＝﹣1，顶点坐标是（﹣1，3）
C．开口向上，对称轴是直线x＝﹣1，顶点坐标是（﹣1，﹣3）
D．开口向下，对称轴是直线x＝1，顶点坐标是（1，3）
4．在Rt△ACB中，∠C＝90°，AB＝8，sinA＝，则BC的长为（　　）
A．6 B．7.5 C．8 D．12.5
5．二次函数y＝﹣x2+2x﹣4的最大值为（　　）
A．﹣3 B．3 C．5 D．﹣4
6．如图，△ABC的顶点是正方形网格的格点，则sinA的值为（　　）

A． B． C． D．
7．二次函数y＝2x2的图象平移后，得到二次函数y＝2（x+1）2﹣4图象，平移方法是（　　）
A．先向左平移1个单位，再向上平移4个单位
B．先向左平移1个单位，再向下平移4个单位
C．先向右平移1个单位，再向上平移4个单位
D．先向右平移1个单位，再向下平移4个单位
8．如图是反比例函数y1＝和y2＝在x轴上方的图象，x轴的平行线AB分别与这两个函数图象交于A、B两点，点P（﹣5.5，0）在x轴上，则△PAB的面积为（　　）

A．3 B．6 C．8.25 D．16.5
9．已知二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，对称轴为x＝，且经过点（﹣1，0）．下列结论：①3a+b＝0；②若点（，y1），（3，y2）是抛物线上的两点，则y1＜y2；③10b﹣3c＝0；④若y≤c，则0≤x≤3．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
10．当﹣2≤x≤1时，二次函数y＝﹣（x﹣m）2+m2+1有最大值4，则实数m的值为（　　）
A．﹣ B．或﹣ C．2或﹣ D．2或﹣或﹣
二、填空题：本大题共5小题，每小题4分，共20分，只要求填写最后结果。
11．如图，在Rt△ABC中，∠C＝90°，若sinA＝，则cosB＝　 　．

12．若某人沿坡度i＝1：2的斜坡前进10m，则他所在的位置比原来的位置升高 　 　m．
13．观察函数y＝的图象，当y≥﹣2时，x的取值范围是 　 　．
14．抛物线y＝（k﹣1）x2﹣x+1与x轴有交点，则k的取值范围是　 　．
15．如图，已知在平面直角坐标系中，点A在x轴负半轴上，点B在第二象限内，反比例函数y＝的图象经过△OAB的顶点B和边AB的中点C，如果△OAB的面积为6，那么k的值是 　 　．

三、解答题：本大题共8小题，共90分，请写出必要的文字说明、证明过程或演算步骤。
16．反比例函数的图象过点A（2，﹣8）．
（1）求这个函数的表达式；
（2）请判断点B（﹣4，4）是否在这个反比例函数的图象上，并说明理由．
17．为加强生态文明建设，某市环保局对一企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mg/L．环保局要求该企业立即整改，在15天内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度：y（mg/L）与时间x（天）的变化规律如图所示，其中线段AC表示前3天的变化规律，第3天时硫化物的浓度降为4.5mg/L，从第3天起，所排污水中硫化物的浓度y与时间x满足下面表格中的关系：
时间x（天）
3
5
6
9
……
硫化物的浓度y（mg/L）
4.5
2.7
2.25
1.5
……
（1）在整改过程中，当x≥3时，硫化物的浓度y与时间x的函数表达式；
（2）该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L？为什么？

18．如图，湖边A、B两点由两段笔直的观景栈道AC和CB相连．为了计算A、B两点之间的距离，经测量得：∠BAC＝37°，∠ABC＝58°，AC＝80米，求A、B两点之间的距离．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）

19．如图，在Rt△BAD中，延长斜边BD到点C，使DC＝，连接AC，若tanB＝，求tan∠CAD的值．

20．在△ABC中，AB＝8，AC＝5，若BC边上的高等于4，求BC的长．
21．某商店购进了一种消毒用品，进价为每件8元，在销售过程中发现，每天的销售量y（件）与每件售价x（元）之间存在一次函数关系（其中8≤x≤15，且x为整数）．当每件消毒用品售价为9元时，每天的销售量为105件；当每件消毒用品售价为11元时，每天的销售量为95件．
（1）求y与x之间的函数关系式；
（2）设该商店销售这种消毒用品每天获利w（元），当每件消毒用品的售价为多少元时，每天的销售利润最大？最大利润是多少元？
22．如图，抛物线C1：y＝x2﹣bx+4与x轴交于点C（1，0），B，与y轴交于点A，将抛物线C1沿x轴翻折，然后向右平移1个单位，再向上平移1个单位，得到抛物线C2．
（1）直接写出b的值及C2的解析式；
（2）在抛物线C2的第一象限内的图象上有一点P，求△PAB的面积的最大值．

23．抛物线y＝ax2+c与x轴交于A，B两点，顶点为C，点P为抛物线上一点，且位于x轴下方．
（1）如图1，若P（1，﹣3），B（4，0）．
①求该抛物线的解析式；
②若D是抛物线上一点，满足∠DPO＝∠POB，求点D的坐标；
（2）如图2，已知直线PA、PB与y轴分别交于E、F两点，当点P运动时，是否为定值？若是，试求出该定值；若不是，请说明理由．




参考答案
一、选择题：本大题共10个小题，每小题4分，共40分。在每小题所给出的四个选项中，只有一项是符合题目要求的.
1．反比例函数的大致图象是（　　）
A．
B．
C．
D．
【分析】根据反比例函数的性质判断双曲线所在的象限即可．
解：∵反比例函数的图象是双曲线，k＝﹣2022＜0，
∴反比例函数的图象在二、四象限，
故选：B．
【点评】本题考查了反比例函数的图象和性质，熟知反比例函数的性质是解题的关键．
2．Rt△ABC的边长都扩大2倍，则sinA的值（　　）
A．不变 B．变大 C．变小 D．无法判断
【分析】根据题意可得所得的三角形与原三角形相似，从而可得∠A的大小没有发生变化，即可解答．
解：∵Rt△ABC的边长都扩大2倍，
∴所得的三角形与原三角形相似，
∴∠A的大小没有发生变化，
∴sinA的值不变，
故选：A．
【点评】本题考查了解直角三角形，熟练掌握锐角三角函数的定义是解题的关键．
3．关于抛物线y＝（x+1）2﹣3的情况描述正确的是（　　）
A．开口向上，对称轴是直线x＝1，顶点坐标是（1，﹣3）
B．开口向下，对称轴是直线x＝﹣1，顶点坐标是（﹣1，3）
C．开口向上，对称轴是直线x＝﹣1，顶点坐标是（﹣1，﹣3）
D．开口向下，对称轴是直线x＝1，顶点坐标是（1，3）
【分析】根据二次函数的性质判断即可得到结论．
解：关于抛物线y＝（x+1）2﹣3，
开口向上，对称轴是直线x＝﹣1，顶点坐标是（﹣1，﹣3），
故选：C．
【点评】本题考查了二次函数的性质，熟练掌握二次函数的性质是解题的关键．
4．在Rt△ACB中，∠C＝90°，AB＝8，sinA＝，则BC的长为（　　）
A．6 B．7.5 C．8 D．12.5
【分析】根据正弦值的定义解决此题．
解：如图．

∵∠C＝90°，AB＝8，sinA＝，
∴sinA＝．
∴BC＝6．
故选：A．
【点评】本题主要考查正弦值的定义，熟练掌握正弦值的定义是解决本题的关键．
5．二次函数y＝﹣x2+2x﹣4的最大值为（　　）
A．﹣3 B．3 C．5 D．﹣4
【分析】利用二次函数的图象与性质解答即可，当a＜0时，开口向下，顶点是抛物线的最高点，当x＝1时y有最大值是﹣3．
解：∵二次函数y＝﹣x2+2x﹣4＝﹣（x﹣1）2﹣3，
∴抛物线开口向下，顶点是抛物线的最高点，
∴当x＝1时，y有最大值是﹣3；
故选：A．
【点评】本题主要考查二次函数的图象与性质，解题的关键是熟练掌握二次函数的图象与性质．
6．如图，△ABC的顶点是正方形网格的格点，则sinA的值为（　　）

A． B． C． D．
【分析】直接根据题意构造直角三角形，进而利用勾股定理得出DC，AC的长，再利用锐角三角函数关系求出答案．
解：如图所示：连接DC，
由网格可得出∠CDA＝90°，
则DC＝，AC＝，
故sinA＝＝＝．
故选：B．

【点评】此题主要考查了勾股定理以及锐角三角函数关系，正确构造直角三角形是解题关键．
7．二次函数y＝2x2的图象平移后，得到二次函数y＝2（x+1）2﹣4图象，平移方法是（　　）
A．先向左平移1个单位，再向上平移4个单位
B．先向左平移1个单位，再向下平移4个单位
C．先向右平移1个单位，再向上平移4个单位
D．先向右平移1个单位，再向下平移4个单位
【分析】根据平移前后两个抛物线的顶点坐标的变化来判定平移方法．
解：抛物线y＝2x2的顶点坐标是（0，0）．
抛物线y＝2（x+1）2﹣4的顶点坐标是（﹣1，﹣4）．
则由二次函数y＝2x2的图象向左平移1个单位，向下平移4个单位即可得到二次函数y＝2（x+1）2﹣4的图象．
故选：B．
【点评】本题考查了二次函数图象与几何变换．解决本题的关键是根据顶点式得到新抛物线的顶点坐标．
8．如图是反比例函数y1＝和y2＝在x轴上方的图象，x轴的平行线AB分别与这两个函数图象交于A、B两点，点P（﹣5.5，0）在x轴上，则△PAB的面积为（　　）

A．3 B．6 C．8.25 D．16.5
【分析】利用反比例函数的比例系数的几何意义即可得到答案．
解：连接OA、OB，
∵x轴的平行线AB分别与这两个函数图象相交于点A，B．设AB交y轴于C．
∴AB⊥y轴，
∵点A、B在反比例函数y1＝和y2＝在x轴上方的图象上，
∴S△PAB＝S△AOB＝S△COB+S△AOC＝（2+4）＝3，
故选：A．
【点评】本题考查的是反比例函数系数k的几何意义，即在反比例函数y＝的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变．
9．已知二次函数y＝ax2+bx+c（a≠0）的部分图象如图所示，对称轴为x＝，且经过点（﹣1，0）．下列结论：①3a+b＝0；②若点（，y1），（3，y2）是抛物线上的两点，则y1＜y2；③10b﹣3c＝0；④若y≤c，则0≤x≤3．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
【分析】由对称轴为x＝即可判断①；根据点（，y1），（3，y2）到对称轴的距离即可判断②；由抛物线经过点（﹣1，0），得出a﹣b+c＝0，对称轴x＝﹣＝，得出a＝﹣b，代入即可判断③；根据二次函数的性质以及抛物线的对称性即可判断④．
解：∵对称轴x＝﹣＝，
∴b＝﹣3a，
∴3a+b＝0，①正确；
∵抛物线开口向上，点（，y1）到对称轴的距离小于点（3，y2）的距离，
∴y1＜y2，故②正确；
∵经过点（﹣1，0），
∴a﹣b+c＝0，
∵对称轴x＝﹣＝，
∴a＝﹣b，
∴﹣b﹣b+c＝0，
∴3c＝4b，
∴4b﹣3c＝0，故③错误；
∵对称轴x＝，
∴点（0，c）的对称点为（3，c），
∵开口向上，
∴y≤c时，0≤x≤3．故④正确；
故选：C．
【点评】本题考查了二次函数的性质及二次函数图象上点的坐标特征，熟知二次函数的性质是解题的关键．
10．当﹣2≤x≤1时，二次函数y＝﹣（x﹣m）2+m2+1有最大值4，则实数m的值为（　　）
A．﹣ B．或﹣ C．2或﹣ D．2或﹣或﹣
【分析】求出二次函数对称轴为直线x＝m，再分m＜﹣2，﹣2≤m≤1，m＞1三种情况，根据二次函数的增减性列方程求解即可．
解：二次函数对称轴为直线x＝m，
①m＜﹣2时，x＝﹣2取得最大值，﹣（﹣2﹣m）2+m2+1＝4，
解得m＝﹣，不合题意，舍去；
②﹣2≤m≤1时，x＝m取得最大值，m2+1＝4，
解得m＝±，
∵m＝不满足﹣2≤m≤1的范围，
∴m＝﹣；
③m＞1时，x＝1取得最大值，﹣（1﹣m）2+m2+1＝4，
解得m＝2．
综上所述，m＝2或﹣时，二次函数有最大值4．
故选：C．
【点评】本题考查了二次函数的最值，熟悉二次函数的性质及图象是解题的关键．
二、填空题：本大题共5小题，每小题4分，共20分，只要求填写最后结果。
11．如图，在Rt△ABC中，∠C＝90°，若sinA＝，则cosB＝　　．

【分析】根据三角函数的定义即可得到cosB＝sinA＝．
解：在Rt△ABC中，∠C＝90°，
∵sinA＝＝，
∴cosB＝＝．
故答案为：．
【点评】本题考查了三角函数的定义，由定义可推出互余两角的三角函数的关系：若∠A+∠B＝90°，则sinA＝cosB，cosA＝sinB．熟知相关定义是解题关键．
12．若某人沿坡度i＝1：2的斜坡前进10m，则他所在的位置比原来的位置升高 　10　m．
【分析】根据题意作出图形，可得BC：AB＝1：2，设BC＝x，AB＝2x，根据勾股定理可得AC2＝AB2+BC2，代入求出x的值．
解：设BC＝x，AB＝2x，
则AC2＝AB2+BC2，
AC＝＝x＝10，
∴x＝10，
故所在的位置比原来的位置升高了10m．
故答案为：10．

【点评】本题考查了坡度和坡角的知识，解答本题的关键是根据题意构造直角三角形，利用三角函数的知识求解．
13．观察函数y＝的图象，当y≥﹣2时，x的取值范围是 　x＜﹣1或x＞0．　．
【分析】直接画出反比例函数图象，再利用反比例函数的性质结合图象得出x的取值范围．
解：当y＝﹣2时，x＝﹣1，如图所示：
则当y＞﹣2时，x的取值范围是：x＜﹣1或x＞0．
故答案为：x＜﹣1或x＞0．

【点评】本题考查的是反比例函数图象上点的坐标特点，能利用函数图象直接得出不等式的解集是解答此题的关键．
14．抛物线y＝（k﹣1）x2﹣x+1与x轴有交点，则k的取值范围是　k≤且k≠1　．
【分析】直接利用根的判别式得到△＝（﹣1）2﹣4×（k﹣1）×1≥0，再利用二次函数的意义得到k﹣1≠0，然后解两不等式得到k的范围．
解：∵抛物线y＝（k﹣1）x2﹣x+1与x轴有交点，
∴△＝（﹣1）2﹣4×（k﹣1）×1≥0，解得k≤，
又∵k﹣1≠0，
∴k≠1，
∴k的取值范围是k≤且k≠1；
故答案为：k≤且k≠1．
【点评】本题考查了抛物线与x轴的交点：把求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．解题的关键是掌握根的判别式求参数的取值范围．
15．如图，已知在平面直角坐标系中，点A在x轴负半轴上，点B在第二象限内，反比例函数y＝的图象经过△OAB的顶点B和边AB的中点C，如果△OAB的面积为6，那么k的值是 　﹣4　．

【分析】过B作BD⊥OA于D，设B（﹣m，n），根据三角形的面积公式得到OA＝，求得A（﹣，0），根据点C是AB的中点，可得C（﹣，），列方程即可得到结论．
解：过B作BD⊥OA于D，

∵点B在反比例函数y＝的图象上，
∴设B（﹣m，n），点B在第二象限内，
∵△OAB的面积为6，
∴OA＝，
∴A（﹣，0），
∵点C是AB的中点，
∴C（﹣，），
∵点C在反比例函数y＝的图象上，
∴﹣•＝﹣mn，
∴﹣mn＝﹣4，
∴k＝﹣4，
故答案为：﹣4．
【点评】本题考查了反比例函数系数k的几何意义，三角形的面积公式，中点坐标的求法，正确的理解题意是解题的关键．
三、解答题：本大题共8小题，共90分，请写出必要的文字说明、证明过程或演算步骤。
16．反比例函数的图象过点A（2，﹣8）．
（1）求这个函数的表达式；
（2）请判断点B（﹣4，4）是否在这个反比例函数的图象上，并说明理由．
【分析】（1）把点A（2，﹣8）直接代入反比例函数，求得函数解析式即可；
（2）把点B（﹣4，4）代入（1）中的函数解析式，判断即可．
解：（1）∵反比例函数的图象过点A（2，﹣8）．
∴k＝2×（﹣8）＝﹣16，
所以反比例函数的解析式为y＝﹣；

（2）把x＝﹣4代入y＝﹣得，y＝4，
∴点B（﹣4，4）在这个反比例函数的图象上．
【点评】此题考查待定系数法求函数解析式，反比例函数图象上点的坐标体系，将点的坐标代入解析式，利用方程解决问题．
17．为加强生态文明建设，某市环保局对一企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mg/L．环保局要求该企业立即整改，在15天内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度：y（mg/L）与时间x（天）的变化规律如图所示，其中线段AC表示前3天的变化规律，第3天时硫化物的浓度降为4.5mg/L，从第3天起，所排污水中硫化物的浓度y与时间x满足下面表格中的关系：
时间x（天）
3
5
6
9
……
硫化物的浓度y（mg/L）
4.5
2.7
2.25
1.5
……
（1）在整改过程中，当x≥3时，硫化物的浓度y与时间x的函数表达式；
（2）该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L？为什么？

【分析】（1）可推出x•y＝13.5为定值，所以当x≥3时，y是x的反比例函数，进而求得结果；
（2）将x＝15代入反比例函数关系式，从而求得y的值，进而根据反比例函数图象性质，从而得出结论．
解：（1）∵3×4.5＝5×2.7＝13.5，
∴y是x的反比例函数，
∴y＝（x≥3）；
（2）该企业所排污水中硫化物的浓度可以在15天以内不超过最高允许的1.0mg/L，理由如下：
当x＝15时，y＝＝0.9＜1，
∵13.5＞0，
∴y随x的增大而减小，
∴该企业所排污水中硫化物的浓度可以在15天以内不超过最高允许的1.0mg/L．
【点评】本题考查了反比例函数及其图象的性质等知识，解决问题的关键是熟练掌握反比例函数及其图象性质．
18．如图，湖边A、B两点由两段笔直的观景栈道AC和CB相连．为了计算A、B两点之间的距离，经测量得：∠BAC＝37°，∠ABC＝58°，AC＝80米，求A、B两点之间的距离．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）

【分析】通过作高，构造直角三角形，利用直角三角形的边角关系，列方程求解即可．
解：如图，过点C作CD⊥AB，垂足为点D，

在Rt△ACD中，
∵∠DAC＝37°，AC＝80米，
∴sin∠DAC＝，cos∠DAC＝，
∴CD＝AC•sin37°≈80×0.60＝48（米），
AD＝AC•cos37°≈80×0.80＝64（米），
在Rt△BCD中，
∵∠CBD＝58°，CD＝48米，
∴tan∠CBD＝，
∴BD＝≈＝30（米），
∴AB＝AD+BD＝64+30＝94（米）．
答：A、B两点之间的距离约为94米．
【点评】本题考查直角三角形的边角关系，掌握直角三角形的边角关系，即锐角三角函数，是正确解答的前提，通过作辅助线构造直角三角形是常用的方法．
19．如图，在Rt△BAD中，延长斜边BD到点C，使DC＝，连接AC，若tanB＝，求tan∠CAD的值．

【分析】过点C作CE⊥AD，垂足为E，根据tanB＝设AD＝5x，AB＝3x，证△CDE∽△BDA，得出比例式，求出CE＝x，DE＝x，求出AE＝x，解直角三角形得出即可．
解：过点C作CE⊥AD，垂足为E，
∵tanB＝，即＝，
∴设AD＝5x，则AB＝3x，
∵∠CDE＝∠BDA，∠CED＝∠BAD＝90°，
∴△CDE∽△BDA，
∵BD＝2CD，
∴＝＝＝，
∴CE＝x，DE＝x，
∴AE＝x，
∴tan∠CAD＝＝＝．
【点评】本题考查了相似三角形的判定和性质，解直角三角形的应用，能构造直角三角形是解此题的关键．
20．在△ABC中，AB＝8，AC＝5，若BC边上的高等于4，求BC的长．
【分析】作AD⊥BC于D，分点D在线段BC上和BC的延长线上两种情况，根据勾股定理计算即可．
解：作AD⊥BC于D，分两种情况：
①高BD在线段BC上，
如图1所示：
在Rt△ABD中，BD＝＝＝4，
在Rt△ACD中，CD＝＝＝3，
∴BC＝BD+CD＝4+3；
②高AD在CB的延长线上，
如图2所示：
BC＝BD﹣CD＝4﹣3；
综上所述，BC的长为4+3或4﹣3．


【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．
21．某商店购进了一种消毒用品，进价为每件8元，在销售过程中发现，每天的销售量y（件）与每件售价x（元）之间存在一次函数关系（其中8≤x≤15，且x为整数）．当每件消毒用品售价为9元时，每天的销售量为105件；当每件消毒用品售价为11元时，每天的销售量为95件．
（1）求y与x之间的函数关系式；
（2）设该商店销售这种消毒用品每天获利w（元），当每件消毒用品的售价为多少元时，每天的销售利润最大？最大利润是多少元？
【分析】（1）根据给定的数据，利用待定系数法即可求出y与x之间的函数关系式；
（2）利用销售该消毒用品每天的销售利润＝每件的销售利润×每天的销售量，即可得出w关于x的函数关系式，再利用二次函数的性质即可解决最值问题．
解：（1）设每天的销售量y（件）与每件售价x（元）函数关系式为：y＝kx+b，
由题意可知：，
解得：，
∴y与x之间的函数关系式为：y＝﹣5x+150；
（2）w＝y（x﹣8）
＝（﹣5x+150）（x﹣8）
＝﹣5x2+190x﹣1200
＝﹣5（x﹣19）2+605，
∵8≤x≤15，且x为整数，
∴当x＜19时，w随x的增大而增大，
∴当x＝15时，w有最大值，最大值为﹣5×（15﹣19）2+605＝525．
答：每件消毒用品的售价为15元时，每天的销售利润最大，最大利润是525元．
【点评】本题考查了待定系数法求一次函数解析式以及二次函数的应用，解题的关键是找准题目的等量关系列出函数关系式．
22．如图，抛物线C1：y＝x2﹣bx+4与x轴交于点C（1，0），B，与y轴交于点A，将抛物线C1沿x轴翻折，然后向右平移1个单位，再向上平移1个单位，得到抛物线C2．
（1）直接写出b的值及C2的解析式；
（2）在抛物线C2的第一象限内的图象上有一点P，求△PAB的面积的最大值．

【分析】（1）首先利用待定系数法确定抛物线C1的解析式；然后根据二次函数几何图象的变换规律求得C2的解析式；
（2）设P（x，y），由图形知，S△PAB＝S梯形APDC﹣S△OAB﹣S△BPD，由此得到二次函数关系式，根据二次函数最值的求法解答．
解：（1）把点C（1，0）代入y＝x2﹣bx+4，得12﹣b+4＝0，则b＝5．
∴抛物线C1：y＝x2﹣5x+4．
将抛物线C1沿x轴翻折后得到﹣y＝x2﹣5x+4，即新抛物线解析式为y＝﹣x2+5x﹣4．
∵y＝﹣x2+5x﹣4＝﹣（x﹣）2+，
∴将其向右平移1个单位，再向上平移1个单位，得到抛物线C2：y＝﹣（x﹣）2+，
综上所述，b的值是5，抛物线C2：y＝﹣（x﹣）2+或y＝﹣x2+7x﹣9．

（2）设P（x，﹣x2+7x﹣9），
如图，过点P作PD⊥x轴于D，
∵抛物线C1：y＝x2﹣5x+4，
∴A（0，4）．
∵抛物线C1：y＝x2﹣5x+4＝（x﹣4）（x﹣1），
∴C（1，0），B（4，0）．
∴PD＝﹣x2+7x﹣9，OD＝x，OB＝OA＝4，BD＝x﹣4，
∴S△PAB＝S梯形APDO﹣S△OAB﹣S△BPD
＝×（PD+OA）•OD﹣OA•OB﹣BD•PD
＝×（﹣x2+7x﹣9+4）x﹣×4×4﹣（x﹣4）•（﹣x2+7x﹣9）
＝﹣2（x﹣4）2+6．
即：S△PAB＝﹣2（x﹣4）2+6．
∴当x＝4时，S△PAB最大值＝6．
∴△PAB的面积的最大值是6．

【点评】本题主要考查了二次函数综合题，需要综合运用待定系数法确定函数关系式，二次函数图象与几何变换，坐标与图形性质，二次函数最值的求法以及三角形面积公式等知识点，要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．
23．抛物线y＝ax2+c与x轴交于A，B两点，顶点为C，点P为抛物线上一点，且位于x轴下方．
（1）如图1，若P（1，﹣3），B（4，0）．
①求该抛物线的解析式；
②若D是抛物线上一点，满足∠DPO＝∠POB，求点D的坐标；
（2）如图2，已知直线PA、PB与y轴分别交于E、F两点，当点P运动时，是否为定值？若是，试求出该定值；若不是，请说明理由．


【分析】（1）①根据待定系数法求函数解析式，可得答案；
②根据平行线的判定，可得PD∥OB，根据函数值相等两点关于对称轴对称，可得D点坐标；
（2）根据待定系数法，可得E、F点的坐标，根据分式的性质，可得答案．
解：（1）①将P（1，﹣3），B（4，0）代入y＝ax2+c，得：
，解得，
抛物线的解析式为y＝x2﹣①；

②如图1，

当点D在OP左侧时，
由∠DPO＝∠POB，得DP∥OB，
∵D与P关于y轴对称，P（1，﹣3），
∴D（﹣1，﹣3）；
当点D在OP右侧时，延长PD交x轴于点G．
作PH⊥OB于点H，则OH＝1，PH＝3．
∵∠DPO＝∠POB，
∴PG＝OG．
设OG＝x，则PG＝x，HG＝x﹣1．
在Rt△PGH中，由x2＝（x﹣1）2+32，得x＝5．
∴点G（5，0）．
∴直线PG的解析式为y＝x﹣②，
联立①②并解得：，
∵P（1，﹣3），
∴D（，﹣）．
∴点D的坐标为（﹣1，﹣3）或D（，﹣）；


（2）点P运动时，是定值，定值为2，理由如下：

过点P作PQ⊥AB于Q点，设P（m，am2+c），A（﹣t，0），B（t，0），则at2+c＝0，c＝﹣at2．
∵PQ∥OF，
∴，
∴FO＝＝＝amt+at2．
同理OE＝﹣amt+at2．
∴OE+OF＝2at2＝﹣2c＝2OC．
∴．
在Rt△AOE中，tan∠PAB＝，
在Rt△BOF中，tan∠PBA＝，
在Rt△AOC中，tan∠OAC＝，
∴＝．
【点评】本题考查了二次函数综合题，①利用待定系数法求函数解析式；②利用函数值相等的点关于对称轴对称得出D点坐标是解题关键；（2）利用待定系数法求出E、F点坐标是解题关键．