人教版八年级上册12.3 角的平分线的性质练习题

这是一份人教版八年级上册12.3 角的平分线的性质练习题，共14页。
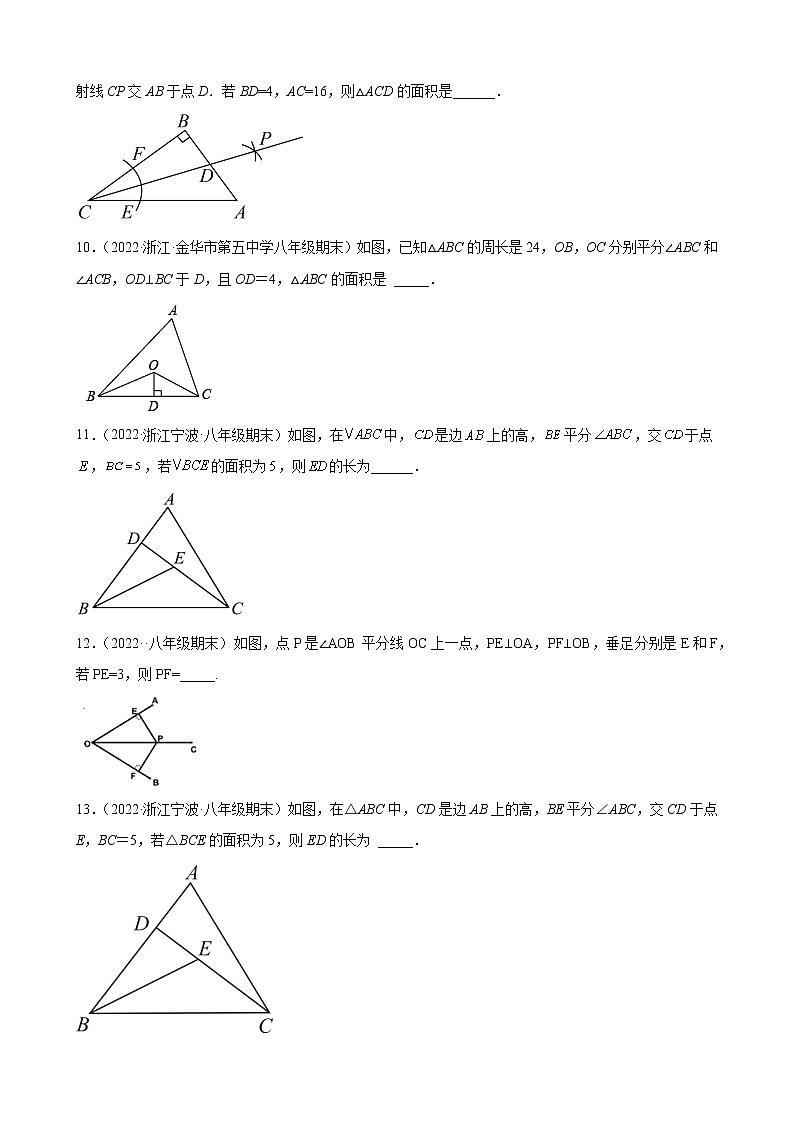
12.3 角的平分线的性质 1．（2022·浙江台州·八年级期末）如图，OP平分∠AOB，E为OA上一点，OE＝4，P到OB的距离是2，则△OPE的面积为（    ）A．2 B．3 C．4 D．82．（2022·浙江绍兴·八年级期末）如图，，BP和CP分别平分∠ABC和∠BCD，AD过点P，且与AB垂直．若，，则BCP的面积为（    ）A．16 B．20 C．40 D．803．（2022·浙江杭州·八年级期末）下列语句中是命题的有（    ）①线段垂直平分线上的点到线段两端的距离相等；②作点A关于直线l的对称点③三边对应相等的两个三角形全等吗？④角平分线上的点到角两边的距离相等．A．1个 B．2个 C．3个 D．4个4．（2022·浙江丽水·八年级期末）下列命题中，是真命题的是（    ）A．对应角相等的两个三角形是全等三角形．B．三个内角之比为3:4:5的三角形是直角三角形．C．平面直角坐标系中，点的横坐标是点到x轴的距离．D．角平分线上的点到角两边的距离相等．5．（2022·浙江丽水·八年级期末）如图，，点E是AD上的点，连接BE，CE，且，BE平分．以下结论中：①E是AD中点，②，③，④，正确的个数为（    ）A．4 B．3 C．2 D．16．（2022·浙江宁波·八年级期末）如图是用直尺和圆规作已知角∠AOB平分线OP的示意图，仔细观察，根据三角形全等的知识，说明画出OP的依据是（    ）A．边角边，全等三角形对应角相等B．角边角，全等三角形对应角相等C．边边边，全等三角形对应角相等D．斜边直角边，全等三角形对应角相等7．（2022·浙江丽水·八年级期末）如图是用尺规作一个角的平分线，其依据正确的是（    ）A．SAS B．SSS C．AAS D．ASA8．（2022·浙江金华·八年级期末）如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上一个动点，若PA=3，则PQ的最小值为_____．9．（2022·浙江金华·八年级期末）如图，在Rt△ABC中，∠B=90°，以顶点C为圆心、适当长为半径画弧，分别交AC、BC于点E、F，再分别以点E、F为圆心，以大于EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D．若BD=4，AC=16，则△ACD的面积是______．10．（2022·浙江·金华市第五中学八年级期末）如图，已知△ABC的周长是24，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝4，△ABC的面积是 _____．11．（2022·浙江宁波·八年级期末）如图，在中，是边上的高，平分，交于点，，若的面积为，则的长为______．12．（2022··八年级期末）如图，点P是∠AOB平分线OC上一点，PE⊥OA，PF⊥OB，垂足分别是E和F，若PE=3，则PF=_____.  13．（2022·浙江宁波·八年级期末）如图，在△ABC中，CD是边AB上的高，BE平分∠ABC，交CD于点E，BC＝5，若△BCE的面积为5，则ED的长为 _____．14．（2022·浙江台州·八年级期末）如图，在中，是的平分线，延长至点，使，连接，若，的面积为1，则的面积是______．15．（2022·浙江·杭州外国语学校八年级期末）平面直角坐标系xOy中有点P（x，y），实数x，y，m满足以下两个等式：2x﹣3m＋1＝0，3y﹣2m﹣16＝0．(1)当x＝1时，点P到x轴的距离为        ；(2)若点P落在一、三象限的角平分线上，求点P的坐标；(3)当x≤4＜y时，求m的最小整数值．16．（2022·浙江绍兴·八年级期末）如图，已知ABC．(1)请用直尺和圆规作∠ABC的角平分线BD，交AC于点D．（保留作图痕迹，不写作法）(2)在（1）的条件下，若，，求∠BDA的度数．
参考答案：1．C【解析】根据角平分线上的点到角的两边距离相等，求得△OPE的OE边上的高，即可求得△OPE的面积．如图，作PH⊥OA于点H，∵OP平分∠AOB，P到OB的距离是2，∴PH=2∴△OPE的面积为，∴△OPE的面积为4，故选：C本题考查了角平分线的性质定理，熟练掌握定理的内容是解答此题的关键所在．2．B【解析】过点P作PE⊥BC于E，根据角平分线上的点到角的两边的距离相等可得PA=PE，PD=PE，那么PE=PA=PD，又AD=8，进而求出PE=4，进而根据三角形面积公式求解即可．解：过点P作PE⊥BC于E，∵AB∥CD，PA⊥AB，∴PD⊥CD，∵BP和CP分别平分∠ABC和∠BCD，∴PA=PE，PD=PE，∴PE=PA=PD，∵PA+PD=AD=8，∴PA=PD=4，∴PE=4．故选：B．本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质并作辅助线是解题的关键．3．B【解析】根据命题的定义分别进行判断即可．解：①线段垂直平分线上的点到线段两端的距离相等，是命题；②作点A关于直线l的对称点A'，不是命题；③三边对应相等的两个三角形全等吗？不是命题；④角平分线上的点到角两边的距离相等，是命题；故选：B．本题考查了命题与定理：判断事物的语句叫命题，命题有题设与结论两部分组成；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．4．D【解析】根据全等三角形的判定定理、三角形内角和定理、点的坐标、角平分线的性质进行判断即可．A：对应角相等的两个三角形不一定是全等三角形，本选项错误不符合题意；B：设三个内角分别为3x、4x、5x，则3x+4x+5x=180°，解得x=15°，则三个内角分别为：45°、60°、75°，∴三个内角之比为3:4:5的三角形不是直角三角形，本选项错误不符合题意；C：平面直角坐标系中，点的横坐标的绝对值是点到y轴的距离，本选项错误不符合题意；D：角平分线上的点到角两边的距离相等，本选项正确符合题意；故选：D．本题考查的是命题的真假判断，全等三角形的判定、三角形内角和定理、点的坐标、角平分线的性质，熟记这些性质是解题的关键．5．B【解析】延长BE交CD的延长线于点F，证明∆ABE≅∆DFE，得出AE=DE，AB=DF，即可判断①和②正确；过点E作EM⊥BC于点M，EN⊥CD于点N，由角平分线的性质定理即可判断③④．解：延长BE交CD的延长线于点F，∵AB∥CD，∴∠ABE=∠F，∵BE平分∠ABC，∴∠ABE=∠CBE，∴∠F=∠CBE，∴CF=BC，∵∠BEC=90°，∴CE⊥BF，∴∠BCE=∠FCE，BE=EF，∵∠AEB=∠FED，∴∆ABE≅∆DFE，∴AE=DE，AB=DF，故①正确；∵CF=CD+DF，∴BC=CD+AB，故②正确；∵∠EDC≠∠ECD，∴ED≠EC，故③错误；过点E作EM⊥BC于点M，EN⊥CD于点N，∵CE平分∠BCD，∴EM=EN，∴，故④正确；故选：B．题目主要考查全等三角形的判定和性质，等腰三角形的性质，平行线的性质及角平分线的性质定理，熟练掌握运用这些知识点是解题关键．6．C【解析】结合题意，根据角平分线尺规作图、全等三角形的性质分析，即可得到答案．根据题意，得：， 在和中 ∴ ∴，即∴画出OP的依据是：边边边，全等三角形对应角相等故选：C．本题考查了角平分线、全等三角形的知识；解题的关键是熟练掌握角平分线尺规作图、全等三角形的性质，从而完成求解．7．B【解析】利用基本作图和三角形全等的判定方法求解．解：如图，由作法得到，，而为公共边，所以根据“”可判断，所以，即平分．故选：B．本题考查了作图基本作图，解题的关键是熟练掌握5种基本作图，也考查了全等三角形的判定．8．3【解析】由垂线段最短可知，当PQ与OM垂直的时候，PQ的值最小．解：由垂线段最短可知，当PQ与OM垂直的时候，PQ的值最小，根据角平分线的性质可知，此时PA=PQ=3．故答案为：3．本题考查了角平分线的性质，垂线段最短，解题的关键是掌握垂线段距离最短．9．32【解析】过点D作DQ⊥AC，由作法可知CP是角平分线，根据角平分线的性质知DB=DQ=3，再由三角形的面积公式计算即可．解：如图，过点D作DQ⊥AC于点Q，由作图知CP是∠ACB的平分线，∵∠B=90°，BD=4，∴DB=DQ=4，∵AC=16，∴S△ACD=•AC•DQ=，故答案为32．本题主要考查作图-基本作图，三角形面积，解题的关键是掌握角平分线的尺规作图及角平分线的性质．10．48【解析】过O作OE⊥AB于E，OF⊥AC于F，连接OA，根据角平分线的性质可得OE=OF=OD=4，再由△ABC的面积是：，即可求解．解：过O作OE⊥AB于E，OF⊥AC于F，连接OA，∵OB，OC分别平分∠ABC和∠ACB，OD⊥BC，OE⊥AB，OF⊥AC，∴OE=OD，OD=OF，即OE=OF=OD=4，∴△ABC的面积是：，故答案为：48.本题主要考查了角平分线的性质，熟练掌握角平分线上点到角两边的距离相等是解题的关键．11．2【解析】过作于，根据角平分线性质求出，根据三角形面积公式求出即可．解：过作于， 是边上的高，平分，交于点，，，，，故答案为：．本题考查了角平分线性质的应用，能根据角平分线性质求出是解此题的关键，注意：在角的内部，角平分线上的点到角的两边的距离相等．12．3.【解析】根据角平分线上的点到角两边的距离相等即可得到答案．∵点P是∠AOB平分线OC上一点，PE⊥OA，PF⊥OB ∴PF=PE=3.本题考查了角平分线的性质：角平分线上的点到角两边的距离相等．13．2【解析】过E作EF⊥BC于F，根据角平分线性质求出EF=DE=8，根据三角形面积公式求出即可．解：过E作EF⊥BC于F，∵CD是AB边上的高，BE平分∠ABC，交CD于点E，∴DE=EF，∵S△BCE=×BC×EF=5，∴×5×EF=5，∴EF=DE=2，故答案为：2．本题考查了角平分线性质的应用，能根据角平分线性质求出EF=DE=8是解此题的关键，注意：在角的内部，角平分线上的点到角的两边的距离相等．14．6【解析】由角平分线的性质可得DG＝DH，由三角形的面积关系可求解．解：如图，过点D作DG⊥AC于G，DH⊥CB于H，∵DECD，△BDE的面积为1，∴S△BCD＝2S△BDE＝2，∵CD是∠ACB的平分线，DH⊥CB，DG⊥AC，∴DG＝DH，∵AC＝2BC，，，∴S△ACD＝2S△BCD，∴S△ACD＝4，∴S△ABC＝S△ACD+S△BCD＝4+2＝6，故答案为：6．本题考查了角平分线的性质，三角形的面积公式，添加恰当辅助线是解题的关键．15．(1)6(2)P(10，10)(3)−1 【解析】（1）当x＝1时，由2x﹣3m＋1＝0可求得m的值，再由3y﹣2m﹣16＝0可求得y的值，从而可得点P的坐标，即可得点P到x轴的距离；（2）根据角平分线的性质定理及点在第一、三象限的坐标特征可得x=y，从而可得关于x与m的方程组，消去m即可求得x的值，从而可得点P的坐标；（3）由条件可得用含m的代数式表示x、y的等式，根据不等关系可得关于m的不等式组，解不等式组即可求得m的最小整数值．(1)当x＝1时，由2x﹣3m＋1＝0，得 解得m=1由3y﹣2m﹣16＝0，得 解得y=6∴点P的坐标为(1，6)即点P到x轴的距离为6故答案为：6(2)∵点P在第一、三象限的角平分线上，且在一、三象限的点的两个坐标符号相同∴ ∴3x﹣2m﹣16＝0由消去m，得x=10∴y=10∴点P的坐标(10，10)(3)由2x﹣3m＋1＝0，3y﹣2m﹣16＝0可得： 由题意得： 解不等式组得： 故不等式组的整数解为：−1，0，1，2，3，最小整数值为−1．本题考查了点与坐标，角平分线的性质定理，点在各个象限的坐标特征，解二元一次方程组及解一元一次不等式组等知识，灵活运用这些知识是关键．16．(1)见解析(2) 【解析】（1）根据尺规作图作角平分线的步骤即可完成；（2）由三角形内角和定理可求得∠ABC的度数，再由角平分线的性质可得∠DBC的度数，由三角形外角的性质即可求得结果．（1）如图（2）∵∠A＝100°，∠C＝28°，∴，又∵BD平分∠ABC，∴∠DBC＝26°，∴．本题考查了角平分线的尺规作图，角平分线的性质，三角形内角和定理及外角性质，掌握这些性质是关键．