




初中数学浙教版八年级下册4.2 平行四边形授课ppt课件
展开理解并掌握平行四边形的概念和平行四边形对边、对角 相等的性质;
会用平行四边形的性质解决简单的平行四边形的计算 问题,并会进行有关的论证;
了解平行四边形的不稳定性及其实际应用.
你知道遮阳蓬的伸缩架为什么采用平行四边形的结构吗?
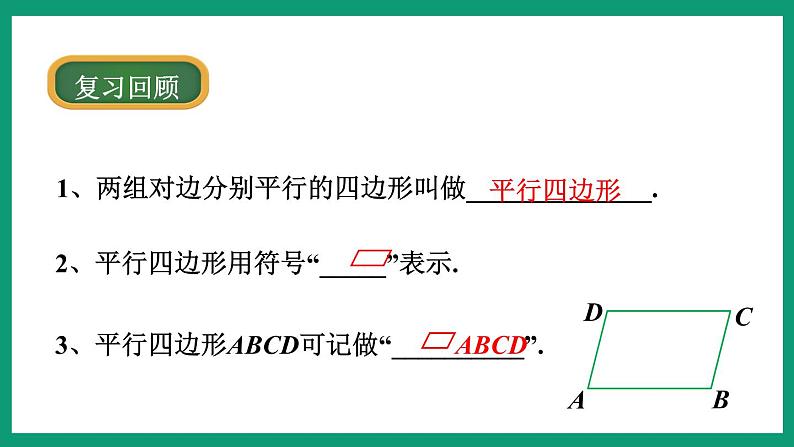
1、两组对边分别平行的四边形叫做______________.
2、平行四边形用符号“_____”表示.
3、平行四边形ABCD可记做“__________”.
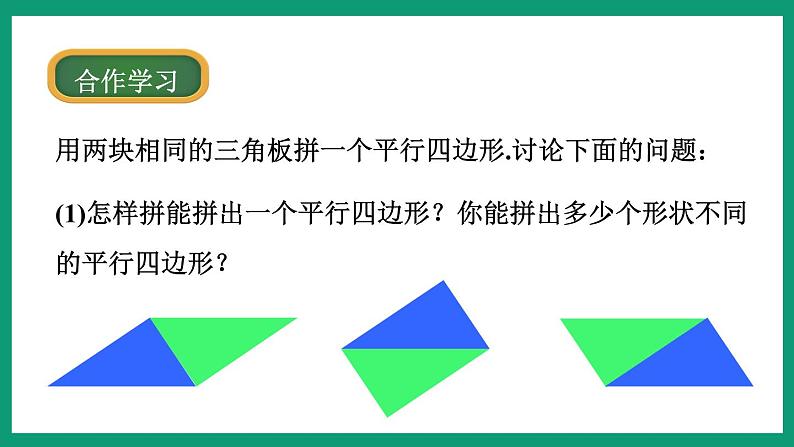
用两块相同的三角板拼一个平行四边形.讨论下面的问题:
(1)怎样拼能拼出一个平行四边形?你能拼出多少个形状不同的平行四边形?
(2)怎样证明你拼出的四边形是平行四边形?
分析:如图,△ABC≌△CDA,所以∠B=∠D, ∠CAB=∠DCA,∠ACB=∠DAC,AB=CD,BC=AD,
∵∠CAB=∠DCA,∴AB∥CD,
∵∠ACB=∠DAC,∴BC∥AD,∴四边形ABCD是平行四边形.
(3)通过上述活动,你发现平行四边形有哪些性质?你能证明这些性质吗?
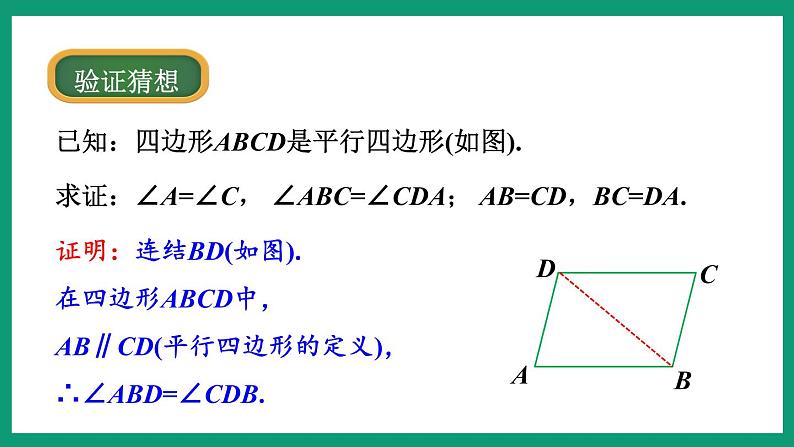
证明:连结BD(如图).在四边形ABCD中, AB∥CD(平行四边形的定义),∴∠ABD=∠CDB.
已知:四边形ABCD是平行四边形(如图).
求证:∠A=∠C, ∠ABC=∠CDA; AB=CD,BC=DA.
同理,∠ADB=∠CBD.又BD=DB,∴△ABD≌△CDB.∴AB=CD,BC=DA,∠A=∠C.同理可得,∠ABC=∠CDA.
平行四边形的对角相等.
∵四边形ABCD是平行四边形,∴∠A=∠C,∠B=∠D.
平行四边形的对边相等.
∵四边形ABCD是平行四边形,∴AB=CD,AD=BC.
AD∥BC,AD=CB(平行四边形的对边相等).
∴四边形AFCE是平行四边形(平行四边形的定义).
∴AE=CF(平行四边形的对边相等).∴AD-AE=CB-CF,即DE=BF.∵∠BAD=∠DCB,∠EAF=∠FCE(平行四边形的对角相等),∴∠BAD-∠EAF=∠DCB-∠FCE,即∠BAF=∠DCE.
∵AF∥CE,∴四边形AFCE是平行四边形,∴AF=CE,∠FAE=∠FCE,∴∠BAD-∠FAE=∠BCD-∠FCE,即∠BAF=∠DCE,
AD∥BC,∠BAD=∠BCD,
∴△BAF≌△DCE,∴BF=DE,∠BAF=∠DCE.
AB=CD,∠BAF=∠DCE, AF=CE,
在△BAF和△DCE中,
(1)若∠A=130°,则∠B=_____,∠C=_____,∠D=_____;
(2)若∠A+∠C=200°,则∠A=______,∠B=______.
做一个平行四边形,用双手捏住平行四边形的两个对角,向相反方向拉,你发现了什么?
平行四边形具有不稳定性
平行四边形的不稳定性在日常生活和生产实际中有许多应用,如衣帽架、伸缩门、可伸缩的遮阳蓬等,都反映了四边形的不稳定性的应用.
(1)若∠D=60°,∠DAC=40°,则∠B=____,∠BAC=____.
(2)若∠DAB-∠D=10°,则∠DCB-∠B=____.
A.∠1+∠2=180° B.∠2+∠3=180° C.∠3+∠4=180° D.∠2+∠4=180°
2.如图,在平行四边形ABCD中,下列各式不一定正确的是( )
3.已知:如图,在平行四边形ABCD中,E是CD上一点,BE=BC.求证:AD=BE,∠A=∠ABE.
AD=BC,AB∥CD,∵ BE=BC,∴ AD=BE.
∵AB∥CD,∴∠ABE=∠CEB.在△BEC中,BE=BC,所以∠CEB=∠C.又∵∠A=∠C,∴∠A=∠CEB,即∠A=∠ABE.
沪科版八年级下册19.2 平行四边形背景图课件ppt: 这是一份沪科版八年级下册19.2 平行四边形背景图课件ppt,共11页。PPT课件主要包含了平行四边形,平行四边形的性质,提高题等内容,欢迎下载使用。
浙教版八年级上册4.2 平面直角坐标系优秀ppt课件: 这是一份浙教版八年级上册4.2 平面直角坐标系优秀ppt课件,文件包含浙教版数学八上421认识平面直角坐标系课件pptx、浙教版数学八上42平面直角坐标系练习docx、浙教版数学八上421认识平面直角坐标系教案doc等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
初中数学浙教版八年级上册4.2 平面直角坐标系完美版课件ppt: 这是一份初中数学浙教版八年级上册4.2 平面直角坐标系完美版课件ppt,共31页。PPT课件主要包含了学习目标,情景导入,问题思考,问题解决,知识精讲,针对练习,典例解析,m>2,1-2,达标检测等内容,欢迎下载使用。














