


浙教版八年级下册第四章 平行四边形4.4 平行四边形的判定课文配套课件ppt
展开理解并掌握平行四边形的两个判定定理,并会应用它们判断一个四边形是不是平行四边形.会根据平行四边形的定义判定四边形是否为平行四边形.
1. 平行四边形的定义是什么?
两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质有哪些?
平行四边形是中心对称图形,它的对称中心是两条对角线的交点.
平行四边形的对边相等,对角相等.
平行四边形的对角线互相平分.
平行四边形的一个判定方法.
平行四边形还有什么判定方法?
取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
猜想:一组对边平行且相等的四边形是平行四边形.
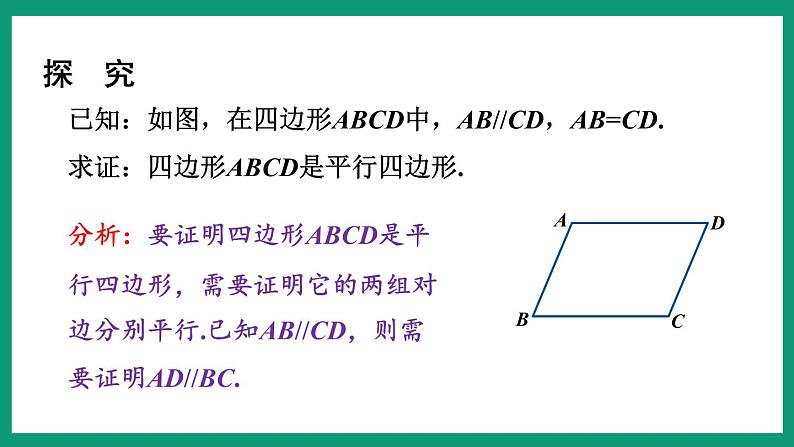
已知:如图,在四边形ABCD中,AB//CD,AB=CD.求证:四边形ABCD是平行四边形.
分析:要证明四边形ABCD是平行四边形,需要证明它的两组对边分别平行.已知AB//CD,则需要证明AD//BC.
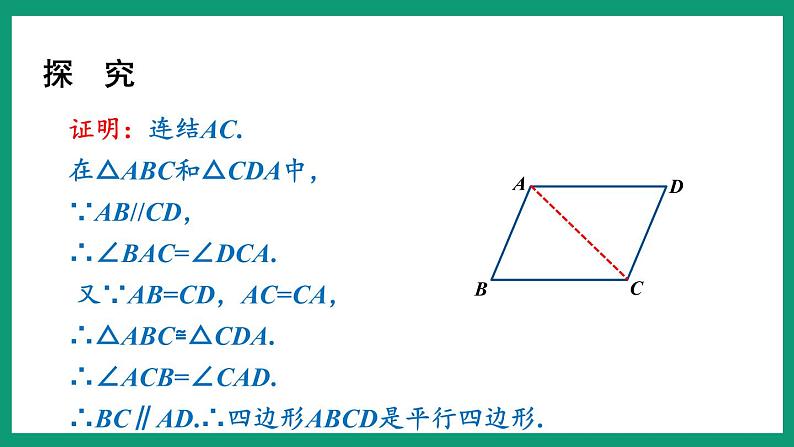
证明:连结AC.在△ABC和△CDA中,∵AB//CD,∴∠BAC=∠DCA. 又∵AB=CD,AC=CA,∴△ABC≌△CDA.∴∠ACB=∠CAD.∴BC∥AD.∴四边形ABCD是平行四边形.
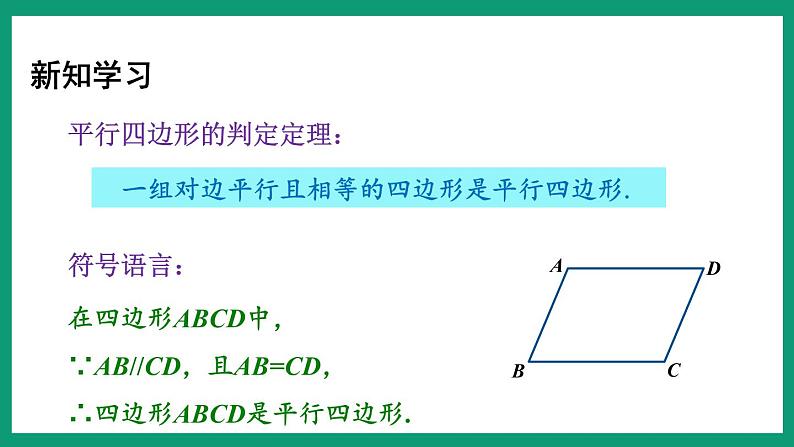
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
在四边形ABCD中,∵AB//CD,且AB=CD,∴四边形ABCD是平行四边形.
一组对边平行,另一组对边相等的四边形是平行四边形吗?若是,请说明理由;若不是,请举出反例.
AD∥BC且AB=DC,但四边形ABCD不是平行四边形.
不是.反例:等腰梯形.
两组对边分别相等的四边形是平行四边形吗?
分析:通过辅助线可以把四边形ABCD分成两个三角形,证明两个三角形全等,从而证明该四边形为平行四边形.
已知:如图,四边形ABCD中,AB=CD, AD=BC .求证:四边形ABCD是平行四边形.
∴△ABC≌△CDA,
∴∠CAB=∠ACD, ∴AB ∥ CD.又∵AB=CD,
∴四边形ABCD是平行四边形.
平行四边形的判定定理:两组对边分别相等的四边形是平行四边形.
在四边形ABCD中,∵AB=CD,且AD=BC,∴四边形ABCD是平行四边形.
1.已知:如图,AC//ED,点B在AC上,且AB=ED=BC,找出图中的平行四边形,并说明理由.
解:∵AB∥ED,且AB=ED,∴四边形ABDE是平行四边形.∵BC∥ED,且BC=ED,∴四边形BCDE是平行四边形.
2.已知:平行四边形ABCD中,E、F分别是边AD、BC的中点,求证:EB=DF.
目前,我们学习了哪些判定平行四边形的方法?
方法一:根据平行四边形的定义,满足条件“两组对边分别平行的四边形是平行四边形”.
方法二:根据平行四边形的判定定理,满足条件“一组对边平行且相等的四边形是平行四边形”.
方法三:根据平行四边形的判定定理,满足条件“两组对边分别相等的四边形是平行四边形”.
人教版八年级下册18.1.2 平行四边形的判定多媒体教学ppt课件: 这是一份人教版八年级下册18.1.2 平行四边形的判定多媒体教学ppt课件,共20页。PPT课件主要包含了开启记忆之门,平行四边形的对角相等,☆找平行四边形,☆构造平行四边形,当堂检测,画一画,泸州中考题,cm或12cm,数学复习课的主要任务等内容,欢迎下载使用。
浙教版九年级上册4.3 相似三角形优质ppt课件: 这是一份浙教版九年级上册4.3 相似三角形优质ppt课件,共19页。PPT课件主要包含了学习目标,情景引入,知识精讲,符号语言,典例解析,∴∠AED=∠C,∠A=∠FEC,针对练习,达标检测,ACD等内容,欢迎下载使用。
初中数学浙教版七年级上册4.4 整式精品ppt课件: 这是一份初中数学浙教版七年级上册4.4 整式精品ppt课件,共17页。PPT课件主要包含了v×t,5×x,πr2,m×m,-3x2y3,-3xy3,-3x2y2,-3x3y等内容,欢迎下载使用。













