浙教版八年级下册4.6 反证法课文ppt课件

这是一份浙教版八年级下册4.6 反证法课文ppt课件，共21页。PPT课件主要包含了假设“李子甜”，假设不成立，练一练，直接证明，几何语言，∴l1∥l3，在同一平面内等内容，欢迎下载使用。
通过实例，体会反证法的含义；
了解反证法的步骤，会用反证法证明简单的命题.
根据路边的李树上结满了成熟的果子，有人推断这棵树上李子的味道一定是苦的.你认为有道理吗？为什么？
中国古代有一个叫《路边苦李》的故事：王戎7岁时，与小伙伴们外出游玩，看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子，只有王戎站在原地不动.有人问王戎为什么，王戎回答说:“树在道边而多子，此必苦李.”小伙伴摘取李子尝了一下，果然是苦李.
王戎是怎样知道李子是苦的？他运用了怎样的推理方法？
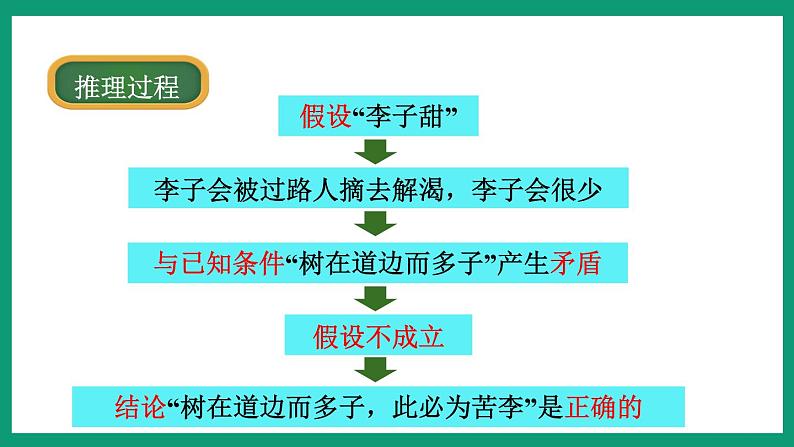
李子会被过路人摘去解渴，李子会很少
与已知条件“树在道边而多子”产生矛盾
结论“树在道边而多子，此必为苦李”是正确的
上述所用方法和之前使用的方法有什么区别？
上面的过程，是先假设命题不成立，从这样的假设出发，经过推理得出和已知条件矛盾，从而得出假设命题不成立是错误的，即所求证的命题正确.
先假设命题不成立，从这样的假设出发，经过推理得出和已知条件矛盾，或者与定义、基本事实、定理等矛盾，从而得出假设命题不成立是错误，即所求证的命题正确.这种证明方法叫做反证法．
2、运用反证法证明命题的一般步骤：
(1)否定结论：假设命题的结论不成立；
(2)推出矛盾：从这个假设出发，经过推理得出和已知条件矛盾，或者与定义、基本事实、定理等矛盾；
(3)肯定结论：由矛盾判定假设命题不成立是错误的，即所求证的命题正确.
证明：假设四边形ABCD中没有一个角是钝角或直角，即∠A＜90°，∠B＜90°，
例 求证：四边形中至少有一个角是钝角或直角.
已知：四边形ABCD(如图).求证：四边形ABCD中至少有一个角是钝角或直角.
∠C＜90°，∠D＜90°，于是∠A+∠B +∠C+∠D＜360°.这与“四边形的内角和为360°”矛盾.所以四边形ABCD中至少有一个角是钝角或直角.
用反证法证明“△ABC中，若∠A＞∠B＞∠C，则∠A＞60°”，第一步应假设( )　　A．∠A=60°B．∠A＜60°C．∠A≠60°D．∠A≤60°
解析：∠A与60°的大小关系有∠A＞60°，∠A=60°，∠A＜60°三种情况，因而∠A＞60°的反面是∠A≤60°．因此应先假设∠A≤60°．
求证：在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线也互相平行.
(1)你会选择哪一种证明方法？
(2)如果你选择反证法，先怎样假设？结果和什么产生矛盾？
已知:如图，l1∥l2 ，l2 ∥l3 .求证：l1∥l3 .
证明:作直线l交直线l2于点p，
∵l1∥l2，l2∥l3 ，
∴∠2 =∠1=∠3，∴ l1∥l3 (同位角相等，两直线平行).
∴直线l必定与直线l1，l3相交(在同一平面内，如果一条直线和两条平行直线中的一条相交，那么和另一条直线也相交)，
分析：假设l1不平行l3，则l1与l3相交，设交点为p.因为l1∥l2，l2∥l3 ，则过点p就有两条直线l1、 l3都与l2平行，这与“经过直线外一点，有且只有一条直线平行于已知直线”矛盾．
定理:在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线也互相平行.
1、用反证法证明(填空):两直线平行，同位角相等.已知：如图，直线l1，l2被l3所截，A，B为交点， l1∥l2.求证：∠1＝∠2.
证明:假设所求证的结论不成立，即_______≠_______.
过点A作直线l4，使l4与l3所成的∠3与∠2相等，
又已知 l1∥l2 ，这与基本事实“_________________________________________________________________________”产生矛盾.所以_________不成立.所求证的结论成立.
则∠3______∠1，所以直线l4与直线l1不重合.但l4∥l2( ______________________________)，
同位角相等，两直线平行
如果两条直线都和第三条直线平行，
那么这两条直线也互相平行
2、用反证法证明在同一平面内，若a⊥b，a⊥c，则b∥c时，第一步应假设(　　)A．b不平行于c B．a不垂直于cC．a不垂直于b D．b平行于c
3、用反证法证明: 如果a·b=0，那么a，b中至少有一个等于0.
已知： a·b=0．求证：a=0或b=0． 证明：假设a ≠0且b ≠0，则ab≠0，与已知相矛盾，∴假设a ≠0且b ≠0不成立，∴如果ab=0，那么a，b中至少有一个等于0.