浙教版八年级下册5.2 菱形教学ppt课件

这是一份浙教版八年级下册5.2 菱形教学ppt课件，共20页。PPT课件主要包含了学习目标，菱形的四条边都相等，温故知新，四条边相等，对角线互相垂直，如何证明以上定理，∴ABCD是菱形，例题讲解，随堂练习，课堂小结等内容，欢迎下载使用。

经历菱形判定定理的探究过程，掌握菱形的判定定理．会用这些菱形的判定方法进行有关的证明和计算.
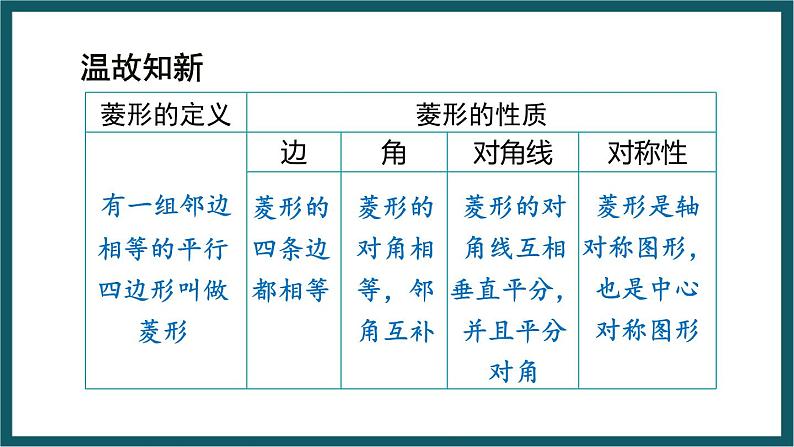
有一组邻边相等的平行四边形叫做菱形
菱形的对角相等，邻角互补
菱形的对角线互相垂直平分，并且平分对角
菱形是轴对称图形，也是中心对称图形
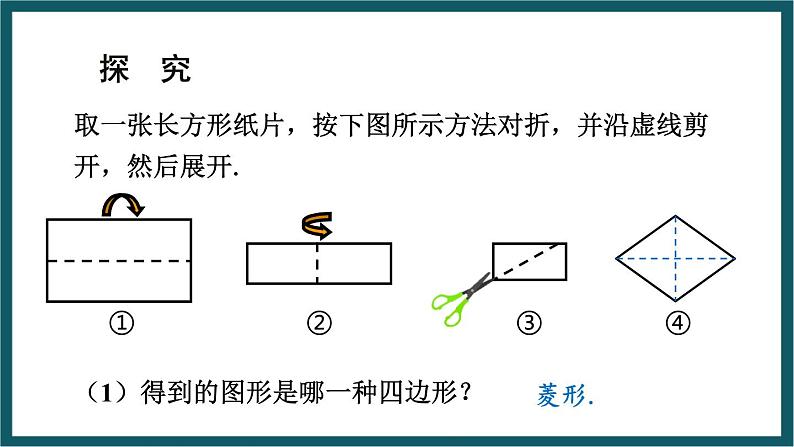
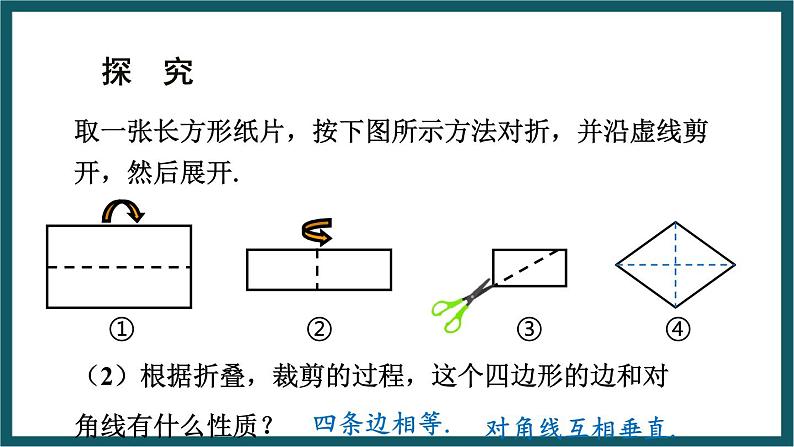
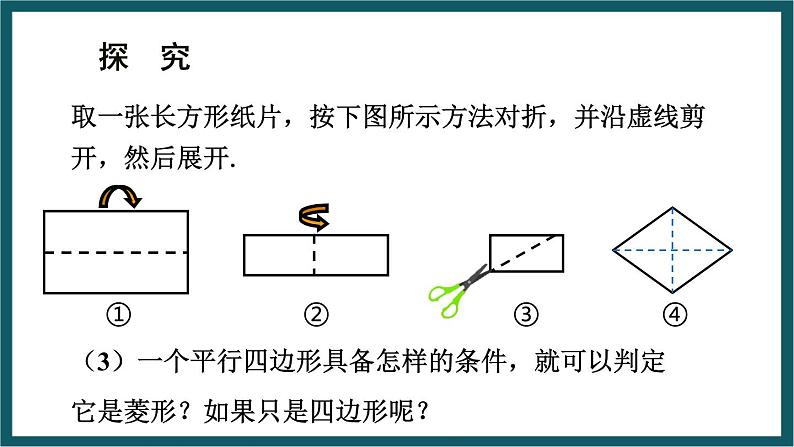
取一张长方形纸片，按下图所示方法对折，并沿虚线剪开，然后展开.
（1）得到的图形是哪一种四边形？
（2）根据折叠，裁剪的过程，这个四边形的边和对角线有什么性质？
（3）一个平行四边形具备怎样的条件，就可以判定它是菱形？如果只是四边形呢？
一般地，判定菱形有以下的定理：
定理1 四条边相等的四边形是菱形.定理2 对角线互相垂直的平行四边形是菱形.
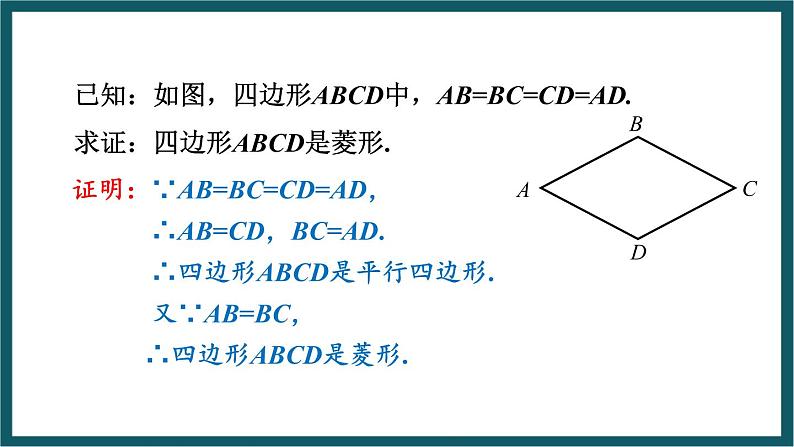
证明：∵AB=BC=CD=AD， ∴AB=CD，BC=AD. ∴四边形ABCD是平行四边形. 又∵AB=BC， ∴四边形ABCD是菱形.
已知：如图，四边形ABCD中，AB=BC=CD=AD.求证：四边形ABCD是菱形.
几何语言：∵在四边形ABCD中，AB=BC=CD=AD，∴四边形 ABCD是菱形.
分析：我们可根据菱形的定义来证明这个平行四边形是菱形，由平行四边形的性质得到BO=DO，由∠AOB=∠AOD=90º及AO=AO，得△AOB≌△AOD，可得到AB=AD (或根据线段垂直平分线性质定理，得到AB=AD) ，最后证得ABCD是菱形.
已知：在ABCD中，对角线AC⊥BD，求证：ABCD是菱形.
∵四边形ABCD是平行四边形，∴OB=OD(平行四边形的对角线互相平分).∵ AC⊥BD，∴AC为线段BD的垂直平分线.∴BA=AD (线段垂直平分线的性质).
几何语言：∵在ABCD中，AC⊥BD，∴ABCD是菱形.
例1 如图，在矩形ABCD中，对角线AC的垂直平分线与边AD、BC分别交于点E、F，求证：四边形AFCE是菱形 .
证明：∵四边形ABCD是矩形，∴AE∥CF(矩形的定义).∴∠1＝∠2．又∵∠AOE＝∠COF，AO＝CO．
∴△AOE≌△COF，∴EO＝FO，
∴ 四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形). 又∵EF⊥AC，∴ 四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
1.如图所示，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，两弧相交于点C，D，则直线CD即为所求.连接AC，BC，AD，BD，根据她的作图方法可知，四边形ADBC一定是(　　)A．矩形 B．菱形C．正方形　　　 D．等腰梯形
解析：由题意知AC=AD=BD=BC，∴四边形ADBC一定是菱形.
2.如图，AD是△ABC的一条角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F.求证：四边形AEDF是菱形.
证明：∵DE∥AC，DF∥AB， ∴四边形AEDF是平行四边形 且∠EDA=∠DAF. ∵AD是△ABC的一条角平分线， ∴∠EAD=∠DAF.
∴∠EDA=∠EAD，∴EA=ED.∴四边形AEDF是菱形.
定理1 四条边相等的四边形是菱形
定理2 对角线互相垂直的平行四边形是菱形
定义法：有一组邻边相等的平行四边形叫做菱形
∵AB=BC=CD=AD ， ∴四边形ABCD是菱形
∵四边形ABCD是平行四边形，AB=BC，∴四边形ABCD是菱形
∵四边形ABCD是平行四边形，AC⊥BD，∴四边形ABCD是菱形