初中数学浙教版八年级下册5.3 正方形课堂教学课件ppt

这是一份初中数学浙教版八年级下册5.3 正方形课堂教学课件ppt，共18页。PPT课件主要包含了学习目标，有一个角是直角，有一组邻边相等，温故知新，新知学习，正方形的判定定理，新知巩固，∴CFFD，∵CD平分∠ACB，又∠ACB90°等内容，欢迎下载使用。

掌握正方形的概念并了解正方形与矩形、菱形的关系.探索并证明正方形的判定定理，进一步发展推理能力.体会探索与证明过程中所蕴含的抽象、推理等数学思想.
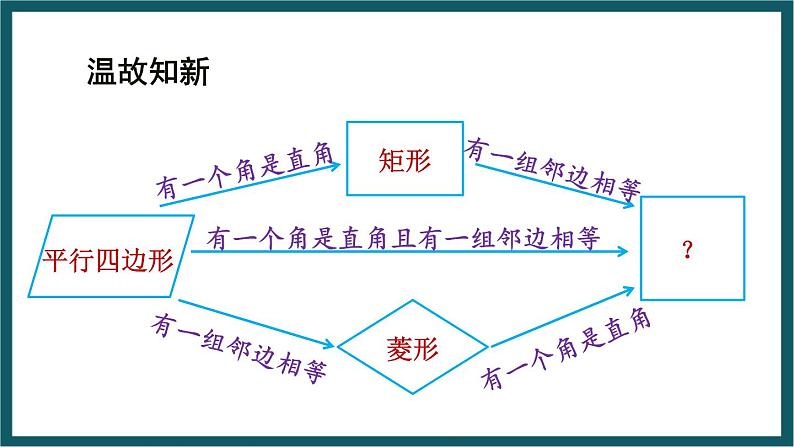
有一个角是直角且有一组邻边相等
我们把有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形.正方形既是特殊的矩形，又是特殊的菱形.
根据正方形的定义，你能说出正方形的判定方法吗？
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
还有其他方法判定正方形吗？
对角线相等的菱形是正方形.
对角线互相垂直的矩形是正方形.
判定一个四边形是正方形，只要判定这个四边形既是矩形又是菱形即可.
判断对错：(1)对角线互相垂直且相等的平行四边形是正方形.(2)对角线互相垂直的矩形是正方形.(3)对角线相等的菱形是正方形.(4)对角线互相垂直，一个角是直角的四边形是正方形.(5)对角线互相垂直平分且相等的四边形是正方形.
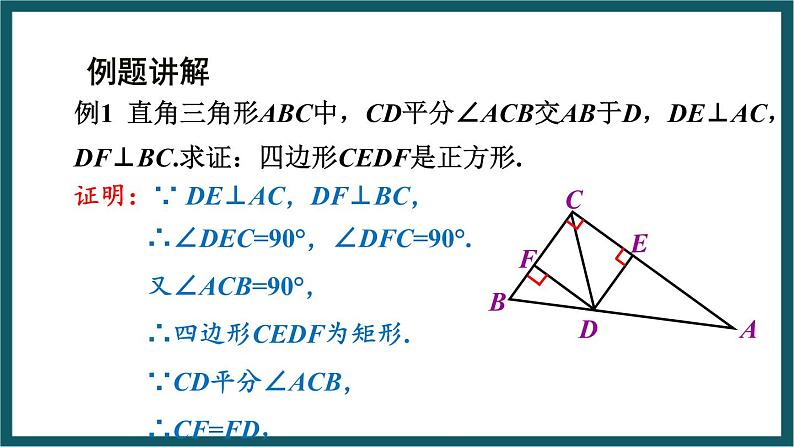
例1 直角三角形ABC中，CD平分∠ACB交AB于D，DE⊥AC，DF⊥BC.求证：四边形CEDF是正方形.
∴四边形CEDF为矩形.
∴∠DEC=90°，∠DFC=90°.
证明：∵ DE⊥AC，DF⊥BC，
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
依次连结正方形的各边中点，得到的是什么图形？
2.如图，四边形ABCD中，∠ABC=∠BCD=∠CDA=90°，请添加一个条件____________________，可得出该四边形是正方形．
AB=BC(答案不唯一)
1.  ABCD是正方形须加的条件是（ ）
A.对角线互相垂直且相等 B.对角线相等C.一组邻边相等 D.对角互补
3.如图，已知在ABCD中，对角线AC，BD交于点O，E是BD的延长线上的点，且EA=EC.(1)求证：四边形ABCD是菱形；(2)若∠DAC=∠EAD+∠AED，求证：四边形ABCD是正方形．
3.如图，已知在ABCD中，对角线AC，BD交于点O，E是BD的延长线上的点，且EA=EC.(1)求证：四边形ABCD是菱形；
证明：(1)∵四边形ABCD是平行四边形， ∴AO=CO， ∵EA=EC， ∴EO⊥AC，即BD⊥AC， ∴四边形ABCD是菱形．
3.如图，已知在ABCD中，对角线AC，BD交于点O，E是BD的延长线上的点，且EA=EC.(2)若∠DAC=∠EAD+∠AED，求证：四边形ABCD是正方形．
(2) ∵∠ADO=∠EAD+∠AED，∠DAC=∠EAD+∠AED， ∴∠ADO=∠DAC，∴AO=DO， ∵四边形ABCD是菱形， ∴AC=2AO，BD=2DO， ∴AC=BD，∴四边形ABCD是正方形.
四边形、平行四边形、矩形、菱形和正方形的关系：
正方形的判定方法：(1)从四边形出发：①有四条边相等，四个角都是直角的四边形是正方形；②对角线互相平分、垂直且相等的四边形是正方形；(2)从平行四边形出发：①有一组邻边相等并且有一个角是直角的平行四边形是正方形；②对角线互相垂直且相等的平行四边形是正方形；
(3)从矩形出发：①有一组邻边相等的矩形是正方形；②对角线互相垂直的矩形是正方形；(4)从菱形出发：①有一个角是直角的菱形是正方形；②对角线相等的菱形是正方形．