北师大版八年级上册6 实数教学课件ppt

这是一份北师大版八年级上册6 实数教学课件ppt，共27页。PPT课件主要包含了学习目标，知识回顾，问题探究，问题总结，整数或分数，1按定义分类，2按性质分类，考点1，有理数，无理数等内容，欢迎下载使用。
1、了解在有理数范围内的运算及运算法则、运算性质等在实数内仍然成立。
2、能熟练地进行实数运算。
3、在实数运算时，根据问题的要求取其近似值，转化有理数计算。
了解实数与数轴一一对应，能熟练进行实数运算
在有理数范围内的运算及运算法则、运算性质等在实数范围内成立，并按要求分类。
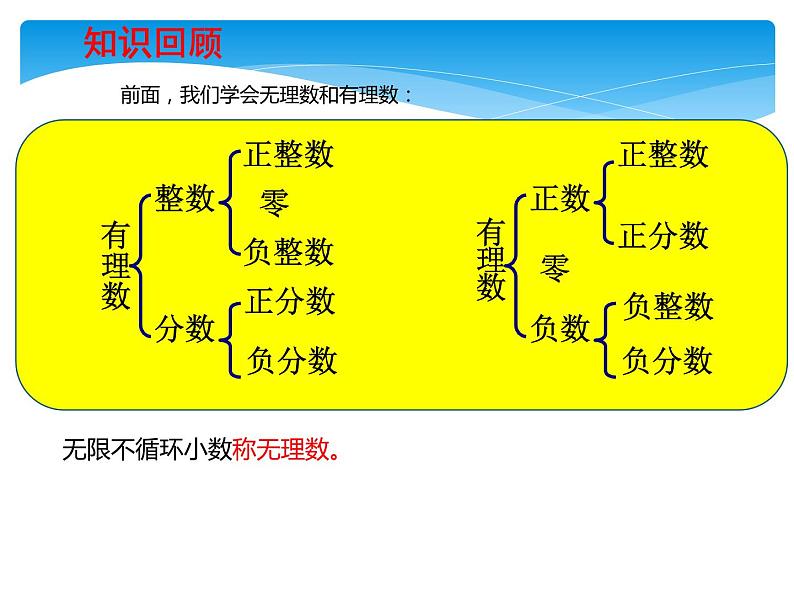
前面，我们学会无理数和有理数：
无限不循环小数称无理数。
同学们，你能进行分类吗?
0.3030030003···
问题1：我们知道有理数按定义分类包括整数和分数，现将下列分数写成小数的形式，有什么特征？
他们可以化为有限小数和无限循环小数
问题2：整数能写成小数的形式吗？3可以看成3.0吗？
思考：由此你可以得到什么结论吗？
有理数可以化为有限小数和无限循环小数的形式反过来，有理数可以化为有限小数和无限循环小数的形式
想一想：所有的数都可以数都可以写成有限小数和无限循环小数的形式吗？如：
无限不循环小数为无理数。
因此我们将实数分为有理数和无理数，仿照有理数的分类，你能给实数分类吗？
有理数：有限小数或无限循环小数
无理数：无限不循环小数
1.含开放不尽的数2.含有π的数3.有规律但不循环的小数
你能将下列各数在数轴上表示出来吗？
通过上面的问题，我们知道实数也可以在数轴上表示出来。
正实数：正有理数和正无理数
负实数：负有理数和负无理数
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全相同。
你还能举出其他的例子吗？
问题：在有理数范围内，能进行哪些运算？判断下列各式成立吗？
有理数的运算及运算律对实数仍然成立。
例1.求下列各数的相反数、倒数和绝对值：
（1）a是一个实数，它的相反数为 。 绝对值为 。（2）如果a≠0,那么它的倒数为 。
-2 -1 0 1 2
你能画出一个无理数吗?
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。 即实数和数轴上的点是一一对应的。 在数轴上的两个点，右边的点表示的实数总比左边的点表示的实数大。
1.实数不是有理数就是无理数。（ ）
2.无理数都是无限不循环小数。（ ）
3.无理数都是无限小数。（ ）
4.带根号的数都是无理数。（ ）
5.无理数一定都带根号。（ ）
6.两个无理数之积不一定是无理数。（ ）
7.两个无理数之和一定是无理数。（ ）
关于实数的计算：1、能将实数进行分类2、确定一个数的相反数，倒数，绝对值3、根据有理数的运算法则及运算性质对实数进行计算4、会画出无理数
考点一：将实数分类熟悉实数的2种分类考点二：实数的相关计算综合运用运算律解决问题考点三：会求相反数、倒数、绝对值
1.实数按定义分类：有理数和无理数2.实数按性质分类：正实数，0，负实数3.相反数和绝对值，倒数4. 利用运算律解决实数问题