2022-2023学年陕西省西安市新城区八年级（上）期中数学试卷(解析版)

这是一份2022-2023学年陕西省西安市新城区八年级（上）期中数学试卷(解析版)

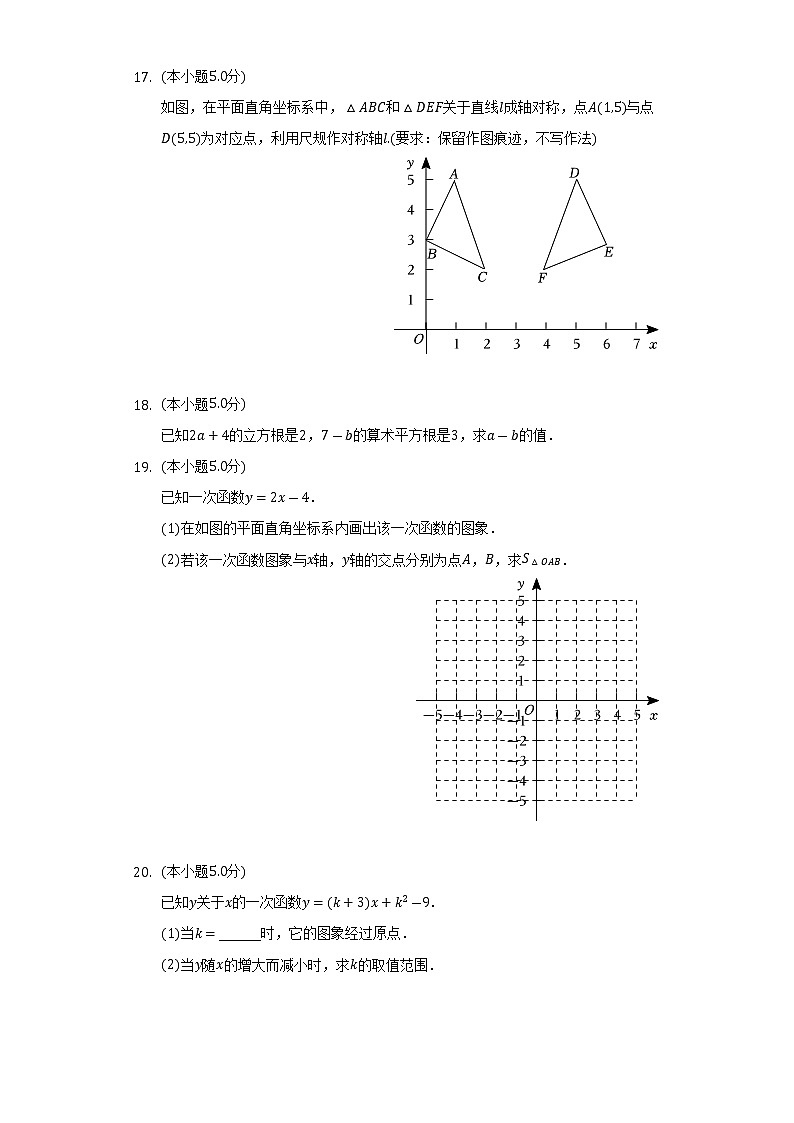
2022-2023学年陕西省西安市新城区八年级（上）期中数学试卷第I卷（选择题）一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）下列实数中，是无理数的是(    )A. 0.3 B. 2 C. 23 D. 1在平面直角坐标系中，下列各点在第二象限的是(    )A. (-3,-2) B. (2,3) C. (3,-2) D. (-2,4)以2，3为直角边的直角三角形斜边长为(    )A. 5 B. 13 C. 4 D. 5若点M(2a,-1)与点N(4,-b)关于x轴对称，则a+b的值为(    )A. -3 B. -1 C. 1 D. 3线段AB在平面直角坐标系中的位置如图所示，A(-1,4)，B(-5,1)，线段AB的长为(    )A. 5 B. 42 C. 4 D. 3将直线y=3x-1向下平移5个单位长度后与x轴的交点坐标为(    )A. (0,-6) B. (-43,0) C. (53,0) D. (2,0)估计5+1的值，应在(    )A. 1和2之间 B. 2和3之间 C. 3和4之间 D. 4和5之间如图，直线l：y=12x+m交x轴于点A，交y轴于点B(0,1)，点P(n,2)在直线l上，已知M是x轴上的动点．当以A，P，M为顶点的三角形是直角三角形时，点M的坐标为(    )A. (-2,0)或(3,0)B. (2,0)或(3,0)C. (1,0)或(4,0)D. (2,0)或(4,0)第II卷（非选择题）二、填空题（本大题共5小题，共15.0分）化简：43= ______ ．若(0,y1)，(-2,y2)为直线y=-x-5上的两个点，则y1，y2的大小关系是y1______y2(填“>”、“=”或“<”)．若点(3m-6,4+2m)在x轴上，则m=______．已知点A(-2,m)在一次函数y=2x-3的图象上，若点A也在正比例函数y=kx的图象上，则k=______．如图，在△ABC中，∠ACB=90°，AC=3，BC=4，D是AC上一点，连接BD，沿BD将△ABD折叠，若点A的对应点A'落在BC的延长线上，则折痕BD=______．三、解答题（本大题共13小题，共81.0分。解答应写出文字说明，证明过程或演算步骤）(本小题5.0分)计算：32×6-313-27．(本小题5.0分)已知2x2-8=0，求x的值．(本小题5.0分)已知点P(-3a-5,a+3)，点Q(-1,-3)，若直线PQ//x轴，求点P的坐标．(本小题5.0分)如图，在平面直角坐标系中，△ABC和△DEF关于直线l成轴对称，点A(1,5)与点D(5,5)为对应点，利用尺规作对称轴l.(要求：保留作图痕迹，不写作法)(本小题5.0分)已知2a+4的立方根是2，7-b的算术平方根是3，求a-b的值．(本小题5.0分)已知一次函数y=2x-4．(1)在如图的平面直角坐标系内画出该一次函数的图象．(2)若该一次函数图象与x轴，y轴的交点分别为点A，B，求S△OAB．(本小题5.0分)已知y关于x的一次函数y=(k+3)x+k2-9．(1)当k=______时，它的图象经过原点．(2)当y随x的增大而减小时，求k的取值范围．(本小题6.0分)如图，在△ABC中，∠C=90°，BC=5，以AB为一条边向三角形外部作正方形，已知正方形的面积是45，求△ABC的周长．(本小题7.0分)图1是某品牌婴儿车，图2为其简化结构示意图．根据安全标准需满足BC⊥CD，现测得AB=CD=6dm，BC=3dm，AD=9dm，其中AB与BD之间由一个固定为90°的零件连接(即∠ABD=90°)，通过计算说明该车是否符合安全标准．(本小题7.0分)为加强道路安全，今年年初西安市对多条道路防护栏进行维修，如图所示的是道路护栏及其简易结构图，护栏由两端立柱和中间栅栏组成，已知立柱宽度为0.1米，当立柱数目为5根时，护栏总长度为12.5米，若护栏总长度y(米)与立柱数目x(根)满足一次函数关系，写出y与x的函数关系，并求立柱数目为10根时，护栏的总长度．(本小题8.0分)阅读下面的文字，并完成相应的任务．任务：(1)若点A(-1,2)，B(1,3)，则A，B两点间的距离为______．(2)若点A(-6,-1)，点B在y轴上，且A，B两点间的距离是10，求B点的坐标．(本小题8.0分)甲、乙两汽车从A地出发，沿同一路线驶向B地．甲车先出发匀速驶向B地，0.5h后乙出发，匀速行驶一段时间后，在途中出现了故障，排除故障用了一个小时，排除故障后，为了行驶安全，速度减少了5km/h，结果与甲车同时到达B地，甲、乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示．(1)求甲汽车的速度以及点M的坐标．(2)求乙车排除故障后再次出发时，距A地的路程y与x之间的函数关系式．(3)当x=5时，甲、乙两汽车相距______km．(本小题10.0分)问题情境：老师在黑板上出了这样一道题：直线l同旁有两个定点A，B，在直线l上是否存在点P，使得PA+PB的值最小？小明的解法如下：如图1，作点A关于直线l的对称点A'，连接A'B，则A'B与直线l的交点即为P，且PA+PB的最小值为A'B．问题提出：(1)如图2，等腰Rt△ABC的直角边长为4，E是斜边AB的中点，P是AC边上的一动点，求PB+PE的最小值．问题解决：(2)如图3，为了解决A，B两村的村民饮用水问题，A，B两村计划在一水渠上建造一个蓄水池M，从蓄水池M处向A，B两村引水，A，B两村到河边的距离分别为AC=3千米，BD=9千米，CD=9千米．若蓄水池往两村铺设水管的工程费用为每千米15000元，请你在水渠CD上选择蓄水池M的位置，使铺设水管的费用最少，并求出最少的铺设水管的费用．答案和解析1.【答案】B 【解析】解：A.0.3是有限小数，属于有理数，故本选项不符合题意；B.2是无理数，故本选项符合题意；C.23是分数，属于有理数，故本选项不符合题意；D.1是整数，属于有理数，故本选项不符合题意．故选：B．根据无理数的定义判断即可．本题考查了无理数，掌握无限不循环小数是无理数是解题的关键．2.【答案】D 【解析】解：A.(-3,-2)在第三象限，故本选项不合题意；B.(2,3)在第一象限，故本选项不合题意；C.(3,-2)在第四象限，故本选项不合题意；D.(-2,4)在第二象限，故本选项符合题意；故选：D．根据第二象限内，点的横坐标小于零，纵坐标大于零，可得答案．本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限(+,+)；第二象限(-,+)；第三象限(-,-)；第四象限(+,-)．3.【答案】B 【解析】解：以2，3为直角边的直角三角形斜边长=22+32=13，故选：B．根据勾股定理可直接求解．本题考查了勾股定理，熟练掌握勾股定理是解题的关键．4.【答案】C 【解析】解：∵点M(2a,-1)与点N(4,-b)关于x轴对称，∴2a=4，-b=1，解得a=2，b=-1，则a+b=2-1=1．故选：C．直接利用关于x轴对称点的性质(横坐标不变，纵坐标互为相反数)得出a，b的值，进而得出答案．此题主要考查了关于x轴对称点的性质，正确掌握对称点坐标特点是解题关键．5.【答案】A 【解析】解：由勾股定理得，AB=42+32=5，故选：A．根据勾股定理即可求解．本题考查了勾股定理，熟练掌握勾股定理是解题的关键．6.【答案】D 【解析】解：根据平移的规则可知：将直线y=3x-1向下平移5个单位长度后所得直线的解析式为：y=3x-6，令y=0，则3x-6=0，解得x=2，∴所得直线与x轴的交点坐标为(2,0)，故选：D．根据函数的平移规则“上加下减”，即可得出直线平移后的直线解析式，再让y=0，得到关于x的方程，解方程即可求得．本题考查了一次函数图象与几何变换，解题的关键是熟记函数平移的规则“上加下减”.本题属于基础题，难度不大，解决该题型题目时，根据平移的规则求出平移后的函数解析式是关键．7.【答案】C 【解析】解：∵5≈2.236，∴5+1≈3.236，故选：C．根据5≈2.236，可得答案．本题考查了估算无理数的大小，利用5≈2.236是解题关键．8.【答案】B 【解析】解：∵直线l：y=12x+m交y轴于点B(0,1)， ∴1=12×0+m，∴直线l的解析式为y=12x+1．当y=0时，12x+1=0，解得：x=-2，∴点A的坐标为(-2,0)；当y=2时，12n+1=2，解得：n=2，∴点P的坐标为(2,2)．分两种情况考虑：①当∠AMP=90°时，PM⊥x轴，∴点M的坐标为(2,0)；②当∠APM=90°时，设点M的坐标为(a,0)，∴AP2=[2-(-2)]2+(2-0)2=20，AM2=[a-(-2)]2=a2+4a+4，PM2=(2-a)2+(2-0)2=a2-4a+8，∵AP2+PM2=AM2，∴20+a2-4a+8=a2+4a+4，解得：a=3，∴点M的坐标为(3,0)．综上所述，点M的坐标为(2,0)或(3,0)．故选：B．利用一次函数图象上点的坐标特征，可求出直线l的解析式及点A，P的坐标，分∠AMP=90°及∠APM=90°两种情况考虑：①当∠AMP=90°时，PM⊥x轴，结合点P的坐标可得出点M的坐标；②当∠APM=90°时，设点M的坐标为(a,0)，利用勾股定理，可求出a的值，进而可得出点M的坐标．本题考查了一次函数图象上点的坐标特征、直角三角形的性质以及勾股定理，分∠AMP=90°及∠APM=90°两种情况，求出点M的坐标是解题的关键．9.【答案】233 【解析】【分析】此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．直接利用二次根式的性质化简求出答案．【解答】解：43=43=233．  10.【答案】< 【解析】解：∵k=-1<0，∴y随x的增大而减小，又∵(0,y1)，(-2,y2)为直线y=-x-5上的两个点，且0>-2，∴y1-2，可得出y10，y随x的增大而增大；k<0，y随x的增大而减小”是解题的关键．11.【答案】-2 【解析】解：∵点(3m-6,4+2m)在x轴上，∴4+2m=0，解得：m=-2．故答案为：-2．直接利用x轴上点的坐标特点(纵坐标为0)得出m的值．此题主要考查了点的坐标，正确掌握点的坐标特点是解题关键．12.【答案】72 【解析】解：∵点A(-2,m)在一次函数y=2x-3的图象上，∴m=2×(-2)-3=-7，∴点A的坐标为(-2,-7)．又∵点A(-2,-7)在正比例函数y=kx的图象上，∴-7=-2k，解得：k=72，∴k的值为72．故答案为：72．利用一次函数图象上点的坐标特征，可求出m的值，进而可得出点A的坐标，再利用一次函数图象上点的坐标特征，可得出关于k的一元一次方程，解之即可得出k的值．本题考查了一次函数图象上点的坐标特征，牢记“直线上任意一点的坐标都满足函数关系式y=kx+b”是解题的关键．13.【答案】4103 【解析】解：∵∠ACB=90°，AC=3，BC=4，∴AB=AC2+BC2=32+42=5，由折叠得A'B=AB=5，∵点A的对应点A'落在BC的延长线上，∴∠A'CD=180°-∠ACB=90°，A'D=AD=3-CD，∴A'C=A'B-BC=5-4=1，∵A'C2+CD2=A'D2，∴12+CD2=(3-CD)2，∴CD=43，∴BD=BC2+CD2=42+(43)2=4103，故答案为：4103．由∠ACB=90°，AC=3，BC=4，根据勾股定理求得AB=5，由点A的对应点A'落在BC的延长线上，得∠A'CD=180°-∠ACB=90°，A'D=AD=3-CD，则A'C=A'B-BC=1，再根据勾股定理得12+CD2=(3-CD)2，求得CD=43，即可根据勾股定理求得BD=4103，于是得到问题的答案．此题重点考查轴对称的性质、勾股定理的应用等知识，在Rt△A'CD中根据勾股定理列方程是解题的关键．14.【答案】解：原式=32×6-3×33-33 =63-3-33 =23． 【解析】先化简二次根式，再计算乘法，最后计算加减即可．本题主要考查二次根式的混合运算，解题的关键是掌握二次根式的混合运算顺序和运算法则．15.【答案】解：2x2-8=0，2x2=8，x2=4，x=±2． 【解析】根据平方根的定义即可求解．本题主要考查了平方根，掌握平方根的定义是解题的关键．16.【答案】解：∵直线PQ//x轴，∴a+3=-3，解得a=-6，∴-3a-5=13，∴点P的坐标为(13,-3)． 【解析】根据直线PQ//x轴，可得a+3=-3，求出a的值，进一步可得点P坐标．本题考查了坐标与图形性质，熟练掌握平面直角坐标系内平行于x轴的直线上点的坐标特征是解题的关键．17.【答案】解：如图所示，直线l即为所求． 【解析】如果两个图形成轴对称，我们只要找到一对对应点，作出连接它们的线段的垂直平分线，就可以得到这两个图形的对称轴．本题主要考查了利用轴对称变换作图，如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．18.【答案】解：∵2a+4的立方根是2，7-b的算术平方根是3，∴2a+4=8，7-b=9，解得a=2，b=-2，∴a-b=2-(-2)=4． 【解析】根据立方根和算术平方根的定义先确定2a+4=8，7-b=9，然后解出a和b的值，再求代数式的值即可．本题考查了立方根和平方根的定义以及性质，平方根和立方根的性质：1.平方根的性质：正数a有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．2.立方根的性质：一个数的立方根只有一个，正数的立方根是正数，负数的立方根是负数，0的立方根是0．19.【答案】解：(1)当x=0时，y=2×0-4=-4， ∴一次函数y=2x-4的图象与y轴交于点(0,-4)；当y=0时，2x-4=0，解得：x=2，∴一次函数y=2x-4的图象与x轴交于点(2,0)．描点、连线，画出的直线即为一次函数y=2x-4的图象．(2)由(1)可知，点A的坐标为(2,0)，点B的坐标为(0,-4)，∴OA=2，OB=4，∴S△OAB=12OA⋅OB=12×2×4=4． 【解析】(1)利用一次函数图象上点的坐标特征，可求出一次函数图象与两坐标轴的交点坐标，描点、连线，即可画出一次函数的图象；(2)由(1)可得出点A，B的坐标，进而可得出OA，OB的长，再利用三角形的面积计算公式，即可求出S△OAB的值．本题考查了一次函数图象上点的坐标特征、一次函数的图象以及三角形的面积，解题的关键是：(1)利用一次函数图象上点的坐标特征，求出函数图象与两坐标轴的交点坐标；(2)利用三角形的面积计算公式，求出S△OAB的值．20.【答案】3 【解析】解：(1)把(0,0)代入y=(k+3)x+k2-9，得k2-9=0．解得k=3或k=-3．又因为函数y=(k+3)x+k2-9是y关于x的一次函数，所以k+3≠0，即k≠-3．所以k=3符合题意．故答案为：3；(2)根据题意，得k+3<0．解得k<-3．(1)把原点坐标代入解析式得到关于k的方程，然后解方程求出k，再利用一次函数的定义确定满足条件的k的值；(2)当y随x的增大而减小时，k+3<0.通过解该不等式即可求得答案．本题考查了一次函数图象与系数的关系，一次函数图象上点的坐标特征：一次函数图象上点的坐标满足其解析式，于是解决此类问题时把已知点的坐标代入解析式求解．注意一次项系数不为零．21.【答案】解：∵正方形的面积为45，∴AB=35，在△ABC中，∠C=90°，BC=5，∴AC=AB2-BC2=(35)2-(5)2=210．∴△ABC的周长为210+35+5=45+210． 【解析】由正方形的面积可求解AB的长，再利用勾股定理可求解AC的长，然后利用周长公式可计算三角形的周长．本题主要考查勾股定理，正方形的性质，掌握勾股定理是解题的关键．22.【答案】解：在Rt△ABD中，BD2=AD2-AB2=92-62=45，在△BCD中，BC2+CD2=32+62=45，∴BC2+CD2=BD2，∴∠BCD=90°，∴BC⊥CD．故该车符合安全标准． 【解析】在Rt△ABD中，由勾股定理求出BD，在△BCD中，通过计算，根据勾股定理逆定理判断即可．本题主要考查了勾股定理和勾股定理逆定理，熟练掌握勾股定理逆定理的应用是解决问题的关键．23.【答案】解：∵当立柱数目为5根时，护栏总长度为12.5米，∴1个栅栏的长度为12.5-0.1×55-1=3(米)，∴y=3(x-1)+0.1x=3.1x-3，即y与x的函数关系是y=3.1x-3；当x=10时，y=3.1×10-3=28(米)，答：y与x的函数关系是y=3.1x-3，立柱数目为10根时，护栏的总长度为28米． 【解析】根据立柱数目为5根时，护栏总长度为12.5米，可求出1个栅栏的长度为3米，即可得到立柱为x根时总长度y，再将x=10代入可得立柱数目为10根时，护栏的总长度．本题考查的是一次函数解决实际问题的运用，解题的关键是读懂题意，求出函数的解析式．24.【答案】5 【解析】解：(1)根据题意可得，AB=(-1-1)2+(2-3)2=4+1=5，∴A，B两点间的距离为5．故答案为：5；(2)设点B的坐标为(0,a)，根据题意可得，AB=(-6-0)2+(-1-a)2=10，∴36+(a+1)2=100，解得：a=7或a=-9，∴B点的坐标为(0,7)或(0,-9)．(1)根据两点间的距离公式，代入求值即可；(2)可设点B的坐标为(0,a)，代入两点间的距离公式，求出a的值，即可求出B点的坐标．本题考查了两点间的距离公式以及点的坐标，熟读阅读材料并能应用，结合求平方根知识点求值是解本题的关键，综合性较强，难度适中．25.【答案】15 【解析】解：(1)甲的速度为3906+0.5=60(km/h)，乙出发时，甲行驶的路程(离A地距离)为60×0.5=30(km)，∴点M的坐标为(0,30)；(2)设乙开始的速度为v千米/小时，则3v+(6-4)(v-5)=390，解得v=80(千米/小时)，∴3v=240，∴P(4,240)，设乙车排除故障后再次出发时，距A地的路程y与x之间的函数关系式为y=kx+b，把(4,240)，(6,390)代入得：4k+b=2406k+b=390，解得k=75b=-60，∴乙车排除故障后再次出发时，距A地的路程y与x之间的函数关系式为y=75x-60(4≤x≤6)；(3)当x=5时，甲车距A地(5+0.5)×60=330(km)，乙车距A地75×5-60=315(km)，∴甲、乙两汽车相距330-315=15(km)，故答案为：15．(1)用路程除以时间可得甲的速度，根据“0.5h后乙出发”可得乙出发时甲距A地的距离，从而可得M的坐标；(2)设乙开始的速度为v千米/小时，列方程算出V的值，即可得P的坐标，用待定系数法可得y与x之间的函数关系式；(3)算出x=5时，甲，乙与A地的距离，即可得到答案．本题考查一次函数的应用，解题的关键是读懂题意，数形结合解决问题．26.【答案】(1)解：如图2所示，作点B关于AC的对称点B'，连接B'E交AC于P，此时PB+PE的值最小．连接AB'． AB'=AB=AC2+BC2=42+42=42，AE=12AB=22，∵∠B'AC=∠BAC=45°，∴∠B'AB=90°，∴PB+PE的最小值=B'E=B'A2+AE2=(42)2+(22)2=210．(2)解：延长AC至A'，连接BA'交CD于点P， 则点P即为所求的水池位置，作A'E⊥BD交BD的延长线于点E，则四边形CA'ED为矩形，∴DE=A'C=AC=3，A'E=CD=9，∴BE=BD+DE=12，由勾股定理得，A'B=A'E2+BE2=92+122=15，则PA+PB=A'B=15，∴最省的铺设水管的费用W=15000×15=225000(元)； 【解析】(1)作点B关于AC的对称点B'，连接B'E交AC于P，此时PB+PE的值最小．连接AB'，先根据勾股定理求出AB'的长，再判断出∠B'AB=90°，根据勾股定理即可得出结论；(2)根据轴对称的性质确定水厂位置，作A'E⊥BD交BD的延长线于点E，根据矩形的性质分别求出DE、A'E，根据勾股定理求出A'B，得到PA+PB，结合题意计算即可．本题考查的是三角形综合题，轴对称-最短路径问题、勾股定理的应用，掌握轴对称的概念和性质、两点之间，线段最短的性质是解题的关键．两点间的距离公式如果平面直角坐标系内有两点A(x1,y1)，B(x2,y2)，那么两点的距离AB=(x1-x2)2+(y1-y2)2，则AB2=(x1-x2)2+(y1-y2)2．例如：若点A(4,1)，B(3,2)，则AB=(4-3)2+(1-2)2=2．若点A(a,1)，B(3,2)，且AB=2，则(2)2=(a-3)2+(1-2)2．