2022-2023学年浙江省丽水市青田县八校联考八年级（上）期中数学试卷(解析版)

这是一份2022-2023学年浙江省丽水市青田县八校联考八年级（上）期中数学试卷(解析版)，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年浙江省丽水市青田县八校联考八年级（上）期中数学试卷
一、选择题（本题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）
1．（3分）已知三角形的两边长分别是5cm和10cm，则下列长度的线段中能作为第三边的是（　　）
A．4cm B．5cm C．10cm D．15cm
2．（3分）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（　　）
A． B．
C． D．
3．（3分）下列语句是命题的是（　　）
A．作直线AB的垂线 B．在线段AB上取点C
C．垂线段最短吗？ D．同旁内角互补
4．（3分）如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（　　）

A．两点之间的线段最短
B．三角形具有稳定性
C．长方形是轴对称图形
D．长方形的四个角都是直角
5．（3分）用直尺和圆规作一个角等于已知角的作图痕迹如图所示，则作图的依据是（　　）

A．SSS B．SAS C．ASA D．AAS
6．（3分）适合下列条件的△ABC中，直角三角形的个数为（　　）
①∠A：∠B：∠C＝1：2：3；②∠A+∠B＝∠C；③∠A＝90°﹣∠B；④∠A＝∠B＝2∠C．
A．1 B．2 C．3 D．4
7．（3分）如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a，较短直角边长为b，大正方形面积为S1，小正方形面积为S2，则（a+b）2可表示为（　　）

A．S1﹣S2 B．2S1﹣S2 C．S1+S2 D．S1+2S2
8．（3分）如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是线段AD上的动点，E是AC边上一点．若AE＝2，当EF+CF取得最小值时，∠ECF的度数为（　　）

A．30° B．45° C．25° D．20°
9．（3分）如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且△ABC的面积是4，则△BEF的面积等于（　　）

A．0.75 B．1.25 C．2 D．1
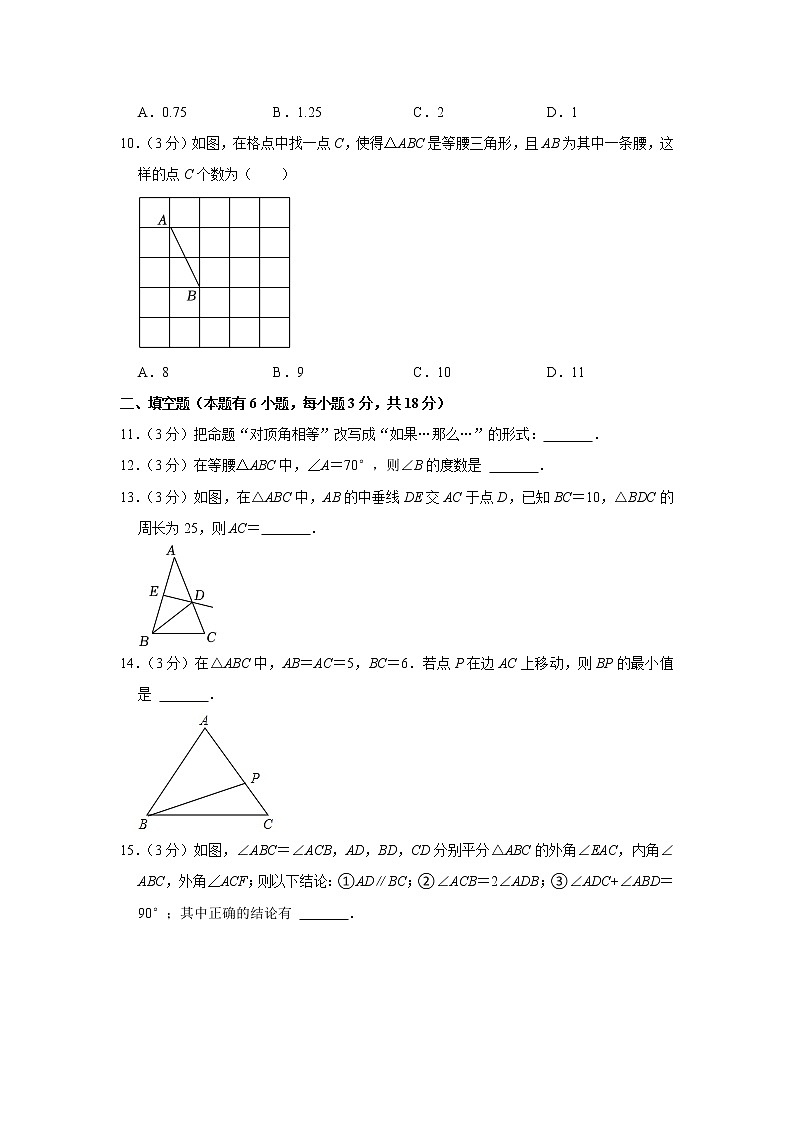
10．（3分）如图，在格点中找一点C，使得△ABC是等腰三角形，且AB为其中一条腰，这样的点C个数为（　　）

A．8 B．9 C．10 D．11
二、填空题（本题有6小题，每小题3分，共18分）
11．（3分）把命题“对顶角相等”改写成“如果…那么…”的形式：　 　．
12．（3分）在等腰△ABC中，∠A＝70°，则∠B的度数是 　 　．
13．（3分）如图，在△ABC中，AB的中垂线DE交AC于点D，已知BC＝10，△BDC的周长为25，则AC＝　 　．

14．（3分）在△ABC中，AB＝AC＝5，BC＝6．若点P在边AC上移动，则BP的最小值是 　 　．

15．（3分）如图，∠ABC＝∠ACB，AD，BD，CD分别平分△ABC的外角∠EAC，内角∠ABC，外角∠ACF；则以下结论：①AD∥BC；②∠ACB＝2∠ADB；③∠ADC+∠ABD＝90°；其中正确的结论有 　 　．

16．（3分）如图，在△ABC中，AB＝10，AC＝6，则BC边上的中线AD的取值范围是　 　．

三、解答题（本题有8小题，第17、18题5分，19～21题6分，22题7分，23题8分，24题9分，共52分，各小题都必须写出解答过程）
17．（5分）如图，在△ABC中，∠BAC＝100°，AD⊥BC于D点，AE平分∠BAC交BC于点E．若∠C＝25°，求∠DAE的度数．

18．（5分）如图，点B，F，C，E在同一条直线上，点A，D在直线BC的异侧，AB＝DE，AC＝DF，BF＝EC．
（1）求证：△ABC≌△DEF；
（2）若∠BFD＝130°，求∠ACB的度数．

19．（6分）如图，在△ABC中，点E在AB边上，请用直尺和圆规求作一点F，使得FE＝FA，且F点到AB和BC的距离相等．（保留作图痕迹，不写作法）

20．（6分）如图，已知P点是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D．
（1）求证：∠PCD＝∠PDC；
（2）求证：OP垂直平线段CD．

21．（6分）如图，已知在Rt△ABC中，∠ACB＝90°，AC＝9，BC＝12，AB的垂直平分线交AB于点D，交BC于点E，连结AE，求BE的长．

22．（7分）如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，AD与BE交于点F，AD＝BD，
求证：（1）△ACD≌△BFD；
（2）BF＝2AE．

23．（8分）如图，已知等腰△ABC中，AB＝AC，∠A＜90°，CD是△ABC的高，BE是∠ABC的角平分线，CD与BE交于点P．
（1）当∠A＝52°时，求∠BPC的度数；
（2）当∠A＝x°时，求∠BPC的度数（请用含x的代数式表示），并说明理由．

24．（9分）已知△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，F为BE的中点，连结DF，CF．
（1）如图①，当点D在AB上，点E在AC上，请写出此时线段DF，CF的数量关系和位置关系，并说明理由．
（2）如图②，在（1）的条件下将△ADE绕点A顺时针旋转45°，请你判断此时（1）中的结论是否仍然成立，并证明你的判断．


2022-2023学年浙江省丽水市青田县八校联考八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本题有10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）
1．（3分）已知三角形的两边长分别是5cm和10cm，则下列长度的线段中能作为第三边的是（　　）
A．4cm B．5cm C．10cm D．15cm
【分析】设三角形第三边的长为x，再根据三角形的三边关系求出x的取值范围，找出不符合条件的x的值即可．
【解答】解：设三角形第三边的长为xcm，
∵三角形的两边长分别是5cm和10cm，
∴10cm﹣5cm＜x＜10cm+5cm，即5cm＜x＜15cm，
∴四个选项中只有C符合．
故选：C．
2．（3分）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（　　）
A． B．
C． D．
【分析】根据三角形高线的定义：过三角形的顶点向对边引垂线，顶点和垂足之间的线段叫做三角形的高线解答．
【解答】解：为△ABC中BC边上的高的是A选项．
故选：A．
3．（3分）下列语句是命题的是（　　）
A．作直线AB的垂线 B．在线段AB上取点C
C．垂线段最短吗？ D．同旁内角互补
【分析】利用命题的定义分别判断后即可确定正确的选项．
【解答】解：A．作直线AB的垂线为描述性语言，它不是命题，所以A选项不符合题意；
B．在线段AB上取点C为描述性语言，它不是命题，所以B选项不符合题意；
C．垂线段最短吗为疑问句，它不是命题，所以C选项不符合题意；
D．同旁内角互补为命题，所以D选项符合题意．
故选：D．
4．（3分）如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（　　）

A．两点之间的线段最短
B．三角形具有稳定性
C．长方形是轴对称图形
D．长方形的四个角都是直角
【分析】根据三角形的稳定性，可直接得出结论．
【解答】解：加上EF后，原图形中具有△AEF了，故这种做法根据的是三角形的稳定性．
故选：B．
5．（3分）用直尺和圆规作一个角等于已知角的作图痕迹如图所示，则作图的依据是（　　）

A．SSS B．SAS C．ASA D．AAS
【分析】由作法可知，两三角形的三条边对应相等，所以利用SSS可证得△OCD≌△O′C′D′，那么∠A′O′B′＝∠AOB．
【解答】解：由作法易得OD＝O′D'，OC＝0′C'，CD＝C′D'，那么△OCD≌△O′C′D′，可得∠A′O′B′＝∠AOB，所以利用的条件为SSS．
故选：A．
6．（3分）适合下列条件的△ABC中，直角三角形的个数为（　　）
①∠A：∠B：∠C＝1：2：3；②∠A+∠B＝∠C；③∠A＝90°﹣∠B；④∠A＝∠B＝2∠C．
A．1 B．2 C．3 D．4
【分析】先根据三角形的内角和是180°对①②③④中△ABC的形状作出判断即可．
【解答】解：①∵∠A：∠B：∠C＝1：2：3，
∴设∠A＝x，则∠B＝2x，∠C＝3x，
∴x+2x+3x＝180°，解得x＝30°，
∴∠C＝3x＝90°，
∴△ABC是直角三角形，故本小题正确；
②∵∠A+∠B＝∠C，
∴2∠C＝180°，解得∠C＝90°，故本小题正确；
③∵∠A＝90°﹣∠B，
∴∠A+∠B＝90°，
∴∠C＝180°﹣90°＝90°，故本小题正确；
④∵∠A＝∠B＝2∠C，
∴5∠C＝180°，解得∠C＝36°，
∴∠A＝∠B＝72°，故本小题错误．
故选：C．
7．（3分）如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a，较短直角边长为b，大正方形面积为S1，小正方形面积为S2，则（a+b）2可表示为（　　）

A．S1﹣S2 B．2S1﹣S2 C．S1+S2 D．S1+2S2
【分析】根据图形和勾股定理可知S1＝c2＝a2+b2，再由完全平方公式即可得到结果．
【解答】解：如图所示：设直角三角形的斜边为c，
则S1＝c2＝a2+b2，
S2＝（a﹣b）2＝a2+b2﹣2ab，
∴2ab＝S1﹣S2，
∴（a+b）2＝a2+2ab+b2＝S1+S1﹣S2＝2S1﹣S2，
故选：B．

8．（3分）如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是线段AD上的动点，E是AC边上一点．若AE＝2，当EF+CF取得最小值时，∠ECF的度数为（　　）

A．30° B．45° C．25° D．20°
【分析】过E作EM∥BC，交AD于N，连接CM交AD于F，连接EF，推出M为AB中点，求出E和M关于AD对称，根据等边三角形性质求出∠ACM，即可求出答案．
【解答】解：过E作EM∥BC，交AD于N，

∵AC＝4，AE＝2，
∴EC＝2＝AE，
∴AM＝BM＝2，
∴AM＝AE，
∵AD是BC边上的中线，△ABC是等边三角形，
∴AD⊥BC，
∵EM∥BC，
∴AD⊥EM，
∵AM＝AE，
∴E和M关于AD对称，
连接CM交AD于F，连接EF，
则此时，EF+CF的值最小，
∵△ABC是等边三角形，
∴∠ACB＝60°，AC＝BC，
∵AM＝BM，
∴∠ECF＝∠ACB＝30°，
故选：A．
9．（3分）如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且△ABC的面积是4，则△BEF的面积等于（　　）

A．0.75 B．1.25 C．2 D．1
【分析】根据点D是BC的中点，可得△ABD的面积＝△ADC的面积＝2，再根据点E是AD的中点，可得△BDE的面积＝1，△CDE的面积＝1，从而可得△BEC的面积＝2，然后根据点F是CE的中点，可得△BEF的面积＝△BEC的面积＝1，即可解答．
【解答】解：∵点D是BC的中点，△ABC的面积是4，
∴△ABD的面积＝△ADC的面积＝△ABC的面积＝×4＝2，
∵点E是AD的中点，
∴△BDE的面积＝△ABD的面积＝×2＝1，△CDE的面积＝△ADC的面积＝×2＝1，
∴△BEC的面积＝△BED的面积+△CDE的面积＝2，
∵点F是CE的中点，
∴△BEF的面积＝△BEC的面积＝×2＝1，
故选：D．
10．（3分）如图，在格点中找一点C，使得△ABC是等腰三角形，且AB为其中一条腰，这样的点C个数为（　　）

A．8 B．9 C．10 D．11
【分析】根据等腰三角形的判定，分情况讨论：AB＝AC，AB＝BC即可确定点C的个数．
【解答】解：如图所示：

满足条件的点C有9个，
故选：B．
二、填空题（本题有6小题，每小题3分，共18分）
11．（3分）把命题“对顶角相等”改写成“如果…那么…”的形式：　如果两个角是对顶角，那么这两个角相等　．
【分析】命题中的条件是两个角是对顶角，放在“如果”的后面，结论是这两个角相等，应放在“那么”的后面．
【解答】解：题设为：两个角是对顶角，结论为：这两个角相等，
故写成“如果…那么…”的形式是：如果两个角是对顶角，那么这两个角相等，
故答案为：如果两个角是对顶角，那么这两个角相等．
12．（3分）在等腰△ABC中，∠A＝70°，则∠B的度数是 　55°或40°或70°　．
【分析】∠A为顶角、∠B为顶角和∠A、∠B为底角，再根据三角形内角和定理可求得∠B的度数．
【解答】解：当∠A为顶角时，则∠B＝＝55°；
当∠B为顶角时，则∠B＝180°﹣2∠A＝40°；
当∠A、∠B为底角时，则∠B＝∠A＝70°；
故答案为：55°或40°或70°．
13．（3分）如图，在△ABC中，AB的中垂线DE交AC于点D，已知BC＝10，△BDC的周长为25，则AC＝　15　．

【分析】利用线段垂直平分线的性质可得DB＝DA，然后根据已知△BDC的周长为25，可得BC+CA＝25，最后进行计算即可解答．
【解答】解：∵DE是AB的中垂线，
∴DB＝DA，
∵△BDC的周长为25，
∴BC+BD+CD＝25，
∴BC+CD+DA＝25，
∴BC+CA＝25，
∵BC＝10，
∴AC＝25﹣10＝15．
故答案为：15．
14．（3分）在△ABC中，AB＝AC＝5，BC＝6．若点P在边AC上移动，则BP的最小值是 　4.8　．

【分析】根据点与直线上各点的连线中，垂线段最短，得到当BP垂直于AC时，BP的长最小，过A作等腰三角形底边上的高AD，利用三线合一得到D为BC的中点，在直角三角形ADC中，利用勾股定理求出AD的长，进而利用面积法即可求出此时BP的长．
【解答】解：根据垂线段最短，得到BP⊥AC时，BP最短，
过A作AD⊥BC，交BC于点D，
∵AB＝AC，AD⊥BC，
∴D为BC的中点，又BC＝6，
∴BD＝CD＝3，
在Rt△ADC中，AC＝5，CD＝3，
根据勾股定理得：AD＝＝4，
又∵S△ABC＝BC•AD＝BP•AC，
∴BP＝＝＝4.8．
故答案为：4.8．

15．（3分）如图，∠ABC＝∠ACB，AD，BD，CD分别平分△ABC的外角∠EAC，内角∠ABC，外角∠ACF；则以下结论：①AD∥BC；②∠ACB＝2∠ADB；③∠ADC+∠ABD＝90°；其中正确的结论有 　①②③　．

【分析】根据角平分线定义得出∠ABC＝2∠ABD＝2∠DBC，∠EAC＝2∠EAD，∠ACF＝2∠DCF，根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB＝180°，根据三角形外角性质得出∠ACF＝∠ABC+∠BAC，∠EAC＝∠ABC+∠ACB，根据已知结论逐步推理，即可判断各项．
【解答】解：∵AD平分∠EAC，
∴∠EAC＝2∠EAD，
∵∠EAC＝∠ABC+∠ACB，∠ABC＝∠ACB，
∴∠EAD＝∠ABC，
∴AD∥BC，
∴①正确；
∵AD∥BC，
∴∠ADB＝∠DBC，
∵BD平分∠ABC，∠ABC＝∠ACB，
∴∠ABC＝∠ACB＝2∠DBC，
∴∠ACB＝2∠ADB，
∴②正确；
∵AD∥BC，
∴∠ADC＝∠DCF，
∵CD平分∠ACF，
∴∠ACF＝2∠DCF，
∵ACB+CACF＝180°，∠ACB＝∠ABC＝2∠ABD，
∴2∠ABD+2∠ADC＝180°，
∴∠ABD+∠ADC＝90°，故③正确；
故答案为：①②③．
16．（3分）如图，在△ABC中，AB＝10，AC＝6，则BC边上的中线AD的取值范围是　2＜AD＜8　．

【分析】延长AD至E，使DE＝AD，由SAS证明△ACD≌△EBD，得出BE＝AC＝6，在△ABE中，由三角形的三边关系求出AE的取值范围，即可得出AD的取值范围；
【解答】（1）解：延长AD至E，使DE＝AD，连接BE，如图1所示
∵AD是BC边上的中线，
∴BD＝CD，
在△BDE和△CDA中，
，
∴△BDE≌△CDA（SAS），
∴BE＝AC＝6，
在△ABE中，由三角形的三边关系得：AB﹣BE＜AE＜AB+BE，
∴10﹣6＜AE＜10+6，即4＜AE＜16，
∴2＜AD＜8；
故答案为2＜AD＜8．

三、解答题（本题有8小题，第17、18题5分，19～21题6分，22题7分，23题8分，24题9分，共52分，各小题都必须写出解答过程）
17．（5分）如图，在△ABC中，∠BAC＝100°，AD⊥BC于D点，AE平分∠BAC交BC于点E．若∠C＝25°，求∠DAE的度数．

【分析】先根据角平分线的定义求得∠EAC的度数，再由外角的性质得∠AED，最后由直角三角形的性质可得结论．
【解答】解：∵AE平分∠BAC，
∴∠EAC＝＝＝50°，
∵∠C＝25°，
∴∠AED＝∠C+∠EAC＝25°+50°＝75°，
∵AD⊥BC，
∴∠ADE＝90°，
∴∠DAE＝90°﹣75°＝15°．
18．（5分）如图，点B，F，C，E在同一条直线上，点A，D在直线BC的异侧，AB＝DE，AC＝DF，BF＝EC．
（1）求证：△ABC≌△DEF；
（2）若∠BFD＝130°，求∠ACB的度数．

【分析】（1）根据BF＝EC，可以得到BC＝EF，然后根据题目中的条件，利用全等三角形的判定即可证明结论成立；
（2）根据邻补角互补和全等三角形的性质可以得到∠ACB的度数．
【解答】（1）证明：∵BF＝EC，
∴BF+FC＝EC+FC，
∴BC＝EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS）；
（2）∵∠BFD＝130°，∠BFD+∠DFE＝180°，
∴∠DFE＝50°，
由（1）知，△ABC≌△DEF，
∴∠ACB＝∠DFE，
∴∠ACB＝50°．
19．（6分）如图，在△ABC中，点E在AB边上，请用直尺和圆规求作一点F，使得FE＝FA，且F点到AB和BC的距离相等．（保留作图痕迹，不写作法）

【分析】作AE的垂直平分线和∠ABC的角平分线，它们的交点即为F点．
【解答】解：如图，点F为所作．

20．（6分）如图，已知P点是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D．
（1）求证：∠PCD＝∠PDC；
（2）求证：OP垂直平线段CD．

【分析】（1）由角平分线的性质可得PC＝PD，可得结论；
（2）由“HL”可证Rt△POC≌Rt△POD，可得OC＝OD，可得结论．
【解答】证明：（1）∵OP是∠AOB的平分线，PC⊥OA，PD⊥OB，
∴PC＝PD，
∴∠PCD＝∠PDC；
（2）∵PC⊥OA，PD⊥OB，
∴∠OCP＝∠ODP＝90°，
在Rt△POC和Rt△POD中，
，
∴Rt△POC≌Rt△POD（HL），
∴OC＝OD，
∵PC＝PD，OC＝OD，
∴OP垂直平线段CD．
21．（6分）如图，已知在Rt△ABC中，∠ACB＝90°，AC＝9，BC＝12，AB的垂直平分线交AB于点D，交BC于点E，连结AE，求BE的长．

【分析】由勾股定理得出AB的长，再由线段垂直平分线的性质得出AE＝BE，设BE＝AE＝x，则CE＝12﹣x，再根据勾股定理得出方程求解即可．
【解答】解：在Rt△ABC中，由勾股定理得，
AB＝＝＝15，
∵DE垂直平分线AB，
∴AE＝BE，
设BE＝AE＝x，则CE＝12﹣x，
在Rt△ACE中，由勾股定理得，
AE2＝AC2+CE2，
即x2＝92+（12﹣x）2，
解得x＝，
即BE的长为．
22．（7分）如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，AD与BE交于点F，AD＝BD，
求证：（1）△ACD≌△BFD；
（2）BF＝2AE．

【分析】（1）先判定出△ABD是等腰直角三角形，根据等腰直角三角形的性质可得AD＝BD，再根据同角的余角相等求出∠CAD＝∠CBE，然后利用“角边角”证明△ACD≌△BFD即可；
（2）根据全等三角形对应边相等可得BF＝AC，再根据等腰三角形三线合一的性质可得AC＝2AE，从而得证．
【解答】（1）∵AD⊥BC，∠BAD＝45°，
∴△ABD是等腰直角三角形，
∴AD＝BD，
∵BE⊥AC，AD⊥BC，
∴∠CAD+∠ACD＝90°，∠CBE+∠ACD＝90°，
∴∠CAD＝∠CBE，
在△ADC和△BDF中，
，
∴△ACD≌△BFD（ASA）；
（2）证明：由（1）可知：BF＝AC，
∵AB＝BC，BE⊥AC，
∴AC＝2AE，
∴BF＝2AE．
23．（8分）如图，已知等腰△ABC中，AB＝AC，∠A＜90°，CD是△ABC的高，BE是∠ABC的角平分线，CD与BE交于点P．
（1）当∠A＝52°时，求∠BPC的度数；
（2）当∠A＝x°时，求∠BPC的度数（请用含x的代数式表示），并说明理由．

【分析】（1）利用等腰三角形的性质可得∠ABC＝∠ACB＝64°，再利用角平分线的定义可得∠ABE＝32°，然后利用垂直定义可得∠CDB＝90°，从而利用三角形外角的性质，进行计算即可解答；
（2）利用（1）的解题思路，进行计算即可解答．
【解答】解：（1）∵AB＝AC，∠A＝52°，
∴∠ABC＝∠ACB＝（180°﹣∠A）＝64°，
∵BE平分∠ABC，
∴∠ABE＝∠ABC＝32°，
∵CD⊥AB，
∴∠CDB＝90°，
∴∠BPC＝∠ABE+∠BDP＝122°，
∴∠BPC的度数为122°；
（2）∠BPC的度数为（135﹣x）°，
理由：∵AB＝AC，∠A＝x°，
∴∠ABC＝∠ACB＝（180°﹣∠A）＝（90﹣x）°，
∵BE平分∠ABC，
∴∠ABE＝∠ABC＝（45﹣x）°，
∵CD⊥AB，
∴∠CDB＝90°，
∴∠BPC＝∠ABE+∠BDP＝（135﹣x）°，
∴∠BPC的度数为（135﹣x）°．
24．（9分）已知△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，F为BE的中点，连结DF，CF．
（1）如图①，当点D在AB上，点E在AC上，请写出此时线段DF，CF的数量关系和位置关系，并说明理由．
（2）如图②，在（1）的条件下将△ADE绕点A顺时针旋转45°，请你判断此时（1）中的结论是否仍然成立，并证明你的判断．

【分析】（1）根据“直角三角形斜边上的中线等于斜边的一半”可知DF＝BF＝CF，根据∠DFE＝2∠DCF，∠BFE＝2∠BCF，得到∠EFD+∠EFB＝2∠ABC＝90°，进而得出DF⊥BF；
（2）延长DF交BC于点G，，先判定△BFG≌△EFD（AAS），得到DF＝GF，BG＝ED，结合△ADE和△ACB都是等腰直角三角形，得到DC＝GC，根据△DCG是等腰直角三角形，以及F是DG的中点，即可得到CF⊥DF且CF＝DF．
【解答】解：（1）CF＝DF且CF⊥DF．


∵∠ADE＝90°，
∴∠BDE＝90°，
又∵∠BCE＝90°，点F是BE的中点，
∴CF＝DF＝BE＝BF，
∴∠EBC＝∠FCB，∠ABE＝∠BDF，
∴∠EFC＝∠EBC+∠FCB＝2∠EBC，∠DFE＝ABE+∠BDF＝2∠ABE，
∴∠CFD＝∠EFC+∠EFD＝2（∠EBC+∠ABE）＝2∠ABC，
又∵△ABC是等腰直角三角形，且∠ACB＝90°，
∴∠ABC＝45°，
∴∠CFD＝90°，
∴CF＝DF且CF⊥DF．

（2）（1）中的结论仍然成立．理由如下：
如图：延长DF交BC于点G，


∵∠ADE＝∠ACB＝90°，
∴DE∥BC，
∴∠DEF＝∠GBF，
∠EDF＝∠BGF，
∵F是BE的中点，
∴BF＝EF，
∴△BFG≌△EFD（AAS），
∴DF＝GF，BG＝ED，
∵AD＝DE，
∴AD＝BG，
∵AC＝BC，
∴AC﹣AD＝BC﹣GB，
∴DC＝GC，
∵∠ACB＝90°，
∴△DCG是等腰直角三角形，
又∵F是DG的中点，
∴CF⊥DF且CF＝DF．