



【期末满分冲刺】人教版数学七年级上册-专项01《以数轴为背景的动点问题》期末重难点突破
展开专项1:以数轴为背景的动点问题
考点导图
素质拓展
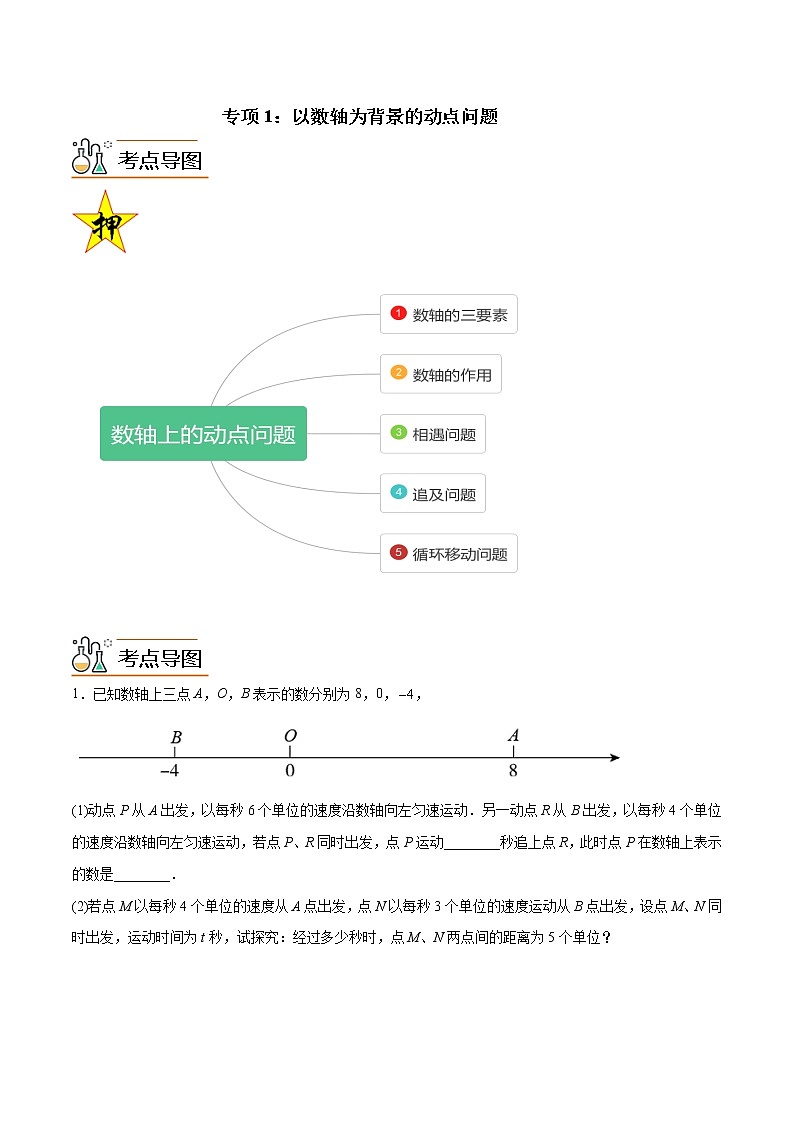
1.已知数轴上三点A,O,B表示的数分别为8,0,,
(1)动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,点P运动________秒追上点R,此时点P在数轴上表示的数是________.
(2)若点M以每秒4个单位的速度从A点出发,点N以每秒3个单位的速度运动从B点出发,设点M、N同时出发,运动时间为t秒,试探究:经过多少秒时,点M、N两点间的距离为5个单位?
【答案】(1)6,28;
(2)M,N都向左运动,经过7秒或17秒时,点M、N两点间的距离为5个单位,M向左运动,N向右运动,经过1秒或秒时,点M、N两点间的距离为5个单位.
【分析】(1)用含t的代数式表示P,R运动后表示的数,列方程可得答案;
(2)由M,N运动方向不同,分两种情况列方程,即可解得答案.
(1)
解:设点P、R运动时间是t秒,则运动后P表示的数是8-6t,R运动后表示的数是-4-4t,
根据题意得:8-6t=-4-4t,
解得t=6,
∴点P运动6秒追上点R,此时点P在数轴上表示的数是8-6×6=-28,
故答案为:6,28;
(2)
解:①M,N都向左运动,M表示的数是8-4t,N表示的数是-4-3t,
∴(8-4t)-(-4-3t)=5或(-4-3t)-(8-4t)=5,
解得t=7或t=17;
②M向左运动,N向右运动,M表示的数是8-4t,N表示的数是-4+3t,
∴(8-4t)-(-4+3t)=5或(-4+3t)-(8-4t)=5,
解得t=1或t=,
综上所述,M,N都向左运动,经过7秒或17秒时,点M、N两点间的距离为5个单位,M向左运动,N向右运动,经过1秒或秒时,点M、N两点间的距离为5个单位.
【我思故我在】本题考查一元一次方程的应用,解题的关键是能用含t的代数式表示点运动后表示的数.
2.对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.
例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A,C的“联盟点”.
(1)若点A表示数,点B表示数5,点M是点A,B的“联盟点”,点M在A、B之间,且表示一个负数,则点M表示的数为____________;
(2)若点A表示数,点B表示数2,下列各数,0,4,6所对应的点分别为,,,,其中是点A,B的“联盟点”的是____________;
(3)点A表示数,点B表示数25,P为数轴上一点:
①若点P在点B的左侧,且点P是点A,B的“联盟点”,此时点P表示的数是____________;
②若点P在点B的右侧,点P,A,B中,有一个点恰好是其它两个点的“联盟点”,直接写出此时点P表示的数____________.
【答案】(1)-1;
(2)C1或C4;
(3)①;②65;45;105.
【分析】(1)先求出AB=9,再根据联盟点的定义求出M表示的数是2与 -1,最后根据点M表示一个负数,即可求解;
(2)根据题意求得CA与BC的关系,得到答案;
(3)①分点P位于点A左侧、点P表示的数位于AB之间,且靠近点A、点P表示的数位于AB之间,且靠近点B三种情况讨论,即可求解;
②分当P为A、B的联盟点、点B为AP联盟点且AB=2BP、点B为AP联盟点且PB=2AB三种情况讨论,即可求解.
(1)
解:由题意得,因为点M是点A,B的“联盟点”,点M在A、B之间,
∴AM=2BM,或BM=2AM,
所以AM= 或AM= ,
所以点M表示的数是-4+6=2或-4+3=-1,
因为点M表示一个负数,
所以点M表示的数为-1.
故答案为:-1;
实战演练
3.[背景知识]:数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为8,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C是M、N的幸福中心,则C所表示的数是多少?
(3)如图3,点A表示的数是0,点B表示的数是4,若点A、点B同时以1个单位长度/秒的速度向左运动,与此同时点P从10处以2个单位长度/秒的速度向左运动,经过多长时间后,点A、点B、点P三点中其中一点是另外两点的幸福中心?(直接写出答案.)
【答案】(1)2或-4
(2)5或-3
(3)2s或4s或6s或10s或12s或14s
【分析】对于(1),根据幸福点的定义解答即可;
对于(2),分点C在点M的右侧,在MN之间,在点N的左侧时,根据幸福中心的定义解答即可;
对于(3),分点P在线段AB右侧,在线段上,在线段AB的左侧三种情况,结合幸福中心的定义列出方程,求出解即可.
(1)2或-4.
设点C表示的数是x,根据题意,得
,
解得或.
故答案为:2或-4;
(2)
解:设C所表示的数是x,有三种情况:
①当C在M右侧时:
CM+CN=8,
即(x-4)+(x+2)=8,
解得:x=5;
②当C在MN之间时:
CM+CN=6,
此种情况不成立;
③当C在N左侧时:
CM+CN=8,
即(4-x)+(-2-x)=8,
解得:x=-3.
综上所述,C所表示的数是5或-3;
(3)
2s或4s或6s或10s或12s或14s.
点P在线段AB的右侧;
设经过x秒点B是点A,点P的“幸福中心”,根据题意,得
,
解得x=2;
设经过x秒点P是点A,点B的“幸福中心”,根据题意,得
,
解得x=4;
点P在线段AB上,与点B或点A重合时;
设经过x秒点A是点B,点P的“幸福中心”,根据题意,得
,
解得x=6;
设经过x秒点B是点A,点P的“幸福中心”,根据题意,得
,
解得x=10;
点P在线段AB的左侧时;
设经过x秒点P是点A,点B的“幸福中心”,根据题意,得
,
解得x=12;
设经过x秒点A是点B,点P的“幸福中心”,根据题意,得
,
解得x=14;
故答案为:2s或4s或6s或10s或12s或14s.
【我思故我在】本题主要考查了动点问题在数轴上的应用,理解新定义是解题的关键,同时注意多种情况讨论.
4.如图,数轴上点A、B表示的数分别是-4和2.
(1)A、B两点间的距离为 .
(2)点P为线段AB上的一个运动点,动点P以每秒3个单位长度的速度,从点A出发沿数轴向终点B运动.当点P运动1秒时,点P表示的数为 .
(3)在(2)的条件下,点P出发的同时,动点Q以每秒1个单位长度的速度从点B出发,沿数轴向右运动,点P到达点B时,两点同时停止运动.当P、Q两点表示的数互为相反数时,点P表示的数为 .
(4)在(2)的条件下,点P出发的同时,动点Q以每秒1个单位长度的速度从点B出发,沿数轴向左运动,点P到达点B时,两点同时停止运动.当点P表示数与点Q表示数的绝对值之差为1时,直接写出点P表示的数.
【答案】(1)6
(2)-1
(3)
(4)点P表示的数是或
【分析】(1)数轴上两点之间的距离等于这两点对应的数的差的绝对值,由此求出A、B两点间的距离即可;
(2)向右运动的点表示的数等于该点原来对应的数加上运动的速度与时间的乘积,由此即可计算出运动1秒时点P表示的数;
(3)设运动t秒时,P、Q两点表示的数互为相反数,点P和点Q表示的数分别为−4+3t和2+t,可列方程−4+3t+2+t=0,解方程求出t的值,再求出点P表示的数即可;
(4)设运动的时间为t秒,则点P和点Q表示的数分别为−4+3t和2−t,由3t=4得;由3t=6得t=2,可知运动秒点P与原点重合;运动2秒点P到达终点B,此时点Q与原点重合,所以应分两种情况求t的值,一是点P在原点左侧,点Q在原点右侧,可列方程−(−4+3t)=2−t+1或−(−4+3t)+1=2−t;二是点P与点Q都在原点右侧,可列方程−4+3t=2−t+1或−4+3t+1=2−t,解方程求出符合题意的t值,再求出点P表示的数即可.
(1)
解:|−4−2|=6,
所以A、B两点间的距离是6,
故答案为:6.
(2)
解:−4+3×1=−1,
所以点P运动1秒时,点P表示的数是−1.
故答案为:−1.
(3)
解:设运动t秒时,P、Q两点表示的数互为相反数,
根据题意得:−4+3t+2+t=0,
解得:,
所以−4+3×=,
所以点P表示的数是.
(4)
解:设运动的时间为t秒,
由3t=4得;
由3t=6得t=2,
可知运动秒点P与原点重合;运动2秒点P到达终点B,此时点Q与原点重合,
当点P在原点左侧,点Q在原点右侧时,
根据题意得:−(−4+3t)=2−t+1或−(−4+3t)+1=2−t,
解得t=或t=(不符合题意,舍去);
所以−4+3×=,
即点P表示的数是;
当点P与点Q都在原点右侧时,
根据题意得−4+3t=2−t+1或−4+3t+1=2−t,
解得t=或t=(不符合题意,舍去),
所以−4+3×=,
即点P表示的数是,
综上所述,点P表示的数是或.
【我思故我在】本题主要考查解一元一次方程、列一元一次方程解应用题、数轴上两点之间的距离,数轴上的动点问题,正确地用代数式表示运动过程中的点对应的数,根据题意列出关于t的方程,是解题的关键.
5.已知在纸面上有一数轴(如图所示).
(1)操作一:折叠纸面,使表示数1的点与表示数﹣1的点重合,则此时表示数4的点与表示数 的点重合;
(2)操作二:折叠纸面,使表示数6的点与表示数﹣2的点重合,回答下列问题:
①表示数9的点与表示数 的点重合;
②若这样折叠后,数轴上的A,B两点也重合,且A,B两点之间的距离为10(点A在点B的左侧),求A,B两点所表示的数分别是多少?
③在②的条件下,在数轴上找到一点P,设点P表示的数为x.当PA+PB=12时,直接写出x的值.
【答案】(1)-4
(2)①-5;②A、B两点表示的数分别是-3,7;③x的值为-4或8.
【分析】(1)先求出中心点,再求出对应的数即可;
(2)①求出中心点是表示2的点,再根据对称求出即可;②求出中心点是表示2的点,求出A、B到表示2的点的距离是5,即可求出答案;③根据点P在数轴上的位置,分类讨论,当点P在点A的左侧时,当点P在点A、B之间时,当点P在点A的右侧时,根据各种情形求解即可.
(1)
解:∵折叠纸面,使数字1表示的点与-1表示的点重合,可确定中心点是表示0的点,
∴4表示的点与-4表示的点重合,
故答案为∶-4;
(2)
解:①∵折叠纸面,使表示数6的点与表示数﹣2的点重合,可确定中心点是表示2的点,
∴表示数9的点与表示数-5的点重合;
故答案为∶ -5;
②∵折叠后,数轴上的A,B两点也重合,且A,B两点之间的距离为10(点A在点B的左侧),
∴A、B两点距离中心点的距离为10 ÷2= 5,
∵中心点是表示2的点,
∴A、B两点表示的数分别是-3,7;
③当点P在点A的左侧时,
∵PA+PB=12,
∴-3-x+7-x=12,
解得x=-4;
当点P在点A、B之间时,此时PA+PB=12不成立,故不存在点P在点A、B之间的情形;
当点P在点A的右侧时,
∵PA+PB=12,
∴x-(-3)+x-7=12,
解得x=8,
综上x的值为-4或8.
【我思故我在】本题考查了数轴的应用,能求出折叠后的中心点的位置是解此题的关键.
6.对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足3倍的数量关系,则称该点是其它两个点的“倍分点”.如图,数轴上点A,B,C表示的数分别是1,4,5,此时点B是点A,C的“倍分点”.
(1)当点A表示数﹣2,点B表示数2时,下列各数,1,4是点A,B的“倍分点”的是 ;
(2)当点A表示数﹣10,点B表示数30时,D为数轴上一个动点.
①若点D是点A,B的“倍分点”,求此时点D表示的数;
②若点D,A,B中,有一个点恰好是其它两个点的“倍分点”,求出此时点D表示的数.
【答案】(1)1,4;
(2)①点D表示的数可为20,0,50,﹣30;②D表示的数可为:20,0,50,﹣30,,﹣130,,110,,﹣90,150,
【分析】(1)分别计算,1,4与点A,B的距离,根据定义判断即可;
(2)设点D对应的数为x,①分四种情况,当点D在A,B之间时,当BD=AB时,当BD=AB时;当点D在点B右侧,当点D在点A左侧,分别列方程求解;
②分情况:当点A、B、D分别为“倍分点”时,分别列方程计算即可.
(1)
解:∵﹣2+=0.5,2+=4.5,
∴数-不是点A,B的“倍分点”;
∵1+2=3,2﹣1=1,
∴数1是点A,B的“倍分点”;
∵4﹣(﹣2)=6,4﹣2=2,
∴数4是点A,B的“倍分点”;
故答案为:1,4;
(2)
设点D对应的数为x,
①当点D在A,B之间时,因为AB=30+10=40,
所以当BD=AB时,BD=10,即x=30﹣10=20;
当BD=AB时,BD=30,即x=30﹣30=0;
当点D在点B右侧,AD=3BD,即x+10=3(x﹣30),解得x=50;
当点D在点A左侧,BD=3AD,即30﹣x=3(﹣10﹣x),解得x=﹣30;
综上,点D表示的数可为20,0,50,﹣30;
②由①得点D是倍分点时,点D表示的数可为20,0,50,﹣30;
当点A为倍分点,点D在A,B之间时,AB=3AD,即40=3(x+10),解得x=;
点D在点A左侧时,AD=3AB,即﹣10﹣x=3×40,解得x=﹣130;
AB=3AD,即40=3(﹣10﹣x),解得x=;
点D在点B右侧,AD=3AB,即x﹣(﹣10)=3×40,解得x=110;
当点B为倍分点时,同理可求x=,﹣90,150,;
综上,点D表示的数可为:20,0,50,﹣30,,﹣130,,110,,﹣90,150,.
【我思故我在】此题考查了有理数的加减计算的应用,一元一次方程的应用,数轴上动点问题的理解,数轴上两点之间的距离,正确理解数轴上两点之间的距离是解题的关键.
7.如图,已知数轴上有A、B两点,点B在原点的右侧,到原点的距离为2,点A在点B的左侧,AB=18.动点P、Q分别从A、B两点同时出发,在数轴上匀速运动,它们的速度分别为3个单位长度/秒、1个单位长度/秒,设运动时间为t秒.
(1)点A表示的数为 ,点B表示的数为
(2)若动点P、Q均向右运动.当t=2时,点P对应的数是 ,P、Q两点间的距离为 个单位长度.请问当t为何值时,点P追上点Q,并求出此时点P对应的数;
(3)若动点Q从B点向左运动到原点后返回到B点停止,动点P从A点向右运动,当点Q停止时,点P也停止运动.请直接写出当t为何值时,在PA、PB和AB三条线段中,其中一条线段的长度是另一条线段长度的3倍.
【答案】(1)2,﹣16
(2)﹣10,14;11
(3)当t为1.5,2或4时,在PA、PB和AB三条线段中,其中一条线段的长度是另一条线段长度的3倍.
【分析】(1)利用两点间的距离,有理数在数轴上的表示可得.
(2)利用两点间的距离,有理数在数轴上的表示可得;利用行程公式建立等式求解可得.
(3)采用分类讨论,再利用两点间的距离、行程公式建立等式求解即可.
(1)
解:∵点B在原点的右侧,到原点的距离为2,
∴点B表示的数为2.
∵点A在点B的左侧,AB=18,
∴2﹣18=﹣16.
∴点A表示的数为:﹣16.
故答案为:﹣16,2.
(2)
解:当t=2时,3×2=6,1×2=2,
∴点P向右运动了6个单位长度,点Q向右运动了2个单位长度.
∴﹣16+6=﹣10,2+2=4.
∴点P对应的数是:﹣10点,Q对应的数是:4.
∴4﹣(﹣10)=4+10=14.
∴P、Q两点间的距离为:14个单位长度.
当点P追上点Q时,可得点P与点Q表示的数相同,
∴﹣16+3t=2+t.
∴t=9.
∴﹣16+3t=﹣16+27=11.
∴此时点P对应的数为:11.
∴当t为9时,点P追上点Q,此时点P对应的数为:11.
故答案为:﹣10,14;11.
(3)
解:当Q停止时,所用的时间为4秒,
分四种情况:
当PB=3PA时,
18﹣3t=33t,
解得:t=1.5.
当PA=3PB时,
3t=3(18﹣3t),
解得:t=4.5(舍去).
当AB=3PA时,
18=33t,
解得:t=2.
当AB=3PB时,
18=3(18﹣3t),
解得:t=4.
综上所述:当t为1.5,2或4时,在PA、PB和AB三条线段中,其中一条线段的长度是另一条线段长度的3倍.
【我思故我在】本题考查数轴上两点间的距离,数轴及有理数在数轴上的表示,一元一次方程—行程问题的理解与实际运用能力.一般地,设是一个正数,则数轴上表示数的点在原点的右边,与原点的距离是个单位长度;表示数的点在原点的左边,与原点的距离是个单位长度.数轴上两点之间的距离等于对应两数之差的绝对值.路程速度时间.熟练掌握相关知识点,恰当应用分类思想解决实际问题(行程)是解本题的关键.
8.如图,数轴上的两点A、B所对应的数分别是、6,数轴上有两动点P和Q,点P从点A出发向点B运动,到达点B后立即返回点A,点Q从点B出发向点A运动,点P的运动速度是每秒4个单位,点Q的运动速度是每秒2个单位.点P、Q同时出发,设运动时间为t秒.
(1)数轴上,A、B两点之间的相距_______个单位长度.
(2)当点P从点A向点B运动时,点P所表示的数是_______;在点Q的整个运动过程中,点Q所表示的数是______.(均用含t的代数式表示)
(3)当点P从点A向点B运动时,若P、Q两点在数轴上的点C相遇,求点C所表示的数是多少?
(4)在整个运动过程中,当点Q到原点O的距离是点P到原点O的距离的2倍时,直接写出t的值.
【答案】(1)16;
(2),;
(3);
(4)或或或.
【分析】(1)根据数轴上两点之间的距离求解即可;
(2)根据数轴上的点右加左减的运动特点求解即可;
(3)根据相遇时,P、Q两点走过的路程等于A、B之间的距离列出方程求解即可;
(4)分情况讨论:①当点P从点A向点B运动时,②当点P到达点B返回点A时,表示出求解即可.
(1)
解:∵A、B所对应的数分别是、6,
∴A、B两点之间的相距个单位长度,
故答案为:16
(2)
解:由题意可知:
当点P从点A向点B运动时,经过t秒后,P走过的路程为4t,P在A右侧,故点P所表示的数是;
点Q的运动过程中,经过t秒后,Q走过的路程为2t,Q在B左侧,故点Q所表示的数是;
故答案为:,.
(3)
解:由题意可知:当P和Q相遇时:,
∴,即此时点C表示的数为:.
(4)
解:分两种情况:
①当点P从点A向点B运动时,,
,,
∵,
∴,即或,
解得:或,均符合题意;
②当点P到达点B返回点A时,,
∵,
∴点P所表示的数是,
∴,,
∵,
∴,即或,
解得:或,均符合题意;
综上所述:或或或.
【我思故我在】本题考查数轴上两点之间的距离,数轴上点的表示,一元一次方程的应用,比较复杂,要理解题意,注意数轴上的点,原点左边表示负数,原点右边表示正数,两点之间的距离等于任意两点表示的数的差的绝对值.
【期末满分冲刺】人教版数学七年级上册-专项08《角中的动态综合问题》期末重难点突破: 这是一份【期末满分冲刺】人教版数学七年级上册-专项08《角中的动态综合问题》期末重难点突破,文件包含专项08角中的动态综合问题解析版docx、专项08角中的动态综合问题原卷版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
【期末满分冲刺】人教版数学七年级上册-专项07《古代背景及日历中的方程问题》期末重难点突破: 这是一份【期末满分冲刺】人教版数学七年级上册-专项07《古代背景及日历中的方程问题》期末重难点突破,文件包含专项07古代背景及日历中的方程问题解析版docx、专项07古代背景及日历中的方程问题原卷版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
【期末满分冲刺】人教版数学七年级上册-专项06《商场促销的方程问题》期末重难点突破: 这是一份【期末满分冲刺】人教版数学七年级上册-专项06《商场促销的方程问题》期末重难点突破,文件包含专项06商场促销的方程问题解析版docx、专项06商场促销的方程问题原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












