




【期末满分冲刺】人教版数学七年级上册-专项08《角中的动态综合问题》期末重难点突破
展开专项08 角中的动态综合问题
考点导图
素质拓展
1.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则 t的值为 秒(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,试探索:在旋转过程中,∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
【答案】(1)直线ON平分∠AOC;(2)12或30秒;(3)差为定值30°.
【详解】试题分析:(1)直线ON平分∠AOC,设ON的反向延长线为OD,已知OM平分∠BOC,根据角平分线的定义可得∠MOC=∠MOB,又由OM⊥ON,根据垂直的定义可得∠MOD=∠MON=90°,所以∠COD=∠BON,再根据对顶角相等可得∠AOD=∠BON,即可∴∠COD=∠AOD,结论得证;(1)已知∠BOC=120°,根据平角的定义可得∠AOC=60°,旋转至直线ON恰好平分锐角∠AOC,可得旋转120°或300°时ON平分∠AOC,由此可得10t=120°或300°,所以n=12或30;(3)差为定值30°,因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,再根据角的的和差计算即可.
试题解析:
(1)直线ON平分∠AOC.理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC,即直线ON平分∠AOC.
(2)12或30秒
(3)差为定值30°
∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON、∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.
我思故我在:本题考查了角平分线的定义及角的和差计算,解题的关键是认真审题并仔细观察图形,找到各个量之间的关系.
实战演练
2.如图①,点O为直线AB上一点,射线OC⊥AB于O点,将一直角三角板的60°角的顶点放在点O处,斜边OE在射线OB上,直角顶点D在直线AB的下方.
(1)将图①中的三角板绕点O逆时针旋转至图②,使一边OE在∠BOC的内部,且恰好平分∠BOC,问:直线OD是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线OD恰好平分∠AOC,则t的值为________;(直接写出结果)
(3)将图①中的三角板绕点O顺时针旋转至图③,使OD在∠AOC的内部,请探究:∠AOE与∠DOC之间的数量关系,并说明理由.
【答案】(1)直线OD不平分∠AOC,理由见解析;(2)3或39;(3)∠DOC-∠AOE=30°,理由见解析.
【详解】试题分析:(1)先根据角平分线的性质得到,∠BOE=45°,于是∠BOD=∠DOE-∠BOE=15°,进而求出∠COM与∠AOM的值,∠AOM≠∠COM,直线OD不平分∠AOC;
(2)分OD与OD的延长线平分∠AOC两种情况;
(3)∠AOE=60°-∠AOD、∠DOC=90°-∠AOD,∠DOC-∠AOE=(90°-∠AOD)-(60°-∠AOD)=30°.
试题解析:(1)直线OD不平分∠AOC,理由:因为OE平分∠BOC,所以∠BOE=45°,∠BOD=∠DOE-∠BOE=60°-45°=15°,延长DO至M,则∠COM=180°-90°-15°=75°,∠AOM=90°-75°=15°,即∠AOM≠∠COM;
(2)3或39;
延长DO,
∵∠AOC=90°,
当直线OD恰好平分角∠AOC,
∴∠AOM=∠COM=45°,
即逆时针旋转15°时DO延长线平分∠AOC,
由题意得,5t=15°
∴t=3,
当DO平分∠AOC,
∴∠DOA=45°
即逆时针旋转195°时DO平分∠AOC,
∴5t=195°,
∴t=39,
∴t=3或39;
(3)∠DOC-∠AOE=30°,
∵∠DOE=60°,∠AOC=90°,
∴∠AOE=60°-∠AOD、∠DOC=90°-∠AOD,
∴∠DOC-∠AOE=(90°-∠AOD)-(60°-∠AOD)=30°,
所以∠AOE与∠DOC之间的数量关系为:∠DOC-∠AOE=30°.
3.如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,∠COD=90°;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
【答案】(1)t=8min时,射线OC与OD重合;
(2)当t=2min或t=14min时,射线OC⊥OD;
(3)存在,详见解析.
【分析】(1)当OC与OD重合时,根据角度关系可知∠AOC=∠AOB+∠BOD,利用题中射线的旋转速度,由角度=时间×旋转速度,列出方程,求解即可得到射线OC与OD重合时的时间t;
(2)当∠COD=90°时,可分为两种情况,当OC位于OD的右边时:∠BOD+120°=∠AOC+90°;当OC位于OD左边时:∠AOC-90°-120°=∠BOD,列出对应的方程,求解即可;
(3)分三种情况来考虑,当OB为角平分线时:120°-∠AOC=∠BOD;当OC为角平分线时:∠AOC-120°=∠BOD;当OD为角平分线时:∠AOC-120°=2∠BOD,列方程求解即可.
【详解】解:(1)由题意得,20t=5t+120°,解得t=8,
即当t=8分钟时,射线OC与OD重合;
(2)当OC位于OD的右边时:∠BOD+120°=∠AOC+90°,则可得5t+120°=20t+90°,解得t=2分钟;
当OC位于OD左边时:∠AOC-90°-120°=∠BOD,则可得20t-90°-120°=5t,解得t=14分钟;
故当t=2或14分钟时,∠COD=90°;
(3)存在.
当OB为角平分线时:120°-∠AOC=∠BOD,则可得120°-20t=5t,解得t=4.8分钟;
当OC为角平分线时:∠AOC-120°=∠BOD,则可得20t-120°=×5t,解得t=分钟;
当OD为角平分线时:∠AOC-120°=2∠BOD,则可得20t -120°=2×5t,解得t=12分钟.
故当t=4.8或或12分钟时,射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线.
【我思故我在】本题由角的边的旋转考查了角的和差运算,注意运动的不确定性所带来的多可能性.
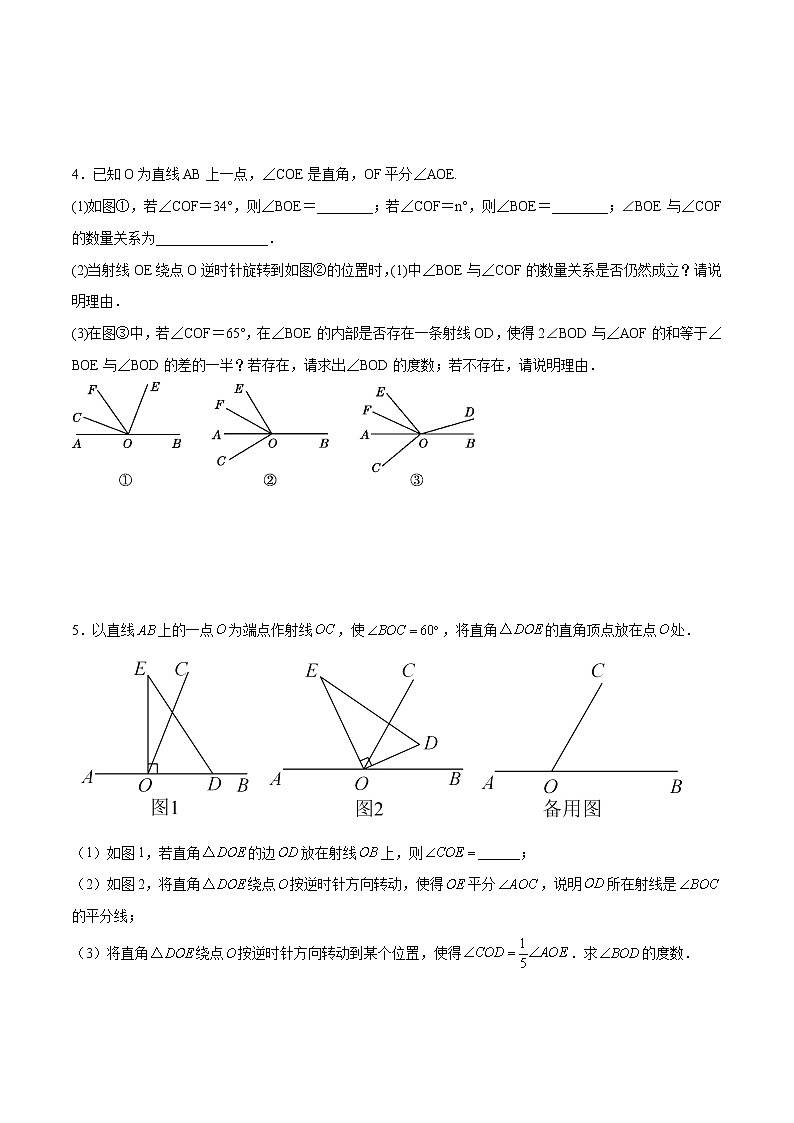
4.已知O为直线AB上一点,∠COE是直角,OF平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=n°,则∠BOE=________;∠BOE与∠COF的数量关系为________________.
(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
(3)在图③中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.
【答案】(1)68°;2n°;∠BOE=2∠COF(2)仍然成立(3)存在
【详解】
(1)若∠COF=34°,则∠BOE=68°;若∠COF=m°,则∠BOE=°;所以∠BOE=2∠COF;
(2)成立.理由如下:
设
∵OF 平分∠AOE
∴ 结合余角和补角的性质,
∴∠BOE=2∠COF;
(3)存在,∠BOD=16°.理由如下:
∵∠COF=65°
∴∠BOE=2∠COF=130°
∴∠AOF=(180°-∠BOE)=25°
又2∠BOD+∠AOF=(∠BOE-∠BOD)
∴2∠BOD+25°=(130°-∠BOD)
∴∠BOD=16°.
考点:角平分线的性质,比较角的大小
点评:解题的关键是熟练掌握角的平分线把角分成相等的两个小角,且都等于大角的一半,注意本题要有整体意识.
5.以直线上的一点为端点作射线,使,将直角的直角顶点放在点处.
(1)如图1,若直角的边放在射线上,则______;
(2)如图2,将直角绕点按逆时针方向转动,使得平分,说明所在射线是的平分线;
(3)将直角绕点按逆时针方向转动到某个位置,使得.求的度数.
【答案】(1)30°;(2)见解析;(3)65°或52.5°
【分析】(1)代入∠BOE=∠COE+∠COB求出即可;
(2)求出∠AOE=∠COE,根据∠DOE=90°求出∠AOE+∠DOB=90°,∠COE+∠COD=90°,推出∠COD=∠DOB,即可得出答案;
(3)画出符合的两种图形,再根据平角等于180°求出即可.
【详解】解:(1)∵∠BOE=∠COE+∠COB=90°,
又∵∠COB=60°,
∴∠COE=30°,
故答案为:30;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=∠COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x,则∠AOE=5x.
有两种情况:①如图1,OD在∠AOC内部时,
∵∠AOE+∠DOE+∠COD+∠BOC=180°,∠DOE=90°,∠BOC=60°,
∴5x+90°+x+60°=180°,
解得x=5°,
即∠COD=5°.
∴∠BOD=∠COD+∠BOC=5°+60°=65°;
②如图2,OD在∠BOC的内部时,如图2,
∵∠AOC+∠BOC=180°,∠DOE=90°,∠BOC=60°,∠COD=x°,∠AOE=5x°,
∴5x+90-x+60=180,
解得:x=7.5,
即∠COD=7.5°,
∵∠BOC=60°,
∴∠BOD=60°-7.5°=52.5°,
∴∠BOD的度数为65°或52.5°.
【我思故我在】本题考查了角平分线定义和角的计算,能根据图形和已知求出各个角的度数是解此题的关键.
6.已知:,OB、OM、ON,是 内的射线.
(1)如图 1,若 OM 平分 , ON平分.当射线OB 绕点O 在 内旋转时,= 度.
(2)OC也是内的射线,如图2,若 ,OM平分,ON平分,当射线OB绕点O在内旋转时,求的大小.
(3)在(2)的条件下,当射线OB从边OA开始绕O点以每秒的速度逆时针旋转t秒,如图3,若,求t的值.
【答案】(1)80;(2)70°;(3)26
【分析】(1)根据角平分线的定义进行角的计算即可;
(2)依据OM平分∠AOC,ON平分∠BOD,即可得到∠MOC=∠AOC,∠BON=∠BOD,再根据∠MON=∠MOC+∠BON-∠BOC进行计算即可;
(3)依据∠AOM=(10°+2t+20°),∠DON=(160°-10°-2t),∠AOM:∠DON=2:3,即可得到3(30°+2t)=2(150°-2t),进而得出t的值.
【详解】解:(1)∵∠AOD=160°,OM平分∠AOB,ON平分∠BOD,
∴∠MOB=∠AOB,∠BON=∠BOD,
∴∠MON=∠MOB+∠BON=∠AOB+∠BOD=(∠AOB+∠BOD)=∠AOD=80°,
故答案为:80;
(2)∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=∠AOC,∠BON=∠BOD,
∴∠MON=∠MOC+∠BON-∠BOC
=∠AOC+∠BOD-∠BOC
=(∠AOC+∠BOD)-∠BOC
=×180-20
=70°;
(3)∵∠AOM=(2t+20°),∠DON=(160°-2t),
又∠AOM:∠DON=2:3,
∴3(20°+2t)=2(160°-2t)
解得,t=26.
答:t为26秒.
【我思故我在】本题考查的是角平分线的定义和角的计算,从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线,解决本题的关键是理解动点运动情况.
7.一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
【发现猜想】(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.
【探索归纳】(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
【问题解决】(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
【答案】(1)85°;(2)∠AOC=;理由见解析;(3)经过,,4秒时,其中一条射线是另外两条射线夹角的平分线.
【分析】(1)根据∠AOD、∠AOB、∠BOD之间的关系,求出∠BOD的度数,然后根据角平分线的性质算出∠BOC的度数,再计算∠AOC即可解决问题.
(2)根据∠AOD、∠AOB、∠BOD之间的关系,用m、n表示出∠BOD的度数,然后根据角平分线的性质用m、n的代数式表示出∠BOC,最后再表示出∠AOC即可解决问题.
(3)根据各角之间存在的数量关系,设经过x秒时,分别用x将∠DOA、∠COA、∠BOA表示出来,然后分四类情况讨论,根据角平分线的性质列出方程,解决即可.
【详解】(1)85°;
(2)∵∠AOB=m,∠AOD=n
∴∠BOD=n-m
∵OC为∠BOD的角平分线
∴∠BOC=
∴∠AOC=+m=
(3)设经过的时间为x秒,
则∠DOA=120°-30x;∠COA=90°-10x;∠BOA=20°+20x;
①当在x=之前,OC为OB,OD的角平分线;30-20x=70-30x,x1=4(舍);
②当x在和2之间,OD为OC,OB的角平分线;-30+20x=100-50x,x2=;
③当x在2和之间,OB为OC,OD的角平分线;70-30x=-100+50x,x3=;
④当x在和4之间,OC为OB,OD的角平分线;-70+30x=-30+20x,x4=4.
答:经过,,4秒时,其中一条射线是另外两条射线夹角的平分线.
【我思故我在】本题考查了角平分线的性质,一元一次方程的应用,解决本题的关键是熟练掌握角平分线的性质,理清各个角之间存在的数量关系,根据数量关系列出方程.
8.点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.
【答案】(1) 130°;(2)t=3或11.4;(3)t=4.5或或9或
【分析】(1)分别求出∠AOM和∠BON的度数,即可得出答案;
(2)分为两种情况,得出方程10t+15t=180-105或10t+15t=180+105,求出方程的解即可;
(3)分为四种情况,列出方程,求出方程的解即可.
【详解】(1)当t=2时,∠AOM=10°t=20°,∠BON=15°t=30°,
所以∠AOB=180°﹣∠AOM﹣∠BON=130°;
(2)当∠AOB=105°时,有两种情况:
①10t+15t=180﹣105,解得:t=3;
②10t+15t=180+105,解得:t=11.4;
(3)①当OB是∠AON的角平分线时,10t+15t+15t=180,解得:t=4.5;
②当OA是∠BOM的角平分线时,10t+10t+15t=180,解得:t=;
③当OB是∠AOM的角平分线时,5t+15t=180,解得:t=9;
④当OA是∠BON的角平分线时,10t+7.5t=180,解得:t=.
【我思故我在】本题考查了角平分线的定义和邻补角的定义,能求出符合的所有情况是解此题的关键.
9.多多对几何中角平分线等兴趣浓厚,请你和多多一起探究下面问题吧.已知∠AOB=100°,射线OE,OF分别是∠AOC和∠COB的角平分线.
(1)如图1,若射线OC在∠AOB的内部,且∠AOC=30°,求∠EOF的度数;
(2)如图2,若射线OC在∠AOB的内部绕点O旋转,则∠EOF的度数_____;
(3)若射线OC在∠AOB的外部绕点O旋转(旋转中∠AOC,∠BOC均指小于180°的角),其余条件不变,请借助图3探究∠EOF的大小,请直接写出∠EOF的度数(不写探究过程).
【答案】(1)
(2)
(3)或
【分析】(1)先根据角平分线的定义可得,再根据角的和差、角平分线的定义可得,然后根据即可得;
(2)先根据角的和差可得,再根据角平分线的定义可得,然后根据即可得;
(3)如图(见解析),先根据角平分线的定义可得,再分①射线在的内部,②射线在的内部,③射线在的内部三种情况,分别根据角的和差即可得.
(1)
解: 是的平分线,,
,
,
,
是的平分线,
,
;
(2)
,
,
是的平分线,是的平分线,
,
故答案为:
(3)
是的平分线,是的平分线,
,
由题意,分以下三种情况:
①如图,延长至点,当射线在的内部时,
,
,
;
②如图,延长至点,延长至点,当射线在的内部时,
,
,
;
③如图,延长至点,当射线在的内部时,
,
,
;
综上,的度数为或.
【我思故我在】本题考查了角平分线的定义、角的和差等知识点,较难的是题(3),正确分三种情况讨论是解题关键.
10.如图,已知直线和交于点,,,垂足为,平分.
(1)当时,则______;______;
(2)当时,射线从开始绕点逆时针匀速转动,同时,射线从开始绕点匀速转动,且射线的转动速度大于射线的转动速度.
①若射线顺时针转动,则射线与射线经过7.5秒第一次重合;若射线逆时针转动,则射线与射线经过37.5秒第一次重合.求射线,绕点转动的速度分别是多少?
②若射线,绕点转动的速度与①中转动速度相同,射线顺时针转动,当射线转动一周时,射线也停止转动,当时,直接写出射线转动的时间.
【答案】(1)60°,75°
(2)①射线绕点转动的速度是,射线绕点转动的速度是;②射线转动的时间为3或12或21或30.
【分析】(1)利用互余可知,利用互补及角平分线的性质可知;
(2)①先根据,可知,则两种情况可以类比二元一次方程应用中的路程问题,根据相遇、追击两种情况列出方程组,求解即可;
②分两种情况:在直线0E的左边和右边,根据其夹角列4个方程可得时间.
(1)
解:∵,
∴,
∵,
∴,
∵,
∴,
∵平分,
∴,
故答案为:60°,75°;
(2)
①设射线绕点转动的速度是,射线绕点转动的速度是,
由题意列方程组为,
解得,
答:射线绕点转动的速度是,射线绕点转动的速度是;
②设射线转动的时间为t秒,
由题意得:或或或,
解得:或或或,
综上所述:射线转动的时间为3或12或21或30.
【我思故我在】本题考查了对顶角相等,邻补角互补的定义,解二元一次方程组,角平分线的定义,角的计算,第二问有难度,难点在于要分情况讨论.
【期末满分冲刺】人教版数学八年级上册-专题06《整式乘除的综合问题》期末重难点突破: 这是一份【期末满分冲刺】人教版数学八年级上册-专题06《整式乘除的综合问题》期末重难点突破,文件包含专题06整式乘除的综合问题解析版docx、专题06整式乘除的综合问题原卷版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
【期末满分冲刺】人教版数学七年级上册-专项07《古代背景及日历中的方程问题》期末重难点突破: 这是一份【期末满分冲刺】人教版数学七年级上册-专项07《古代背景及日历中的方程问题》期末重难点突破,文件包含专项07古代背景及日历中的方程问题解析版docx、专项07古代背景及日历中的方程问题原卷版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
【期末满分冲刺】人教版数学七年级上册-专项06《商场促销的方程问题》期末重难点突破: 这是一份【期末满分冲刺】人教版数学七年级上册-专项06《商场促销的方程问题》期末重难点突破,文件包含专项06商场促销的方程问题解析版docx、专项06商场促销的方程问题原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












